給學生插上想象的翅膀

趙芳

摘要：數學課堂以學生主動探索、發現、獲取知識為目的，教師不只是教學生知識，更要教會學生自主學習、合作交流和掌握學習的方法，讓學生在課堂中充滿想象，使學生的積極性及靈感得到充分發揮。

關鍵詞：數學課堂；提高；想象力

中圖分類號：G633.6 文獻標識碼：A 文章編號：1992-7711（2016）01-0091

筆者在看了一個故事“聰明人”之后，深受感觸。故事的內容是：

華生跟著福爾摩斯多年，也變得越來越聰明。一天晚上，他們在野外搭起帳篷睡覺。半夜里，華生被福爾摩斯推醒。“華生，你看看天上，告訴我，你發現了什么？”

“我看到滿天的星星。”華生說。“那么，你有什么發現？”華生想了想，然后答道：“從天文學上講，這說明天上有數以萬計的星系，還可能有數以億計的行星；從占星術上講，這說明土星在獅子座；從測時法上來說，這說明現在的時間是夜里三點半左右；從氣象學上來說，明天應該是晴朗的一天；從神學上來說，這說明我們在上帝面前非常渺小。福爾摩斯，你看我的推理如何？”福爾摩斯大聲喊道：“華生，你難道沒有看出來我們的帳篷被偷了嗎！”

從這個故事中，讓筆者領悟到，有時放開學生的思維，讓學生各抒己見，即使學生的回答無法涉及到你的課堂預設要求，只要我們給予他們發言的機會和時間，多方位、多角度迸發出學生的各種思維火苗。

現在我們一直強調上課要“以學為中心”，究竟什么是“以學為中心”？筆者認為可以從三個角度去理解，一是課堂上強調學生自主學習的主動性，給予學生的知識不再是被動地死記，而是激發學生對學習知識的興趣和探究新知的基礎上，讓學生自主探索、積極靈活地掌握知識、融會貫通。二是教師要主動鉆研教材，把握每節課的重點、難點，深入簡出地加以講透、講深和講精。讓不同層次的學生在每節課上都有收獲。三是教師帶領學生從已有知識入手，深挖知識內涵，進一步探索新知識，真正體會數學課堂的精髓——學為所用。下面，筆者就從三個方面分析與闡述。

一、會做更要會想

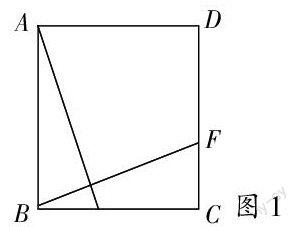
古人云：“授之以魚，不如授之與漁。”體現了教是為了不教，教會科學知識不如培養科學素質的理念。由于數學這一學科的靈活性，為聰明學生所不以為然，又由于它的綜合性，又使中學生所畏難。如筆者在一節“正方形的性質”中講到一題：已知：如圖，在正方形ABCD中，E，F分別是BC，CD上的點，

求證：AE=BF。

由于學生被思維定勢，認為只要教師出的題目，一定能解答，結果由于缺少一個條件。然后讓學生自己添加一個條件，做出結論，結果有八種添法。這一道題，每位學生都積極參與，哪怕平時很少發言的學生，也積極地舉起手來，想要發表自己的觀點，這時，教師應該給予他們展示的機會，讓他們找回自信，一旦他們答錯了，也要耐心而仔細地給予講解，平等地對待他們，用教師自己的人格力量推動他們前進。

二、引領更要點睛

一味地追求課堂師生雙邊活動的開展，做一些與數學理念無關的小游戲，純粹是浪費學生的時間。要分析問題要素，要教學生解決問題，必須先教學生分析問題的要素，幫助他們正確分析問題的癥結所在，采用正確的解決方法。

給孩子講作業時，碰到“將棱長是1.6分米的正方體石塊浸沒到一個長方體水槽里，水面上升了4.8分米，然后放入一個鐵塊并浸沒，水面又上升了0.9分米，求鐵塊的體積。”

講前自己認為已經做好了充分準備，但在開講時，仍然找不到如何讓孩子去真正的理解這個數學問題，于是想到了直觀的實驗。拿一個長方體水槽做實驗，結果孩子弄得一頭霧水，仍然不清楚這個數學問題的突破口，最后，打算把這個問題進行簡單化，逐步把難點一個個突破和解決。筆者編一題“長方體水槽的底面積為6平方分米，將一個正方體石塊浸沒到長方體水槽里，水面上升了2分米，求這個正方體體積。”孩子一下就列出算式，找到正確答案。于是乘勝追擊，“將棱長為2分米的正方體石塊浸沒到一個長方體水槽里，水面上升了4分米，求這個長方體水槽的底面積。”孩子又一次輕而易舉的得到答案。小結一下，其實根據“浸沒在水槽里的正方體體積就是水面上升部分的體積。”所以，上題中只要得到長方體水槽的底面積，就可以求出鐵塊的體積。把問題中的難點講明講透，孩子樂意做這種題目，強烈要求筆者再編幾題進行實踐。

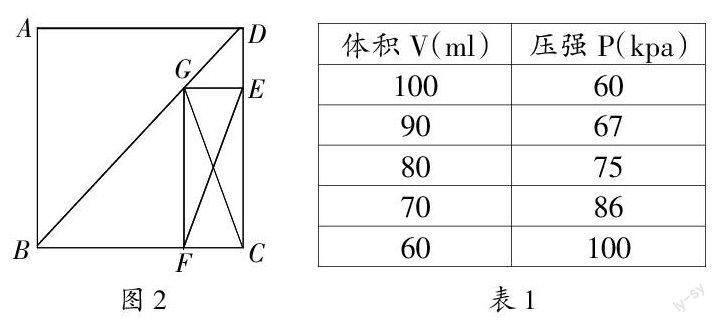
從這個事實中，筆者想到在課堂上，把問題中的難點一一加以細化，學生也會積極配合，樂于做數學。于是，在上“正方體”一節，有一道例題：已知：如圖，在正方體ABCD中，G是對角線BD上的一點，GE⊥CD，GF⊥BC，E，F分別為垂足，連結AG，EF。求證：AG=EF。這題的難點是添輔助線，學生不易想到，但提醒學生，正方體是以對角線所在直線為對稱軸，G是正方形一條對角線上的一點，即G是對稱軸上的點，且A點與C點是對稱點，那么，不難發現線段AG與線段CG相等。通過找相等線段的轉化思想，學生一下找到解決問題的方法。

又如，在八年級的浙教版數學下冊《6.3 反比例函數的應用》一節，講到例2：在溫度不變的條件下，通過一次又一次地對汽缸頂部的活塞加壓，測出每一次加壓后汽缸內氣體的體積和氣體對汽缸壁所產生的壓強。求根據表中的數據求出壓強關于體積的函數表達式。這個例題，教學中要充分展現探究過程，作為教師要讓學生根據表格中給出的實驗數據，將作怎樣的分析、處理？首先給學生充分的時間，讓學生自己探索。有的學生仔細觀察表格數據后，發現數據之間的聯系，會得到“并列兩個數的乘積為相同的常數”，但只占全班的百分之十，教師在肯定這一小部分學生的同時，正確引導目前還得不到答案的學生再從作圖進行分析，大部分學生自然會通過直角坐標系進行畫圖，然后按照自變量從小到大排列連接成一條線，這條線讓學生仔細觀察是什么形狀。問題的解決自然水到渠成。

上課之前，教師要善于動腦，為學生解決難題找突破口，甚至可以作鋪墊。教師把問題講透講明，學生就會樂于去做題目、樂于去學習所謂枯燥的數學。

三、挖掘更要創新

教材是知識的載體，是師生教與學的中介，它只是提供了學生學習活動的基本材料，它需要我們發揮創造才能去豐富和完善，挖掘教材趣味性的資源，吸引學生，才會激發起學生的創新才能。美國教育家布魯納說過：“學習的最好動力是對學習材料的興趣。”趣味性的材料，不但能激發學生的興趣，而且能使他們產生新奇的創意，因此在數學教學中，我們應立足于教材的知識點，挖掘教材的趣味性，引導學生從多角度去看、去想、去說，多方面釋放學生思維，放飛學生的想象，誘發其創意潛能。

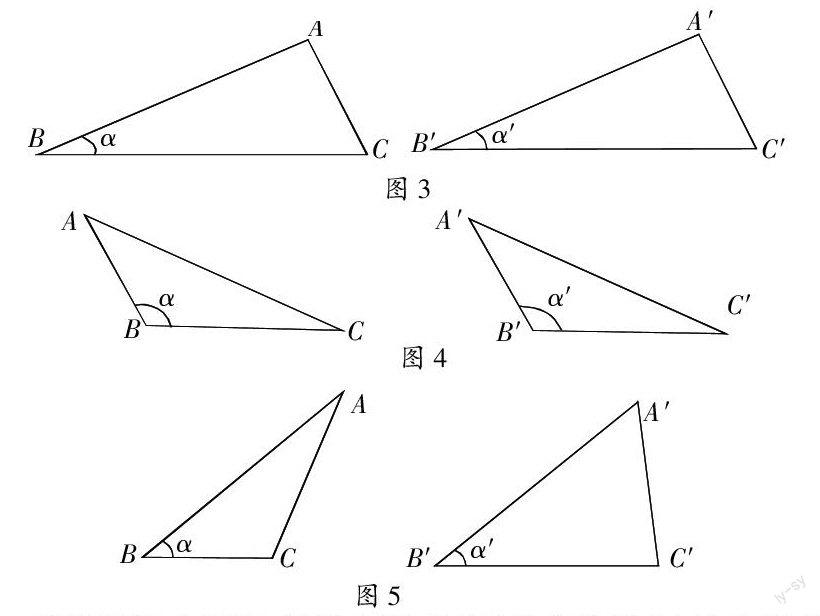
在八年級上冊《直角三角形的全等》中，直角三角形全等除了“SSS，SAS，ASA，AAS”這四種方法之外，還有“HL”定理。對于證明，學生自然會想到結合勾股定理，轉化為‘SSS判定方法進行證明。這樣講解似乎已經把“HL”定理講明講透了，學生能夠接受。其實，筆者認為還只是把課本的內容搬給學生而已，真正要讓學生弄清楚這一定理，必須與《三角形全等》中的“SAS”聯系比較。因為講“SAS”時，教師強調這里的“A”指“兩邊的夾角”，但“HL”定理也可以貌似于“SSA”，為什么這時的“兩邊及一邊所對的角相等的兩個三角形全等”成立。如下列三個組合中AB=A′B′，∠α=∠α′，愛思考的學生就會提出這一現象。作為教師要提供給孩子一粒帶芽的種子，給他們提示，當一邊所對的角都是銳角，都是鈍角，都可以得到兩個三角形全等，但若所對的角一個是銳角，另一個是鈍角，那么這兩個不全等。

這樣的學習、質疑，給學生留下“懸念”，激發學生創新思維的發展。巴爾扎克說過：“打開一切科學的鑰匙都毫無異議地是問號。”學生善于發現問題并能提出自己的意見，特別是帶有創造性的見解，是極其可貴的，一個在學習中畏手畏腳，不敢提出問題，墨守成規的學生是不會有創新精神的。

引導學生積極思考、善于質疑、大膽發問，使教學出現觀點的交鋒，智慧的碰撞，進而迸發出創新的火花，這是發展學生創造思維的一把金鑰匙。總之，學生的創新潛能好比一個礦，這個礦里面藏著很豐富的礦產，它需要人們去勘探、發現和開采。如果把它永遠埋在地下，就不能成為有用的資源。這就需要我們教師在數學課堂教學中，努力培養學生的創新意識，挖掘學生的創新潛能，才能培養出大批具有創新精神的人才。

（作者單位：浙江省紹興市上虞區上浦鎮中學 312000）