數(shù)形結(jié)合：開(kāi)啟小學(xué)數(shù)學(xué)數(shù)與計(jì)算教學(xué)的金鑰匙

童永安

（江西省九江市永修縣建昌小學(xué) 江西九江 330300）

?

數(shù)形結(jié)合：開(kāi)啟小學(xué)數(shù)學(xué)數(shù)與計(jì)算教學(xué)的金鑰匙

童永安

（江西省九江市永修縣建昌小學(xué) 江西九江 330300）

摘 要：學(xué)生體會(huì)數(shù)學(xué)思想是其數(shù)學(xué)思維能力發(fā)展的關(guān)鍵，數(shù)學(xué)思想方法是數(shù)學(xué)教學(xué)的靈魂。用數(shù)形結(jié)合方法可以使復(fù)雜問(wèn)題簡(jiǎn)單化、抽象問(wèn)題具體化；能夠變抽象的數(shù)學(xué)語(yǔ)言為直觀的圖形、抽象思維為形象思維，有助于把握數(shù)學(xué)問(wèn)題的本質(zhì)，數(shù)形結(jié)合是開(kāi)啟教學(xué)智慧的鑰匙。在小學(xué)數(shù)學(xué)數(shù)與計(jì)算教學(xué)中運(yùn)用數(shù)形結(jié)合思想方法，發(fā)展學(xué)生數(shù)感，培養(yǎng)學(xué)生估算，理解概念，突破算理，理清數(shù)量關(guān)系，解決問(wèn)題，使教學(xué)收到事半功倍的效果。

關(guān)鍵詞：數(shù)形結(jié)合 數(shù)與計(jì)算教學(xué) 思想 方法

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011版）》明確指出，數(shù)學(xué)的學(xué)習(xí)不僅僅是學(xué)習(xí)數(shù)學(xué)基本知識(shí)和技能，還包括數(shù)學(xué)基本思想和基本活動(dòng)經(jīng)驗(yàn)的積累，強(qiáng)調(diào)學(xué)生經(jīng)歷知識(shí)的自主探究過(guò)程，在知識(shí)的形成過(guò)程中感悟和體會(huì)數(shù)學(xué)思想。學(xué)生體會(huì)數(shù)學(xué)思想是其數(shù)學(xué)思維能力發(fā)展的關(guān)鍵。

小學(xué)數(shù)學(xué)教材是數(shù)學(xué)教學(xué)的顯性知識(shí)系統(tǒng)，數(shù)學(xué)思想方法是數(shù)學(xué)教學(xué)的靈魂。小學(xué)數(shù)學(xué)中常見(jiàn)的數(shù)學(xué)思想方法有：對(duì)應(yīng)、數(shù)形結(jié)合、假設(shè)、猜想、列舉、推理、轉(zhuǎn)化、比較、分析、綜合、歸納、演繹、集合、符號(hào)、抽象概括等。用數(shù)形結(jié)合方法可以使復(fù)雜問(wèn)題簡(jiǎn)單化、抽象問(wèn)題具體化；能夠變抽象的數(shù)學(xué)語(yǔ)言為直觀的圖形、抽象思維為形象思維，有助于把握數(shù)學(xué)問(wèn)題的本質(zhì)。數(shù)形結(jié)合是解決數(shù)學(xué)問(wèn)題常用的思想方法，是直觀與抽象，感知與思維的結(jié)合。可以說(shuō)數(shù)形結(jié)合是開(kāi)啟教學(xué)智慧的鑰匙。

下面具體談?wù)剶?shù)形結(jié)合思想在小學(xué)數(shù)學(xué)數(shù)與計(jì)算教學(xué)中的運(yùn)用。

“數(shù)與代數(shù)”的主要內(nèi)容有：數(shù)的認(rèn)識(shí)，數(shù)的表示，數(shù)的大小，數(shù)的運(yùn)算，數(shù)量的估計(jì)；字母表示數(shù)，代數(shù)式及其運(yùn)算；方程、方程組、不等式、函數(shù)等。對(duì)這些極為抽象的數(shù)學(xué)語(yǔ)言、數(shù)學(xué)內(nèi)容的教學(xué)，可利用“數(shù)形結(jié)合”思想設(shè)計(jì)教學(xué)活動(dòng)，為學(xué)生提供恰當(dāng)?shù)男蜗蟛牧希瑢⒊橄蟮臄?shù)量關(guān)系具體化，把隱性的數(shù)學(xué)本質(zhì)顯性化，使教學(xué)收到事半功倍的效果。

一、數(shù)形結(jié)合，發(fā)展學(xué)生數(shù)感

在學(xué)習(xí)中通常以直尺為原型，逐步經(jīng)歷從“數(shù)尺”到“數(shù)線”再到“數(shù)軸”的過(guò)程，把數(shù)與“數(shù)軸”的點(diǎn)一一對(duì)應(yīng)起來(lái)，數(shù)可以視為點(diǎn)，點(diǎn)可以視為數(shù)，幫助學(xué)生理解數(shù)的意義、順序和大小。

在教學(xué)“負(fù)數(shù)的大小比較”時(shí)，我在數(shù)軸上表示出正數(shù)和負(fù)數(shù)的排列順序。

引導(dǎo)學(xué)生觀察“0”在數(shù)軸上的特殊位置，以“0”為分界點(diǎn)，“0”的右邊是正數(shù)，從左往右依次排列，越來(lái)越大；“0”的左邊是負(fù)數(shù)，從右往左依次排列，越來(lái)越小。借助數(shù)軸形象感知數(shù)軸上的數(shù)從左往右的順序就是從小到大的順序，比“0”大的數(shù)是正數(shù)，比“0”小的數(shù)是負(fù)數(shù)，“0”既不是正數(shù)也不是負(fù)數(shù)，實(shí)現(xiàn)對(duì)數(shù)的結(jié)構(gòu)的整體建構(gòu)。

二、數(shù)形結(jié)合，培養(yǎng)學(xué)生估算

在教學(xué)抽象的“數(shù)”時(shí)，往往要借助于直觀的“形”，利用數(shù)形結(jié)合方法能使‘?dāng)?shù)”和“形”統(tǒng)一起來(lái)，豐富學(xué)生對(duì)數(shù)的形象感知，進(jìn)一步發(fā)展學(xué)生的數(shù)感。

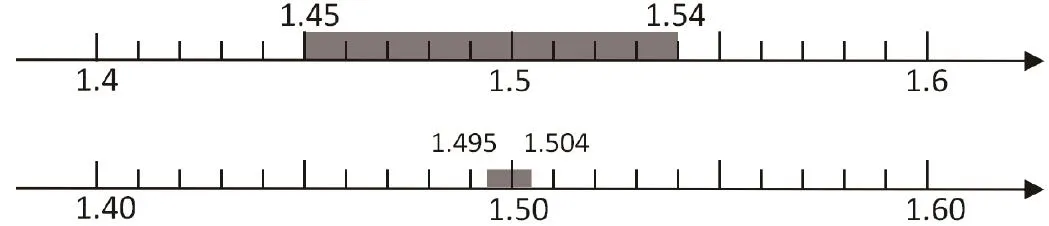
如教學(xué)《求一個(gè)小數(shù)的近似數(shù)》時(shí)，為了突破教學(xué)難點(diǎn)“區(qū)別近似數(shù)1.5和1.50，理解保留的小數(shù)位數(shù)越多，求出的近似值越精確”，我就設(shè)計(jì)了如下數(shù)軸：

由于數(shù)軸實(shí)現(xiàn)了數(shù)與形的聯(lián)系，將數(shù)與直線上的點(diǎn)建立了對(duì)應(yīng)關(guān)系，揭示了數(shù)與形的內(nèi)在關(guān)系，從而使抽象的數(shù)有“形”可依。通過(guò)借助數(shù)軸對(duì)比，讓學(xué)生直觀感受到近似數(shù)是1.5的兩位小數(shù)在1.45～l.54之間，而近似數(shù)是1.50的三位小數(shù)在1.495～1.504之間，范圍小了，所以1.50比1.5更精確。之后又追問(wèn)：近似數(shù)是1.500的四位小數(shù)的范圍呢？近似數(shù)是1.5000的呢？拓展思維，并滲透了極限思想，學(xué)生能感受到保留的小數(shù)位數(shù)越多，近似數(shù)的精確度越高，也就破解本節(jié)課的教學(xué)難點(diǎn)。

三、數(shù)形結(jié)合，理解概念

“倍”的學(xué)習(xí)使三年級(jí)小學(xué)生的認(rèn)知結(jié)構(gòu)發(fā)生“質(zhì)”的變化，因此小學(xué)生學(xué)習(xí)“倍”的知識(shí)感覺(jué)非常困難。我在教學(xué)時(shí)讓學(xué)生在操作的基礎(chǔ)上充分利用數(shù)形結(jié)合，建構(gòu)倍的直觀模型，以突破這個(gè)教學(xué)難點(diǎn)。通過(guò)感官操作，將圖案與具體實(shí)物間建立一一對(duì)應(yīng)的關(guān)系，使學(xué)生清楚地看到比較量有幾個(gè)標(biāo)準(zhǔn)，就是標(biāo)準(zhǔn)量的幾倍，從而由已有知識(shí)認(rèn)識(shí)“倍”的數(shù)學(xué)概念。數(shù)形結(jié)合在這里體現(xiàn)的是數(shù)量與圖形之間的對(duì)應(yīng)關(guān)系，引導(dǎo)學(xué)生通過(guò)數(shù)與圖的相互轉(zhuǎn)化來(lái)明確兩個(gè)比較量之間的數(shù)量關(guān)系，使他們很快就觸及概念的本質(zhì)。

四、數(shù)形結(jié)合，突破算理

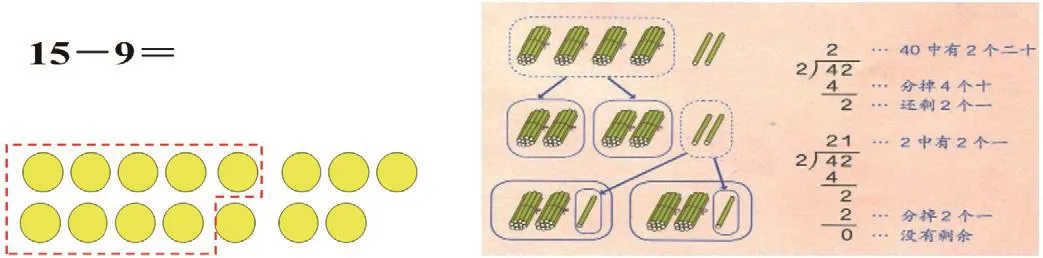
數(shù)的運(yùn)算是“數(shù)與代數(shù)”部分的重要內(nèi)容，也是整個(gè)小學(xué)階段數(shù)學(xué)學(xué)習(xí)的基礎(chǔ)，可以說(shuō)計(jì)算貫穿學(xué)生整個(gè)小學(xué)階段數(shù)學(xué)學(xué)習(xí)的始終。小學(xué)生在低年級(jí)主要以形象思維為主，由于這一思維特點(diǎn)，學(xué)生在開(kāi)始接觸計(jì)算時(shí)，是很難理解其中的算法和算理的，其往往通過(guò)數(shù)形結(jié)合來(lái)理解算理。如學(xué)生在學(xué)習(xí)退位減法時(shí)，學(xué)生需要借助圖形來(lái)理解其中的意義，如下圖，15 -9這一退位減法中，學(xué)生借助圖形來(lái)理解算式的意義，其中的算理在圖形中也一目了然。再如下圖，人教版三年級(jí)下冊(cè)學(xué)習(xí)筆算除法時(shí)，教材在處理42÷2時(shí)，首先借助于42根小棒分成兩堆的圖示分解來(lái)幫助學(xué)生理解42÷2的意義，在此基礎(chǔ)上再引入短除法，結(jié)合圖形來(lái)學(xué)習(xí)短除法，數(shù)形結(jié)合理解其中的算理。

五、數(shù)形結(jié)合，理清數(shù)量關(guān)系，解決問(wèn)題

中低年級(jí)學(xué)生的分析和理解能力尚淺，更需要借助數(shù)形結(jié)合的方法，化繁瑣為簡(jiǎn)單，變易錯(cuò)為準(zhǔn)確，找準(zhǔn)數(shù)量間的關(guān)系，從而正

確解決問(wèn)題。例如，解決行程問(wèn)題時(shí)，常用畫(huà)線段圖、標(biāo)數(shù)據(jù)來(lái)分析、理解題意，找到解決問(wèn)題的方法。

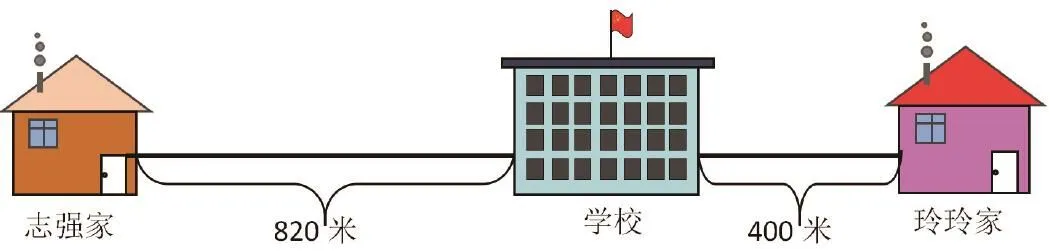
志強(qiáng)中午不回家，在學(xué)校吃飯；玲玲中午回家吃飯。每天上學(xué)和回家，誰(shuí)走的路多些？先估一估，再算一算。

教師先讓學(xué)生讀題、理解題意，能正確指出小華、小蕓每天上學(xué)和回家各走的路程，然后在師生問(wèn)答互動(dòng)中完成簡(jiǎn)潔的線段圖。如下：

借助直觀、形象的線段圖，學(xué)生很快理清數(shù)量關(guān)系，找到解決問(wèn)題的方法。

華羅庚先生說(shuō)過(guò)：“數(shù)與形，本是相倚依，焉能分作兩邊飛。數(shù)無(wú)形時(shí)少直覺(jué)，形少數(shù)時(shí)難入微。數(shù)形結(jié)合百般好，隔離分家萬(wàn)事非；切莫忘，幾何代數(shù)統(tǒng)一體，永遠(yuǎn)聯(lián)系，切莫分離！”這里明確指出了數(shù)形結(jié)合的價(jià)值，并揭示了數(shù)形結(jié)合的本質(zhì)。數(shù)形結(jié)合既是一種重要的數(shù)學(xué)思想，也是一種智慧的教學(xué)方法。在小學(xué)數(shù)學(xué)教學(xué)中，教師應(yīng)該有計(jì)劃、有意識(shí)、有步驟地滲透數(shù)形結(jié)合思想的教學(xué)，使學(xué)生逐步接受數(shù)形結(jié)合思想，并使之成為學(xué)習(xí)數(shù)學(xué)、解決數(shù)學(xué)問(wèn)題的工具。

引用：

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》北京師范大學(xué)出版社2012年1月第一版ISBN978-7-303-13310-9；

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）解讀》北京師范大學(xué)出版社2012年1月第一版ISBN978-7-303-13883-8；