小學數學解決問題策略的案例分析與研究
于德鋒
摘 要:“問題解決”是近年來國際上提出的數學教育的研究熱點,其教學思想自 1980年由美國人提出后,在國際數學教育界受到普遍重視。就數學教育而言,“問題解決”就是在教學中貫徹創造性地應用數學以解決問題的思想,讓學生的學習變為學會思維的活動過程。或者說“問題解決”教學是一個發現、探究和創新的過程。
關鍵詞:小學數學;解決問題;策略
中圖分類號:G622 文獻標識碼:B 文章編號:1002-7661(2016)11-115-02
解決問題的價值不只是獲得具體問題的解,更多的是學生在解決問題過程中獲得的發展。其中主要的一點,在于使學生學習一些解決問題的基本策略,體驗解決問題策略的多樣性,并在此基礎上形成自己解決問題的某些策略。通過分析學生解決問題過程中,本研究在進行文獻分析和比較的情況下,認為經常用到的一些策略有以下幾項:
一、猜想
猜想,就是先猜一猜,再嘗試進行驗證。如,在下面算式的□中填入六個質數,使算式成立。(當然,猜想時學生首先要知道什么是質數,用質數填空,每一個數字最大不超過10,即10以內的質數2、3、5、7。)
根據題目要求,學生首先想到第二個加數的個位分別可填2、3、5,但是得到的和的個位數都不是質數,于是填寫7。7+6=13,個位是3,是一個質數,符合要求。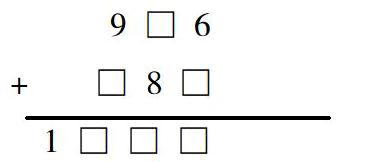
第二步嘗試,第一個加數的十位數填2,加上8及進位1, 2+8+1=11,11的個位數不是質數,因此改為填3,經檢驗,和的十位數為2,是個質數,符合要求。填5或者7,檢驗和的個位都不是質數,因此只能填3。
接下來考慮,第二個加數的百位數。如果填2,再加進位1,9+2+1=12,個位2符合要求;如果填3,再加進位1,9+3+1=13,個位3也符合要求;如果填5,再加進位1,9+5+1=15,個位5也符合要求;如果填7,再加進位1,9+7+1=17,個位7也符合要求;因此,第二個加數的百位數可以填2、3、5、7四種。
經過嘗試和檢驗,發現這道題可以有四種答案。見下面答案:
二、畫圖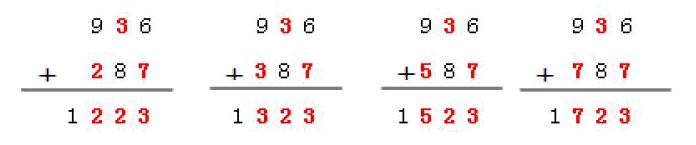
小學生由于年齡局限,對于符號、運算性質等的推理可能會有一些困難,適時的讓他們在本上畫一畫,可以拓展學生解決問題的思路,幫助他們找到解決問題的關鍵。通過畫圖能夠把一些抽象的數學問題具體化,復雜的問題簡單化。
對于條件開放的題目,小學生常常容易被迷惑,以為只有一種答案。實際上有的題目不止一種情況,答案也會有好幾種。如下題:
甲乙兩人分別從公路上的A、B兩處同時出發,相向而行。如果甲每秒鐘走1米,乙每秒鐘走0.8米,10分鐘后兩人相距50米。求A、B兩處相距多少米?
四、置換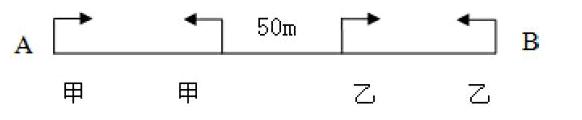
置換就是把兩種或者兩種以上的不同物體統一為一種物體,即用一種事物代替另一種事物,借以簡化題意。如下題:學校買來360個羽毛球,分別裝在4個大盒和4個小盒里,如果每個大盒同2個小盒裝的同樣多。問:每個大盒與小盒各裝多少個羽毛球?
思考:可以把其中的一種盒子置換成另一種盒子,如2個小的等于1個大的;4個小的等于2個大的;這樣原題就可以簡化為:把360個羽毛球可以裝在6個大盒中或者12個小盒中。因此1個大盒可裝360÷6=60(個),1個小盒可裝360÷12=30(個)。
五、逆推
逆推,也叫反推或者還原,就是從反面去思考,從問題的結果出發,一步一步退回到已知信息,從而找到解決問題的辦法。當我們解決問題時遇到了障礙,有困難的時候,可以換個角度思考,或許會出現柳暗花明又一村的美景。
如:下面的例題。題目是:4個小朋友共有課讀物100本。甲給乙3本,乙給丙4本,丙給丁5本,丁給甲6本,這時四個人課外讀物的本數相等。四個人原來各有多少本?這道題如果順著題意思考的話會感覺到很復雜,無從下手。但是如果倒過來想,反而很容易獲得解決辦法。根據“最后四人本數相等”,可以知道每人現在有100÷4=25本。把給別人的要回來,即用加法;別人給的退回去,即用減法。這樣甲原來有25+3—6= 22本,乙原來有25+4—3= 26本,丙原來有25+5—4= 26本,丁原來有25+6—5= 26本。
本文提出的教學策略體系是建立在前人的已有研究成果之上。前人的研究成果中有很多值得我們借鑒和繼承。實際教學情況是復雜多變的,而學生解決問題的策略也是復雜多樣的,為了能夠提高小學生的解決問題的綜合能力,對本文所提出的教學策略體系也不易孤立地運用,應該綜合使用前人己有的有效教學策略,使它們優勢互補、相得益彰。

