淺談數學問題教學中的“源頭活水”

李遠斌

【摘要】 本文結合教學實踐，從“數學基礎知識及形成過程、數學問題的分析及思維形成過程、數學基本思想和方法的形成過程、教材典型問題的探究過程”等過程經驗四個方面，談抓好初中數學中的“源頭”教學。從而拓展學生的解題思路，提高學生的解題能力，提高學生探索問題的能力，為學生的數學學習源源不斷地注入“活水”。

【關鍵詞】 數學思想方法 典型問題 源頭活水

【中圖分類號】 G633.6 【文獻標識碼】 A 【文章編號】 1992-7711（2016）06-014-01

“問渠哪得清如許，為有源頭活水來。”在數學教學中，筆者常常思考如何利用“源頭”出“活水”，提高學生的學習效率，提高學生的自主學習能力，形成“學為中心”的數學課堂。數學“源頭”，就是數學基礎知識及形成過程、數學問題的分析及思維形成過程、數學基本思想和方法的形成過程、教材典型問題的探究過程等過程經驗。引導學生利用自身的這些經驗，解決數學問題，“活水”才能源源不斷出來。

一、數學基本知識的形成過程，是學生解決問題的“源頭”

數學基本知識，是在學生學習的過程中形成的，這個過程形成的經驗對學生很重要。如果基本知識是學生解決基本問題必要的數學理由，那么知識的形成過程的經驗就是學生后續學習、借鑒的基石。因此，數學基本知識和知識的形成過程經驗，是學生解決問題的兩個“源頭”。

二、數學問題的分析與思維形成過程，是培養學生形成良好的分析問題和解決問題的習慣的“源頭”

著名美籍匈牙利數學家、教育家、數學解題方法論的開拓者喬治·波利亞，他十分重視解題在數學學習中的作用，并對解題方法進行了多年的研究和實踐，終于繪制出一張“解題表”，表中把解題過程分為四個階段。學生分析解決問題的良好習慣。（一）弄清題意：已知（條件）是什么？未知（結論）是什么？（二）擬定計劃：見過這道題或與之類似的題嗎？能聯想起有關的定理或公式嗎？再看看未知數，換一種方式來敘述這道題，回到定義看看，先解決一個特例試試，這個問題的一般式是什么？你能解決問題的一部分嗎？你用了全部條件嗎？（三）實行計劃：實現你的解題計劃并檢驗每一步驟，證明你的每一步都是正確的。（四）回顧：檢查結果并檢驗其正確性；換一個方法做這個題；嘗試把你的結果和方法用到其它問題上。我們在教學過程中，要滲透波利亞的“問題表”，培養學生思考問題的良好習慣，這是學生分析問題和解決問題的重要“源頭”。

三、教材典型問題的探究過程，是學生學習模仿與創新的“源頭”

近年來，中考題越來越重視學生的能力考查，雖然問題的設置難度和背景有所變化，但基本都是源于教材，將教材上某些典型問題加以改編，很多問題也只是方法的遷移。因此，關注教材典型問題的分析過程，由此及彼，歸納總結，推廣應用，引導學生進行類比學習，促進學生自主學習。

四、數學基本思想與方法的形成過程，是學生能舉一反三的“源頭”

初中重要的數學思想有數形結合思想、方程函數思想、整體思想、分類討論思想、轉化思想等，重要的方法有待定系數法、消元法、配方法、換元法、圖像法等。這些重要的數學思想方法在學生的學習過程中有很重要的作用。數學思想方法的學習不能一蹴而就，而是在教學過程不斷反復的滲透，培養學生的數學思想方法的應用意識，才能較好地掌握。

例如，數形結合思想的典型應用浙教版 九下 P29 例5 P31 設計題

實質：以形助數，以數解形

（1）將方程、不等式轉為函數，利用函數圖象解決方程不等式的問題；

（2）將函數問題轉化為方程、不等式的問題，利用方程、不等式的性質解決函數問題。

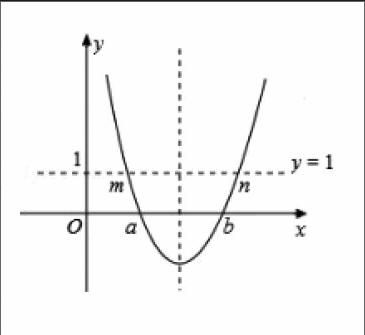
例. （2014·濟寧）“如果二次函數y=ax2+bx+c的圖象與x軸有兩個公共點，那么一元二次方程ax2+bx+c=0有兩個不相等的實數根。”請根據你對這句話的理解，解決下面問題：若m、n（m

A.m

C.a

分析：依題意，畫出函數y=（x﹣a）（x﹣b）的圖象，如圖所示。

函數圖象為拋物線，開口向上，與x軸兩個交點的橫坐標分別為a，b（a

方程1﹣（x﹣a）（x﹣b）=0轉化為（x﹣a）（x﹣b）=1，方程的兩根是拋物線y=（x﹣a）（x﹣b）與直線y=1的兩個交點。

由m

由拋物線開口向上，則在對稱軸左側，y隨x增大而減少，則有m

綜上所述，可知m

五、總結

布魯納曾說：“我們教一個科目，不是去建立一個有關該科目的小型圖書館，而是要學生自行思考，像一名數學家那樣去思考數學，像史學家那樣去探索歷史，投入到獲得知識的過程中去。”如果教師在教學時，多注意在源頭上下點功夫，能更多地把視點放在通過學生的領悟和教師的講評來達到知識的回顧、鞏固、再學習、再認識的動態過程而絕非僅僅是追求學習結果，在知識的形成、分析問題的習慣、典型問題的分析總結和數學思想方法的滲透在學習的過程中，讓學領悟學習的真諦，那么才能真正地把數學知識化解到學生的思維和能力中，進而達到培養學生能力，提高學生數學素質的目的，而只有如此教師才能為提升數學學習的效率注入源源不斷的活水。

參考文獻：