議“柯克曼女生問題”

【摘要】“柯克曼女生問題”實質就是解決STS（v）、KTS（v），LSTS（v）、LKTS（v）等組合設計的存在性、構造及其可解數.文章在“K題”、“J題”可解性的基礎上，列舉了六種類型“K題”和一種“J題”的人工構造方法，并從不同角度探討了可解總數的7種推算結果.

【關鍵詞】柯克曼女生問題；K題J題；充要條件；解法；解數

【中圖分類號】O157.1 【文獻標識碼】A

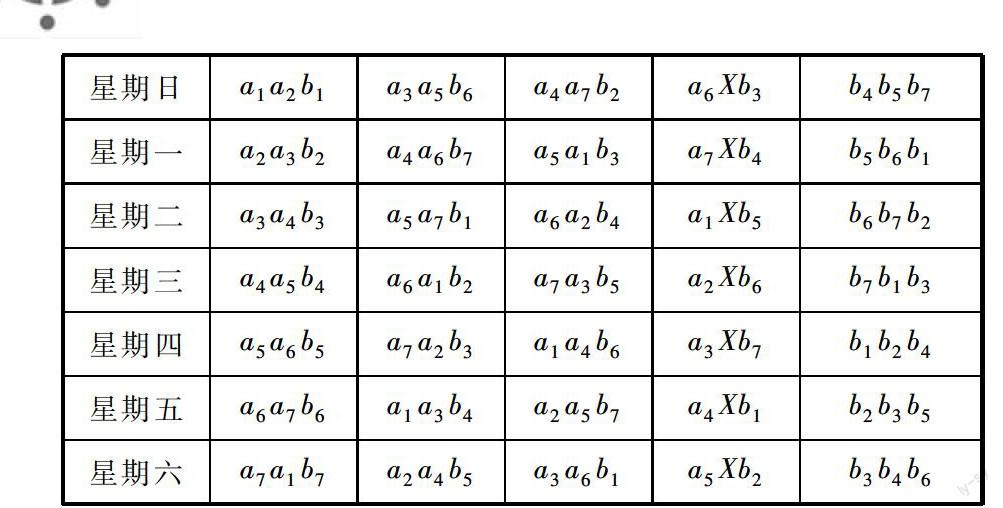
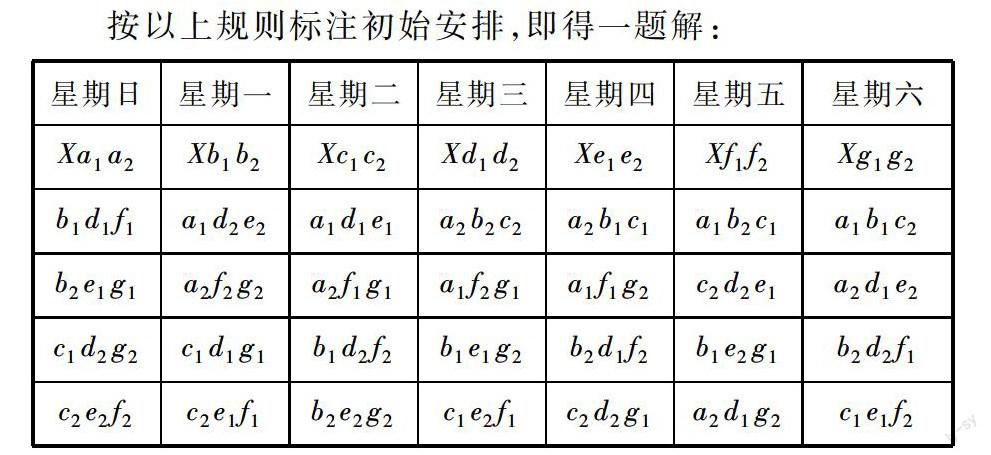
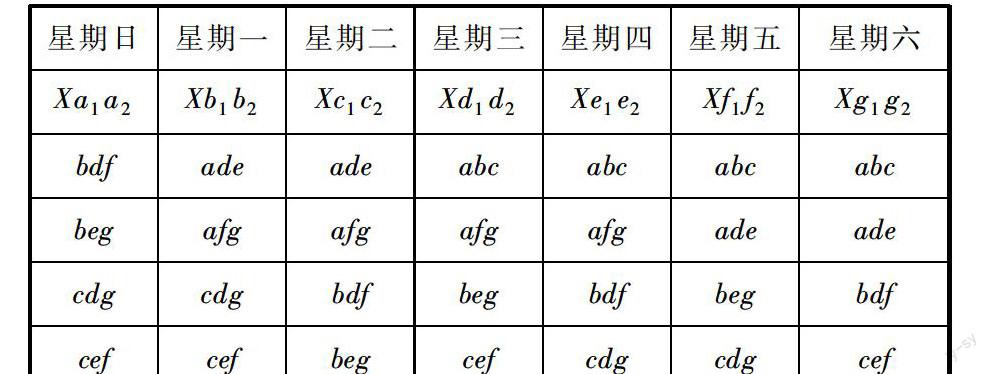
“柯克曼女生問題”，是因英國數學家柯克曼（T.P.Kirkman）1847年在《女士與先生之日記》雜志上，發表了一篇題為“疑問六”的女生散步命題而引出的.其意是：一位女教師帶領15名女學生散步，每3人一組共5組結伴而行.問能否安排一周7天的散步計劃，使其中任意2名女生曾被分到一組，且僅被分到一組？筆者將此命題簡稱為“K題”.之后英國數學家西爾菲斯特（J.J.Sylvester）和凱萊（A.Cayley），又于1850年將此題擴展為：能否安排13周的散步計劃，不但使每周都符合“K題”要求，而且使其中任意3名女生曾被分到一組，且僅被分到一組？筆者將此擴展題簡稱為“J題”.

“K題”“J題”先后提出后，從19世紀中葉開始，到20世紀，直至當今，從英國、德國、法國到美國，蘇聯（俄羅斯），到中國，無數學者和愛好者從組合數學理論對“K題”“J題”進行了百多年的研究、探討.他們絞盡腦汁、嘔心瀝血，前赴后繼地攻下了一道道難關，攀登了一個個險峰，創立出“組合設計”這一新理論，為組合數學增添了一個重要分支，推動著現代應用數學的發展！

把v元集X（v）中的元，按k個元一組的子集（稱作區組）共b個進行配置，這種組合設計的類型稱作區組設計.若使每個元在b 個區組中出現γ次……