數形結合談數軸
潘盛發(廣西欽州市欽北區長灘中學)
數形結合談數軸
潘盛發
(廣西欽州市欽北區長灘中學)
探索數形結合的思想在數學中的應用,培養學生的數形結合意識,加強數形結合思想的訓練,體現數形結合思想在教學中的基礎性和重要性。
數形結合;數軸;應用
數形結合的思想就是將數學中抽象的數學語言、數量關系與具體直觀的圖像結合起來,利用抽象的思維和形象思維的有機結合,借助形的具體明確來反映數量之間的關系,借助數來具體描述形的本質內涵,用這種數形結合的思想來解決數學中某些問題往往可以使復雜的問題簡單化,抽象的問題具體化,同時也便于對概念的理解和掌控。
在七年級的數學中,學習的數軸就是數形結合的最好例子。我們初次學習負數、相反數、絕對值以及有理數這些概念時,往往在理解上有一些困難,如果通過數軸來幫助理解,就可以解決這個問題。
數軸可以在以下幾個方面幫助我們理解有關數的概念和解題中的應用。
一、利用數軸形象地表示有理數
數軸是規定了原點、正方向和單位長度的直線,零用原點來表示,正數用原點右側的點表示,負數用原點左側的點表示,這樣就使較抽象的數能通過直觀、形象的數軸上的點表示出來。
例:在數軸上表示有理數+2,0,-3。
在數軸上用0表示原點,A點表示+2,也就是A點在原點右側,距原點有2個長度單位,用B點表示-3,也就是B點在原點左側,距原點有3個長度單位。(如圖1)

圖1
二、利用數軸比較直觀地理解相反數
只有符號不同的兩個數叫做互為相反數。如5與-5、2與-2都是互為相反數。如果把這一概念與直觀的數軸聯系起來,那么互為相反數的兩個數可以表示為數軸上的兩個點,這兩個點分別位于原點兩側,且它們到原點的距離相等。這樣,相反數概念在數軸上得到了直觀的解釋。
例:在數軸上表示+4和-4,并判斷它們是否互為相反數。
用A點表示+4,用B點表示-4,A點和B點在原點兩側,且到原點的距離都是4個長度單位,符合對于相反數的要求,因此+4和-4是互為相反數。(如圖2)

圖2
三、利用數軸比較有理數的大小
許多學生在比較兩個有理數大小時,對法則理解不透,因而常常出錯。若是把數軸利用起來,就會減少錯誤的出現。在比較有理數大小時,可以先在數軸上用點表示有理數,再觀察哪個點在右,哪個點在左,因為左邊的點表示的數比右邊的點表示的數小。那從左到右,數軸上的點表示的數是由小到大的,因此,就把比較數的大小問題,轉化成排列點的順序問題,學生就很容易掌握。
例:在數軸上表示下列各數,并用“<”連接起來。
+3,-2,-3,+1,0。
根據題目要求,在數軸上把對應點找出來,從而就把5個點的左右順序排定(如圖3),得到:
-3<-2<0<+1<+3。

圖3
四、利用數軸理解絕對值的意義
絕對值是中學數學中非常重要的概念,也是學習的難點之一,許多學生不能正確地理解這一概念,如果能借助數軸來理解這一概念,問題就會變得簡單、直觀。絕對值就是在數軸上表示這個數的點到原點的距離。因為兩點間的距離是非負的,因此,任何數的絕對值都是非負的,即|a|≥0(a是有理數)。
例如:+2的絕對值是2,-3的絕對值是3,0的絕對值是0,如圖4

圖4
在數軸上用C點表示+2,C點到原點的距離為2個長度單位,在數軸上用D點表示-3,D點到原點的距離為3個長度單位,因為原點到原點的距離為0,所以0的絕對值是0。
五、利用數軸求出不等式組的解集
一般的,幾個不等式和解集的公共部分,叫做由它們所組成的不等式的解集。先把每個不等式的解集在數軸上表示出來,從而利用數軸就可以直觀地確定不等式組的解集。
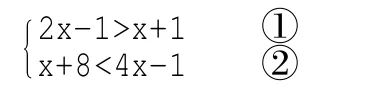
例:解下列不等式組
解:解不等式①得x>2
解不等式②2得x>3
把不等式①和②的解集在數軸上表示出來(如圖5)

圖5
從圖中可以找出兩個不等式解集的公共部分,得到不等式組的解集:x>3
數軸在其他方面還有更為廣泛的應用,隨著數的范圍的第二次擴充,還可以用數軸上的點表示全體實數等。
由于數形結合思想是一種深層的數學知識,它隱含于數學教材之中,教學的首要任務就在于引導充分發掘教材中的數形結合思想,而挖掘過程采用的主要方法是歸納和提煉。教師在教學過程中根據數學知識編排課程內容時,要注意根據學生的認識規律,滲透一些數形結合的初步思想。根據教學實際情況引導說明,抓住數形結合的思想引導學生學習,既借助代數方法研究圖形特征,這樣既有利于數形結合思想的闡述,又比較符合學生的心理發展規律和認識規律,有利于提高學生學習數學的興趣,開拓學生的解題思路,活躍課堂氣氛,發展學生的形象思維能力、空間想象能力等。
當學生弄清了數形結合思想以后,教師在數學基礎知識教學及解題指導中,應盡量體現數形結合思想的方法和運用,使其達到自覺、自由的熟練運用。
因此,在教學中教師要注意及時總結數形結合思想的特點,滲透數形結合意識,強化對數形結合思想的理解,要求學生在學習中能夠充分發揮數軸的直觀作用,使數形有機地結合,會使抽象的數學知識變得更形象,更直觀,更生動,提高學生學習數學的興趣,增強分析、解決問題的能力。
·編輯魯翠紅

