海上浮式風(fēng)電機(jī)半潛式平臺二階水動力計(jì)算與響應(yīng)特性分析

彭春江　胡燕平　程軍圣　沈意平

1.湖南大學(xué)汽車車身先進(jìn)設(shè)計(jì)制造國家重點(diǎn)實(shí)驗(yàn)室，長沙，4100822.湖南科技大學(xué)，湘潭，411201

?

海上浮式風(fēng)電機(jī)半潛式平臺二階水動力計(jì)算與響應(yīng)特性分析

彭春江1,2胡燕平2程軍圣1沈意平2

1.湖南大學(xué)汽車車身先進(jìn)設(shè)計(jì)制造國家重點(diǎn)實(shí)驗(yàn)室，長沙，4100822.湖南科技大學(xué)，湘潭，411201

提出了基于二次脈沖響應(yīng)函數(shù)法的海上浮式風(fēng)電機(jī)浮式平臺二階水動力計(jì)算方法，該方法基于三維勢流理論用直接積分法求浮式平臺的二次傳遞函數(shù)，并結(jié)合波高時(shí)程，將二次脈沖響應(yīng)函數(shù)法應(yīng)用于浮式平臺二階水動力的計(jì)算。把計(jì)算所得二階水動力施加到海上浮式風(fēng)電機(jī)整機(jī)時(shí)域動力學(xué)計(jì)算模型，計(jì)算二階水動力的激勵響應(yīng)。以DeepCwind半潛式平臺為算例，其上支撐美國可再生能源實(shí)驗(yàn)室5MW參考風(fēng)機(jī)。先對所提出的二階水動力計(jì)算方法進(jìn)行驗(yàn)證，再分別在無風(fēng)和有風(fēng)條件下，計(jì)算一階水動力單獨(dú)激勵響應(yīng)和一階二階水動力共同激勵響應(yīng)，通過對比響應(yīng)幅值譜、響應(yīng)統(tǒng)計(jì)值，分析二階水動力的激勵特性。結(jié)果表明,對于半潛式平臺，慢漂力和平均漂移力有明顯的激勵作用，和頻二階水動力的激勵作用可以忽略。

海上浮式風(fēng)電機(jī)；半潛式平臺；二階水動力；二次傳遞函數(shù)；響應(yīng)特性

0　引言

為了開發(fā)水深超過60 m海域的風(fēng)資源，在海上風(fēng)電機(jī)組中配置固定式基座不再經(jīng)濟(jì)可行，因此提出了用浮式平臺支撐風(fēng)電機(jī)。浮式平臺由于受到波的激勵作用，其水動力特性相比固定式基座復(fù)雜得多，這使得浮式風(fēng)電機(jī)整機(jī)動力學(xué)特性更加復(fù)雜。因此浮式平臺水動力特性是海上風(fēng)電技術(shù)研究的一個(gè)重要方面，而建立浮式平臺水動力計(jì)算模型是浮式平臺水動力研究的重要內(nèi)容之一，是研究浮式風(fēng)電機(jī)整機(jī)動力學(xué)特性的基礎(chǔ)。

二階水動力包括差頻及和頻二階水動力，差頻二階水動力又包括平均漂移力和慢漂力。對于傳統(tǒng)海上浮式結(jié)構(gòu)，二階水動力相比一階水動力小一個(gè)數(shù)量級以上，對于海上浮式風(fēng)電機(jī)，二階水動力相比氣動力更小，且存在氣動阻尼，因此，目前對海上浮式風(fēng)電機(jī)浮式平臺水動力計(jì)算，只考慮一階水動力，忽略了二階及以上的水動力[1]。但Goupee等[2]和Koo等[3]在風(fēng)、浪水池中，對海上浮式風(fēng)電機(jī)進(jìn)行模型測試，發(fā)現(xiàn)二階水動力相比一階水動力和氣動力雖然很小，但在不同的風(fēng)浪環(huán)境下，能激起浮式平臺的特征模態(tài)，產(chǎn)生共振響應(yīng)，影響海上浮式風(fēng)電機(jī)的運(yùn)行性能和系泊系統(tǒng)的疲勞壽命。因此，在海上浮式風(fēng)電機(jī)浮式平臺水動力計(jì)算中考慮二階水動力是必要的。

López-Pavón等[4]、Coulling等[5]根據(jù)二次傳遞函數(shù)和波高時(shí)程，用紐曼近似法計(jì)算浮式平臺的二階水動力。紐曼近似法計(jì)算簡單，有計(jì)算時(shí)間短的優(yōu)勢，但只有當(dāng)浮體的固有頻率很低且處在深水海域時(shí)計(jì)算出的二階水動力才是有效的，而用二次脈沖響應(yīng)函數(shù)法求平臺的二階水動力是一種相對直接的方法，雖然計(jì)算時(shí)間比紐曼近似法要長，但計(jì)算結(jié)果更接近試驗(yàn)測試數(shù)據(jù)[6]，且沒有應(yīng)用范圍的約束，更具通用性。

Karimirad[7]利用傳統(tǒng)海上結(jié)構(gòu)物時(shí)域非線性動力學(xué)計(jì)算程序計(jì)算風(fēng)電機(jī)浮式平臺的二階水動力響應(yīng)，計(jì)算中把風(fēng)輪簡化為風(fēng)盤進(jìn)行簡單的風(fēng)力計(jì)算，這樣得到的二階水動力響應(yīng)與實(shí)際情況相差較大。Roalda等[1]、Bayati等[8]在頻域根據(jù)二次傳遞函數(shù)直接求海上浮式風(fēng)電機(jī)浮式平臺二階水動力響應(yīng)，由于頻域計(jì)算不能考慮瞬態(tài)響應(yīng)過程，只能得到二階水動力的穩(wěn)態(tài)響應(yīng)。而基于海上浮式風(fēng)電機(jī)整機(jī)動力學(xué)計(jì)算模型，在時(shí)域計(jì)算浮式平臺二階水動力響應(yīng)更符合實(shí)際情況。

因此，本文基于三維勢流理論用直接積分法求浮式平臺的二次傳遞函數(shù)，結(jié)合波高時(shí)程，將二次脈沖響應(yīng)函數(shù)法應(yīng)用于海上浮式風(fēng)電機(jī)浮式平臺二階水動力計(jì)算，在海上浮式風(fēng)電機(jī)整機(jī)時(shí)域動力學(xué)計(jì)算模型的基礎(chǔ)上，計(jì)算浮式平臺在各種環(huán)境激勵下的響應(yīng)，通過對比響應(yīng)幅值譜、響應(yīng)統(tǒng)計(jì)值，分析二階水動力的激勵特性。

1　二階水動力計(jì)算

描述浮式風(fēng)電機(jī)浮式平臺的運(yùn)動及載荷需定義兩個(gè)坐標(biāo)系：①慣性參考坐標(biāo)系OXYZ,其中X軸為順風(fēng)向，Z軸沿風(fēng)電機(jī)塔架軸線垂直向上，原點(diǎn)O為Z軸與平均海平面(MSL)的交點(diǎn)，Y軸方向由右手定則確定；②平臺隨體坐標(biāo)系O′X′Y′Z′，在未擾動位置時(shí)與OXYZ重合，該坐標(biāo)系隨平臺的移動改變原點(diǎn)位置，隨平臺的轉(zhuǎn)動改變方向。原點(diǎn)O′在慣性參考坐標(biāo)系OXYZ中的三個(gè)坐標(biāo)分量即為風(fēng)電機(jī)浮式平臺的三個(gè)平移量，X′相對X軸、Y′相對Y軸、Z′相對Z軸的轉(zhuǎn)動量即為平臺的三個(gè)轉(zhuǎn)動量，原點(diǎn)O′為浮式平臺的計(jì)算參考點(diǎn)。定義與X方向一致的波向和風(fēng)向?yàn)?°波向和風(fēng)向。圖1為坐標(biāo)系的示意圖。

圖1　參考坐標(biāo)系

本文水動力計(jì)算理論中的幾個(gè)假設(shè)：①入射波的幅值比波長小得多，這就允許使用簡單的入射波運(yùn)動學(xué)理論，如線性波理論；②相比浮式平臺的大小(也即平臺的特征長度)，浮式平臺的運(yùn)動量很小，這樣，利用勢流理論，在平臺未擾動位置計(jì)算得到的水動力可以施加在擾動后平臺的計(jì)算參考點(diǎn)；③浮式平臺是剛性的；④平穩(wěn)海況下波面高度是呈高斯分布的隨機(jī)過程，且是線性的。

1.1不規(guī)則波波高時(shí)程計(jì)算

在不規(guī)則海況，根據(jù)假設(shè)①和④，波高時(shí)程可以用高斯白噪聲過程經(jīng)過線性濾波得到。本文所用實(shí)現(xiàn)方法是，在頻域用Box-Muller法計(jì)算高斯白噪聲過程，在給定海浪譜的前提下，根據(jù)平穩(wěn)線性系統(tǒng)輸入輸出功率譜關(guān)系求得波高的頻域表示，通過傅里葉反變換求得波高時(shí)程。

在浮式平臺參考點(diǎn)處，不規(guī)則波的波高可表示為有隨機(jī)相位的規(guī)則波之和：

(1)

式中，ζi為單個(gè)規(guī)則波的波幅；ωi為波頻率；εi為相位。

在本文中ζ(0,0,0,t)簡寫為ζ(t)，ζ(t)用高斯白噪聲過程經(jīng)過線性濾波得到：

(2)

式中，w(τ)為均值為0、標(biāo)準(zhǔn)差為1的高斯白噪聲隨機(jī)變量；h(t)為線性濾波傳遞函數(shù)。

在頻域根據(jù)平穩(wěn)線性系統(tǒng)輸入輸出功率譜關(guān)系，經(jīng)傅里葉反變換可求得波高ζ(t)為

(3)

式中，S2-Sided(ω)為波高的雙側(cè)功率譜；W(ω)為w(τ)的傅里葉變換。

W(ω)用Box-Muller法計(jì)算得到：

1.2二階水動力計(jì)算

二階水動力的計(jì)算方法是先基于三維勢流理論，用直接積分法求出海上浮式風(fēng)電機(jī)浮式平臺的二次傳遞函數(shù)，再對二次傳遞函數(shù)進(jìn)行雙重傅里葉反變換求得二次脈沖響應(yīng)函數(shù)，最后在時(shí)域，利用二次脈沖響應(yīng)函數(shù)與波高的雙重卷積求總的二階水動力。實(shí)現(xiàn)方法是在頻域中根據(jù)波高和二次傳遞函數(shù)求出二階水動力，再進(jìn)行傅里葉反變換求時(shí)域二階水動力。

利用勢流理論，對浮體濕表面進(jìn)行直接壓力積分獲得二階水動力的通用表達(dá)式為

(4)

其中，變量中的上標(biāo)(1)、(2)分別表示一階量、二階量，為哈密頓算符，M為浮體的質(zhì)量矩陣，q為浮體平移位移矩陣，為浮體平移加速度矩陣，Ω為浮體角位移矩陣，WL表示水線，S表示濕表面，n為濕表面面元的外法線向量，(1)φ、(2)φ為速度勢，ζrel為相對水線的波高。式(4)的前三項(xiàng)都是一階解的二次作用，根據(jù)一階解可全部確定，最后一項(xiàng)與二階速度勢有關(guān)，可用勢流理論確定。式(4)的表達(dá)不方便計(jì)算，因此基于式(1)的波高表示，經(jīng)推導(dǎo)，總二階水動力可表示成如下形式：

(5)

根據(jù)二次傳遞函數(shù)求二次脈沖響應(yīng)函數(shù)gi(t1,t2)：

在時(shí)域用二次脈沖響應(yīng)函數(shù)計(jì)算總二階水動力為

(6)

2　數(shù)值計(jì)算

本文根據(jù)式(6)用數(shù)值計(jì)算方法實(shí)現(xiàn)對和頻、差頻二階水動力的求解。首先對時(shí)間和頻率進(jìn)行離散，在頻域根據(jù)波高和二次傳遞函數(shù)計(jì)算每一離散頻率點(diǎn)的二階水動力，再用離散傅里葉逆變換求得離散時(shí)間點(diǎn)上的二階水動力，然后通過插值法求任意時(shí)刻的二階水動力。

(7)

其中，m取小于N/4的全部正整數(shù)，其余頻率點(diǎn)補(bǔ)零。第二項(xiàng)和頻二階水動力頻域離散值：

(8)

其中，k取小于m/2的全部正整數(shù)。

通過離散傅里葉逆變換求得時(shí)域離散值分別為

(9)

(10)

其中，IDFT{}表示離散傅里葉逆變換。和頻二階水動力時(shí)域離散值為

(11)

圖2　和頻二階水動力計(jì)算流程

(12)

差頻二階水動力的非零頻分量也稱慢漂力，其頻域離散值為

(13)

其中，k取小于N/2-m的所有正整數(shù)。

慢漂力的時(shí)域離散值為

(14)

(15)

差頻二階水動力的計(jì)算流程與和頻二階水動力的相似，這里就不再給出。

3　算例與分析

3.1計(jì)算對象與參數(shù)

基于以上二階水動力計(jì)算理論，結(jié)合浮式風(fēng)電機(jī)整機(jī)時(shí)域動力學(xué)計(jì)算模型，針對支撐美國可再生能源實(shí)驗(yàn)室(NREL)5MW參考風(fēng)機(jī)[9]的DeepCwind半潛式平臺[10]進(jìn)行各種響應(yīng)計(jì)算，浮式平臺外形如圖3所示，結(jié)構(gòu)尺寸如表1所示，質(zhì)量屬性參數(shù)如表2所示，6個(gè)自由度的固有頻率如表3所示，風(fēng)機(jī)的性能尺寸詳見文獻(xiàn)[9]。本文計(jì)算方法同樣可應(yīng)用于風(fēng)電機(jī)其他浮式平臺。

圖3　DeepCwind半潛式平臺及風(fēng)電機(jī)示意圖

表1　半潛式平臺結(jié)構(gòu)尺寸　m

表2　半潛式平臺質(zhì)量參數(shù)

表3　半潛式平臺6個(gè)自由度的固有頻率

浮式平臺水動力計(jì)算選用單向不規(guī)則波模型，采用JONSWAP波譜，波向與平臺縱蕩方向一致，表4所示為本文計(jì)算選用的3種波況。有效波高Hs的值4.5 m、7.1 m、11.8 m分別代表中等、嚴(yán)峻、極限三種海況。圖4所示為所用3種有效波高的波譜S(ω)，圖5所示為Hs=7.1 m時(shí)平臺參考點(diǎn)處的波高時(shí)程ζ(t)。從波譜圖可知，有效波高不同，一階波頻區(qū)間稍有不同，為了減少二階水動力計(jì)算量，根據(jù)一階波頻區(qū)間確定差頻、和頻二階水動力的計(jì)算范圍如表5所示。由表3可知，半潛式平臺6個(gè)自由度的固有頻率都處于中等海況一階波頻區(qū)間之外的低頻段。對于嚴(yán)峻和極限海況，垂蕩固有頻率處于一階波譜區(qū)間。

表4　計(jì)算波況(JONSWAP譜)

圖4　有效波高分別為4.5 m、7.1 m、11.8 m的JONSWAP譜

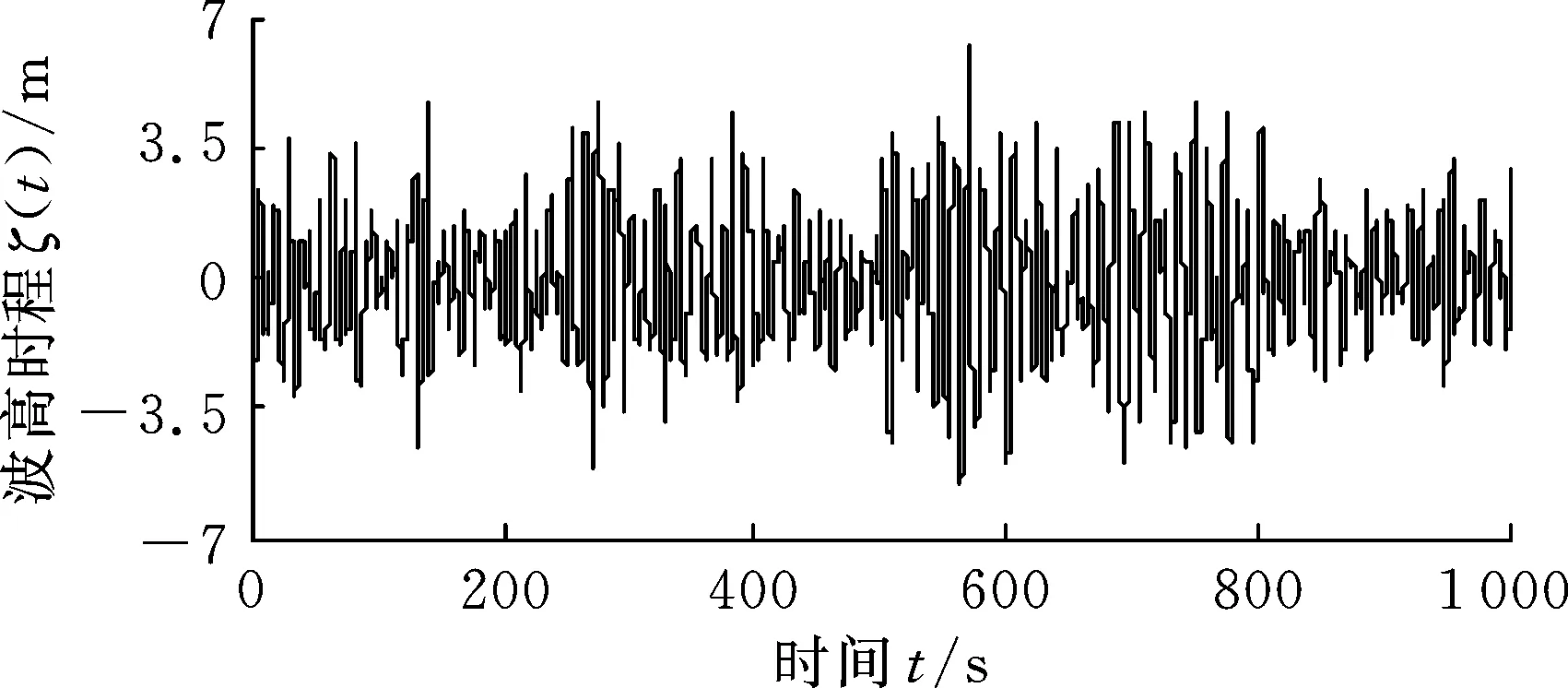
圖5　有效波高為7.1 m時(shí)參考點(diǎn)處的波高時(shí)程

表5　二階水動力計(jì)算頻率范圍　Hz

為了深入理解波頻作用，排除湍流風(fēng)低頻激勵作用的影響，選用穩(wěn)態(tài)風(fēng)進(jìn)行激勵，計(jì)算風(fēng)速8 m/s、16 m/s、23 m/s分別代表風(fēng)機(jī)額定風(fēng)速以下、額定風(fēng)速以上、臨近切出風(fēng)速時(shí)的風(fēng)況。風(fēng)向與波向一致，也即0°風(fēng)向。

浮式風(fēng)電機(jī)整機(jī)動力學(xué)計(jì)算的氣動載荷模型采用葉素動量定理，考慮輪轂、葉尖損失。結(jié)構(gòu)動力學(xué)建模采用凱恩方法結(jié)合模態(tài)疊加法，系泊系統(tǒng)采用準(zhǔn)靜態(tài)模型，一階水動力計(jì)算模型參考文獻(xiàn)[9]，拖曳阻力采用莫里森公式中的拖曳項(xiàng)計(jì)算。水深200 m，平臺吃水20 m，平臺構(gòu)件所用拖曳系數(shù)：主圓柱0.58，上圓柱0.61，基圓柱0.68，支架0.63。本算例中所使用的附加縱蕩線性阻尼為1×106N/(m/s)，附加橫搖和縱搖線性剛度為1.45×109N·m/rad，附加縱蕩二次阻尼為2.25×106N/(m/s)2，附加二次縱搖阻尼為5×106N·m/(rad/s)2。浮式平臺響應(yīng)計(jì)算時(shí)長為1000 s，取后500 s進(jìn)行統(tǒng)計(jì)值計(jì)算。

3.2二階水動力計(jì)算方法驗(yàn)證

文獻(xiàn)[2-3]對本算例中的半潛式浮式風(fēng)電機(jī)進(jìn)行了1∶50比例模型風(fēng)浪水池測試。圖6所示為在無風(fēng)波況2作用下，半潛式平臺縱蕩和縱搖響應(yīng)功率譜Pi(ω) 的計(jì)算結(jié)果與試驗(yàn)結(jié)果。從圖6可以看出計(jì)算結(jié)果與試驗(yàn)結(jié)果基本一致，這說明水動力(包括一階和二階)計(jì)算模型和方法是可行的。在低頻段，縱蕩和縱搖固有頻率處的共振峰由差頻二階力激勵所致，用本文二階水動力計(jì)算方法很好地呈現(xiàn)了試驗(yàn)結(jié)果，這說明本文二階水動力計(jì)算方法的正確性。

(a)縱蕩響應(yīng)功率譜

(b)縱搖響應(yīng)功率譜圖6　無風(fēng)波況2作用下，一階二階水動力共同激勵響應(yīng)功率譜計(jì)算結(jié)果與測試結(jié)果

3.3響應(yīng)計(jì)算與分析

本文針對以下兩種激勵條件，計(jì)算和分析二階水動力對半潛式平臺的激勵響應(yīng)：①無風(fēng)只有波激勵；②風(fēng)、浪聯(lián)合激勵。對應(yīng)海上浮式風(fēng)電機(jī)的正常運(yùn)行狀態(tài)和生存狀態(tài)，處于正常運(yùn)行狀態(tài)時(shí)受風(fēng)、浪的聯(lián)合激勵，處于生存狀態(tài)時(shí)風(fēng)電機(jī)停機(jī)，風(fēng)輪葉片順槳，此時(shí)風(fēng)大但風(fēng)力小，主要受波力的作用，與無風(fēng)只有波激勵的情況相似。

3.3.1無風(fēng)二階水動力激勵特性

圖7所示為無風(fēng)、波高為7.1 m時(shí)，一階水動力單獨(dú)激勵與一階二階水動力共同激勵下，平臺各自由度的響應(yīng)幅值譜Ai(ω)。從圖7可知，在無風(fēng)條件下，0°波向的二階水動力在橫搖固有頻率處激起了明顯的共振峰，但激勵幅值很小，可視為無響應(yīng)，考慮二階水動力對橫搖的影響無實(shí)際意義。橫蕩和艏搖也是如此，幅值譜就不再給出。對于縱蕩和縱搖，一階水動力在整個(gè)低頻區(qū)間0～0.056 Hz有一定的激勵幅值，在固有頻率處甚至有幅值不大的一階水動力共振峰。二階水動力對整個(gè)低頻區(qū)間的激勵有所增強(qiáng)，在固有頻率處激起了大幅值的共振峰。垂蕩固有頻率為0.058 Hz，處于一階波頻區(qū)間，從垂蕩幅值譜可見一階水動力在固有頻率附近激勵幅值較大。二階水動力在整個(gè)低頻區(qū)間對垂蕩的激勵都較弱。在波高為4.5 m和11.8 m的海況中，半潛式平臺各自由度的響應(yīng)幅值譜與波高為7.1 m海況的響應(yīng)幅值譜相似，因此其他兩種海況下的響應(yīng)幅值譜不再給出。

(a)縱蕩響應(yīng)幅值譜

(b)垂蕩響應(yīng)幅值譜

(c)橫搖響應(yīng)幅值譜

(d)縱搖響應(yīng)幅值譜圖7　波高7.1 m、無風(fēng)時(shí)，一階水動力激勵和一階二階水動力共同激勵響應(yīng)幅值譜

表6所示為無風(fēng)條件下，波高分別為4.5 m、7.1 m、11.8 m時(shí)，一階水動力單獨(dú)激勵和一階二階水動力共同激勵平臺各自由度響應(yīng)均值和標(biāo)準(zhǔn)差。從表6可看出，一階二階水動力共同激勵與一階水動力單獨(dú)激勵響應(yīng)之間存在均值差和標(biāo)準(zhǔn)差差值。均值差主要是平均漂移力激勵所致，因此可用均值差衡量平均漂移力的激勵作用。標(biāo)準(zhǔn)差可衡量響應(yīng)的振蕩幅值，用標(biāo)準(zhǔn)差差值衡量慢漂力的激勵作用。

表6　無風(fēng)不同波高條件下，平臺一階波激勵與一階二階波共同激勵響應(yīng)統(tǒng)計(jì)值

表7所示為無風(fēng)條件下，波高分別為4.5 m、7.1 m、11.8 m時(shí)，一階水動力單獨(dú)激勵和一階二階水動力共同激勵平臺各自由度響應(yīng)均值差和標(biāo)準(zhǔn)差差值。從表7可知，在三種海況下，平均漂移力會使縱蕩響應(yīng)發(fā)生較大的漂移，垂蕩和縱搖響應(yīng)的漂移值較小。各自由度響應(yīng)均值差隨波高變化，但不是單調(diào)的。縱蕩響應(yīng)標(biāo)準(zhǔn)差差值最大，縱搖次之，垂蕩很小，這說明慢漂力對縱蕩和縱搖可以激起較大的振蕩幅值，對垂蕩的激勵作用很弱。標(biāo)準(zhǔn)差差值隨波高變化，也不是單調(diào)的，因此平均漂移力和慢漂力對平臺各自由度的激勵作用會隨波高變化，但不是單調(diào)的。

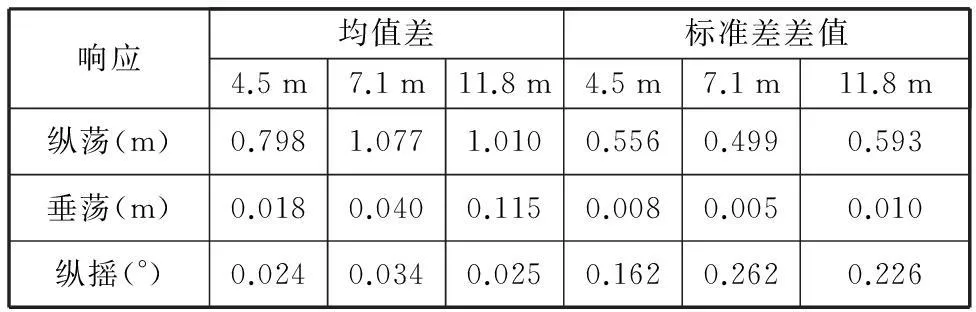
表7　無風(fēng)不同波高情況下，平臺一階波激勵與一階二階波共同激勵響應(yīng)均值差和標(biāo)準(zhǔn)差差值

3.3.2風(fēng)浪聯(lián)合作用下二階水動力激勵特性

圖8所示為波高7.1 m、風(fēng)速8 m/s時(shí)，一階水動力單獨(dú)激勵和一階二階水動力共同激勵下，平臺各自由度響應(yīng)幅值譜。從圖8看到，在風(fēng)浪聯(lián)合作用下，一階水動力在橫搖固有頻率附近激起了明顯的共振峰，二階水動力增強(qiáng)了共振峰，但幅值很小，橫蕩和艏搖的情況也是如此，相似的圖就不再給出。

圖8中，對于縱蕩和縱搖，一階水動力在整個(gè)低頻段有一定的激勵幅值，二階水動力在固有頻率附近出現(xiàn)了幅值不大的共振峰。對于垂蕩，一階水動力在0.058 Hz附近的激勵幅值較大，這是固有頻率處于一階波頻區(qū)間的緣故，二階水動力在整個(gè)低頻范圍稍有增強(qiáng)激勵幅值。對波高為7.1 m，風(fēng)速分別為16 m/s、23 m/s，波高為4.5 m和11.8 m，風(fēng)速分別為8 m/s、16 m/s、23 m/s的風(fēng)浪聯(lián)合激勵響應(yīng)幅值譜與圖8相似，因此不再給出圖。

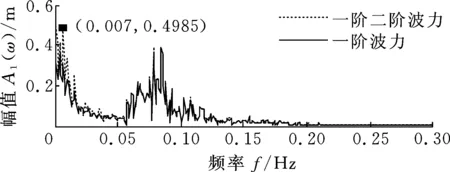
(a)縱蕩響應(yīng)幅值譜

(b)垂蕩響應(yīng)幅值譜

(c)橫搖響應(yīng)幅值譜

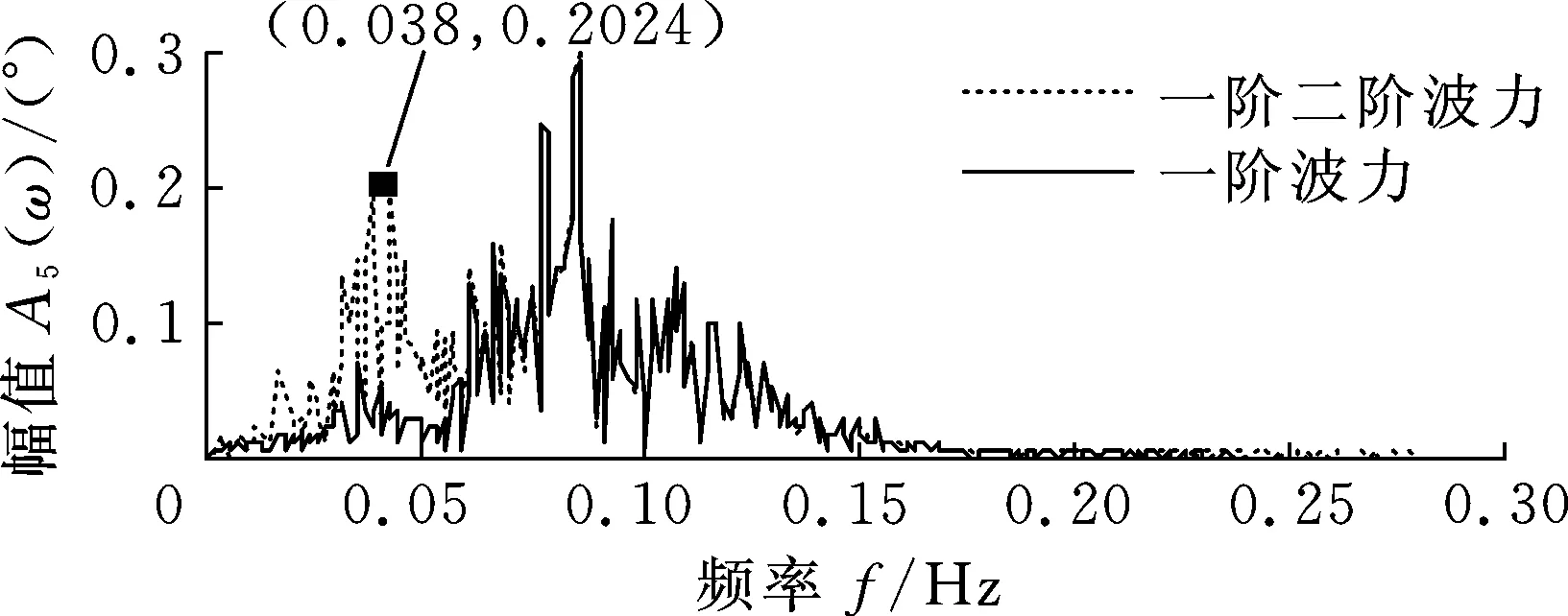
(d)縱搖響應(yīng)幅值譜圖8　波高7.1 m、風(fēng)速8 m/s時(shí)，一階水動力激勵和一階二階水動力共同激勵響應(yīng)幅值譜

表8是波高為7.1 m，風(fēng)速分別為8 m/s、16 m/s、23 m/s時(shí)，一階水動力單獨(dú)激勵和一階二階水動力共同激勵響應(yīng)統(tǒng)計(jì)值。從表8可知，縱蕩均值差在不同風(fēng)速下約為1 m，隨風(fēng)速變化很小，垂蕩和縱搖響應(yīng)均值差不大，隨風(fēng)速基本不變。這說明平均漂移力對縱蕩響應(yīng)的影響較大，對垂蕩和縱搖響應(yīng)的影響較小，且基本上不受風(fēng)速的影響。縱搖標(biāo)準(zhǔn)差在三種風(fēng)速下分別為0.125、0.140、0.160，縱蕩和垂蕩的標(biāo)準(zhǔn)差差值比縱搖小一個(gè)數(shù)量級，且各自由度的標(biāo)準(zhǔn)差差值隨風(fēng)速變化很小。這說明在風(fēng)浪聯(lián)合作用下，慢漂力對半潛式平臺各自由度的激勵作用都較弱，且隨風(fēng)速變化基本不變。

表9是風(fēng)速為8 m/s，波高分別為4.5 m、7.1 m、11.8 m時(shí)，一階水動力單獨(dú)激勵和一階二階水動力共同激勵響應(yīng)統(tǒng)計(jì)值。從表9可知，縱蕩、垂蕩、縱搖均值差隨波高變大，標(biāo)準(zhǔn)差差值總體來說都很小，隨波高有變化，但不是單調(diào)的。這說明在風(fēng)浪聯(lián)合作用下，平均漂移力對縱蕩、垂蕩、縱搖的激勵作用隨波高變化，即波高越大，激勵作用越強(qiáng)。

表8　波高7.1 m時(shí)，不同風(fēng)速下一階水動力激勵和一階二階水動力共同激勵響應(yīng)均值差和標(biāo)準(zhǔn)差差值

表9　風(fēng)速8 m/s時(shí)，不同波高下一階水動力激勵和一階二階水動力共同激勵響應(yīng)均值差和標(biāo)準(zhǔn)差差值

慢漂力對半潛式平臺各自由度的激勵作用都較弱，且隨波高有相對較大的變化。

3.3.3其他激勵特性對比

圖9是波高4.5 m，無風(fēng)和有風(fēng)一階二階水動力共同激勵下，半潛式平臺縱蕩和縱搖響應(yīng)幅值譜，有風(fēng)時(shí)的風(fēng)速為8 m/s。從圖9可知，對于縱蕩和縱搖，有風(fēng)條件下二階水動力激勵幅值相比無風(fēng)時(shí)的要小很多，這是因?yàn)樵谟酗L(fēng)條件下存在氣動阻尼，抑制了二階水動力的激勵作用。

(a)縱蕩響應(yīng)幅值譜

(b)縱搖響應(yīng)幅值譜圖9　波高4.5 m，風(fēng)速8 m/s，無風(fēng)和有風(fēng)一階二階波共同激勵浮式平臺自由度響應(yīng)幅值譜

在有風(fēng)條件下，本文計(jì)算的縱蕩和縱搖響應(yīng)幅值譜與文獻(xiàn)[2]試驗(yàn)測得的響應(yīng)譜有差別，文獻(xiàn)[2]中氣動阻尼幾乎完全抑制了低頻共振響應(yīng)，而本文在低頻段仍有較小的響應(yīng)幅值，這是由于在計(jì)算模型中縱蕩和縱搖阻尼過小造成的。

從圖7、圖8還可看出，在和頻二階水動力計(jì)算頻率范圍0.112～0.480 Hz，縱蕩、垂蕩及縱搖響應(yīng)幅值譜幾乎不受二階水動力的影響，這說明在無風(fēng)或有風(fēng)條件下，和頻二階水動力對半潛式平臺的激勵作用可以忽略。

4　結(jié)論

本文針對海上浮式風(fēng)電機(jī)，提出浮式平臺二階水動力的通用計(jì)算方法，并結(jié)合海上浮式風(fēng)電機(jī)整機(jī)時(shí)域動力學(xué)計(jì)算模型。以支撐美國可再生能源實(shí)驗(yàn)室(NREL)5MW參考風(fēng)機(jī)的DeepCwind半潛式平臺為算例，在無風(fēng)或有穩(wěn)態(tài)風(fēng)時(shí)，在一階二階水動力共同激勵下，用本文計(jì)算方法計(jì)算的縱蕩、縱搖響應(yīng)譜與文獻(xiàn)[2]試驗(yàn)測得的響應(yīng)譜相近，驗(yàn)證了本文計(jì)算方法的可行性。

基于本文提出的計(jì)算方法，通過對算例的計(jì)算和分析，結(jié)果表明，對于半潛式浮式平臺在本文計(jì)算條件下有如下結(jié)論：

(1)在無風(fēng)或有風(fēng)時(shí)，可忽略和頻二階水動力的激勵作用，只考慮平均漂移力和慢漂力的激勵作用。

(2)在無風(fēng)時(shí)，慢漂力能激起縱蕩和縱搖特征模態(tài)，產(chǎn)生低頻共振響應(yīng)，且響應(yīng)幅值隨波高變化。平均漂移力對縱蕩的影響較大，對縱搖的影響較小，且隨波高變化。

(3)在風(fēng)浪聯(lián)合激勵下，由于存在氣動阻尼，慢漂力在縱蕩、縱搖固有頻率附近的激勵幅值明顯受到了抑制，隨風(fēng)速基本不變，隨波高有相對較大的變化。平均漂移力對縱蕩的激勵較強(qiáng)，對縱搖的激勵較弱，隨風(fēng)速基本不變，隨波高激勵增強(qiáng)。

(4)在無風(fēng)或有風(fēng)時(shí)，二階水動力對垂蕩的激勵作用都很弱。

[1]Roald L，Jonkman J，Robertson A，et al. The Effect of Second-order Hydrodynamics on Floating Offshore Wind Turbines[J]. Energy Procedia，2013,35:253-264.

[2]Goupee A J，Koo B，Kimball R W，et al. Experimental Comparison of Three Floating Wind Turbine Concepts[J]. Journal of Offshore Mechanics and Arctic Engineering, 2014,136(2):020906.

[3]Koo B，Goupee A J，Lambrakos K，et al. Model Tests for a Floating Windturbine on Three Different Floaters[J]. Journal of Offshore Mechanics and Arctic Engineering, 2014,136(2): 020907.

[4]López-Pavón C，Watai R A，Ruggeri F，et al. Influence of Wave Induced Second-order Forces in Semi-submersible FOWT Mooring Design[J].Journal of Offshore Mechanics and Arctic Engineering,2015,137(3):031602.

[5]Coulling A J，Goupee A J，Robertson A N，et al. Validation of a FAST Semi-submersible Floating Wind Turbine Numerical Model with DeepCwind Test Data[J]. Journal of Renewable and Sustainable Energy，2013,5(2):023116.

[6]Pinkster J A，Huijsmans R H M. The Low Frequency Motions of a Semi-submersible in Waves[C]//BOSS Conference.Cambridge,Massachusetts，1982:447-466.

[7]Karimirad M. Modeling Aspects of a Floating Wind Turbine for Coupled Wave-wind-induced Dynamic Analyses[J].Renewable Energy，2013,53:299-305.

[8]Bayati I，Jonkman J，Robertson A，et al. The Effects of Second-order Hydrodynamics on a Semisubmersible Floating Offshore Wind Turbine[R]. Golden,CO:The National Renewable Energy Laboratory (NREL)，2014.

[9]Jonkman J M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine[D]. Fort Collins:Colorado State University，2001.

[10]Benitz M A，Schmidt D P，Lackner M A，et al. Comparison of Hydrodynamic Load Predictions between Engineering Models and Computational Fluid Dynamics for the OC4-DeepCwind Semi-Submersible[C]//The ASME 2014 33rd International Conference on Ocean，Offshore and Arctic Engineering. San Francisco，California，2014.

(編輯郭偉)

Second-order Hydrodynamics Computation and Response Characteristic Analysis for a Semi-submersible Offshore Floating Wind Turbine

Peng Chunjiang1,2Hu Yanping2Cheng Junsheng1Shen Yiping2

1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University，Changsha，410082 2.Hunan University of Science and Technology，Xiangtan，Hunan,411201

A second-order hydrodynamics computation method was proposed based on the quadratic impulse response function technique for offshore floating wind turbines. Firstly，the quadratic transfer functions were calculated using the direct integration method through three-dimensional potential theory. Secondly，the quadratic impulse response function technique was applied to compute the second-order hydrodynamics in terms of the quadratic transfer functions and wave elevation. Lastly，the resulting second-order hydrodynamics was acted on the integrated dynamics model of offshore floating wind turbine in time domain. So the excitation response of the second-order hydrodynamics might be computed. Taking the DeepCwind semi-submersible platform supporting the NREL 5-MW offshore baseline wind turbine for case，the verification of the second-order hydrodynamics computation method presented was conducted,and various excitation responses were calculated and analyzed. The results show the slow drift force and mean drift force have notable influences on semi-submersible platform，but the sum frequency second-order force can be neglected.

offshore floating wind turbine; semi-submersible floating platform; second-order hydrodynamics; quadratic transfer function; response characteristic

2015-05-21

國家自然科學(xué)基金資助項(xiàng)目(51075131，11572125)

TK83DOI：10.3969/j.issn.1004-132X.2016.07.018

彭春江，女，1977年生。湖南大學(xué)機(jī)械與運(yùn)載工程學(xué)院博士研究生，湖南科技大學(xué)機(jī)電工程學(xué)院講師。主要研究方向?yàn)楹Ｉ细∈斤L(fēng)力發(fā)電機(jī)組動力學(xué)及控制系統(tǒng)。胡燕平，男，1957年生。湖南科技大學(xué)機(jī)電工程學(xué)院教授、博士研究生導(dǎo)師。程軍圣，男，1968年生。湖南大學(xué)機(jī)械與運(yùn)載工程學(xué)院教授、博士研究生導(dǎo)師。沈意平，女，1982年生。湖南科技大學(xué)機(jī)械設(shè)備健康維護(hù)省重點(diǎn)實(shí)驗(yàn)室副教授、博士。