《線性動態系統理論與設計》課程案例化教學改革與實踐

黃景濤 邱聯奎

摘要：在碩士研究生的課堂教學中，案例教學起著重要的作用。本文通過總結在線性動態系統理論與設計課程教學的改革與實踐，提煉和設計了直線二級倒立擺系統教學案例，通過系統原理介紹和任務設計，將課程主要內容有機串聯，為學生學習該門課程提供了一個直觀形象的實物載體，結合案例進行課程教學，改變了該課程理論性強、數學味濃帶來的學生學習困難問題，起到了較好的教學效果。

關鍵詞：線性動態系統；教學改革；案例教學；直線二級倒立

中圖分類號：G642.0 文獻標志碼：A 文章編號：1674-9324（2016）31-0085-03

一、引言

線性動態系統理論與設計是電氣工程、控制科學與工程等學科的專業基礎課程，包括清華大學、浙江大學、斯坦福大學、麻省理工學院等國內外重點大學均開設了類似課程。該課程的研究對象是各種實際系統抽象出來的、形式上具有統一性的具有線性屬性的一類動態系統，借助線性代數和矩陣分析的方法，進行系統分析與控制器設計方法的訓練，培養學生對系統進行數學建模、分析與推理能力，使學生具備利用數學工具對控制系統進行理論描述、系統分析和控制器設計的綜合能力[1-3]。

該課程作為控制科學與工程、電氣工程等學科碩士研究生核心課程之一，以往教學過程主要注重基礎理論和基本方法的講授，作為分析工具的數學在教學過程中所占比例較大。隨著研究生教育規模的擴大，根據地方普通高校研究生的現狀，需要在講授基礎理論和基本方法的基礎上，突出相關理論、方法的工程應用背景[4]。

二、教學案例設計

根據線性動態系統理論與設計課程的特點及在學科中的基礎性，教學案例需要在教學過程中結合學生基礎知識及課程基本理論、方法進行選擇與設計。根據多年的教學實踐，本課程選擇典型的直線二級倒立擺作為教學案例。直線二級倒立擺作為典型的機電一體化抽象模型，是人形機器人等實際系統的物理模型。該系統是一個非線性自然不穩定系統，通過該系統可更直觀地展現動態系統的穩定性、能控性以及系統狀態的收斂速度等抽象概念[3]。由于該系統的典型性，已有大量文獻資料可供參考，便于在Matlab/Simulink仿真環境中分析、驗證，結合實驗室原有的物理實驗裝置，可對線性動態系統的分析、綜合進行實際實驗驗證[5]。

（一）直線二級倒立擺物理模型

直線倒立擺是在直線運動模塊上裝有擺體組件，直線運動模塊有一個自由度，小車可以沿導軌水平運動，從而保持倒立擺系統的平衡與穩定，系統組成如圖1所示。為簡化系統，在建模時忽略了空氣阻力和各種摩擦，并認為擺桿為剛體。

其中，M為小車質量，m1為擺桿1的質量，m2為擺桿2的質量，m3為質量塊的質量，l1為擺桿1中心到轉動中心的距離，l2為擺桿2中心到轉動中心的距離，θ1為擺桿1與豎直方向的夾角，θ2擺桿2與豎直方向的夾角，F為作用在系統上的外力。

三、案例化教學方式實踐

結合實例在建立系統狀態空間模型后，可基于該系統模型對系統的能控性、能觀測性等進行分析，在課程內容的運動分析、能控性、能觀測性以及穩定性分析相關的基本理論與方法時，結合該系統進行講解，使抽象的、數學化的理論方法具有明確的物理含義，便于學生理解與掌握相關原理、方法。

1.系統開環仿真。結合該案例，要求學生利用Matlab/Simulink仿真環境建立系統模型，并進行相關算例的編程計算、系統分析。系統的Matlab/Simulink模型如圖2所示。

其中“State-Space”模塊為直線兩級倒立擺的狀態方程，雙擊模塊可打開模型進行參數設定。

建立好系統仿真模型后，對系統進行開環仿真，仿真結果如圖3所示。從仿真結果可以看出，系統發散，為使系統穩定，需要對其添加控制器。

2.控制器設計與仿真。為使系統穩定，需要針對該系統設計閉環控制器，采取狀態反饋的形式進行控制器設計，控制率采用線性二次型最優控制（LQR）方法，仿真模型如圖4所示。根據LQR控制方法的原理，可計算出控制器狀態反饋矩陣的參數為K=[1 73.818 -83.941 2.0162 4.2791 -13.036]，仿真結果如圖5所示。

由圖5可見，系統雖然可以穩定，但系統穩定時間過長，根據LQR的基本原理，可知要增加系統響應速度，需增加權重Q的值。

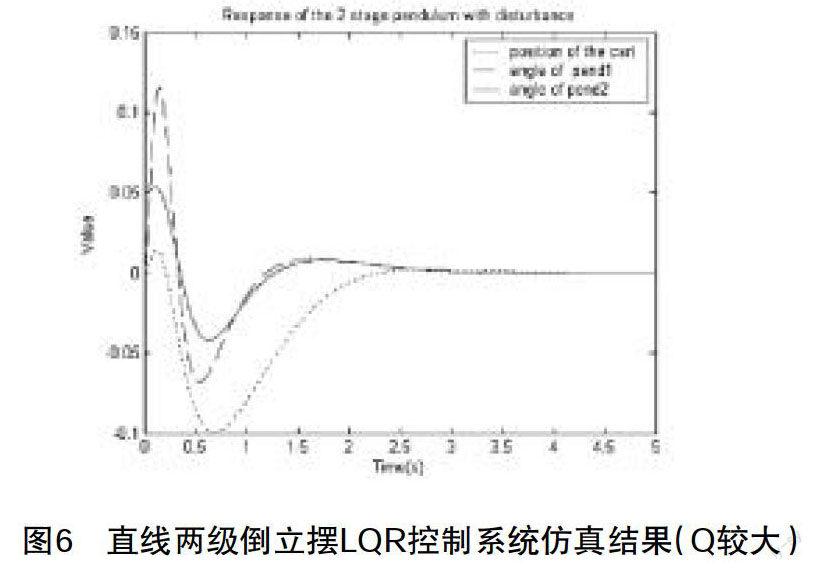
設Q11=300，Q22=500，Q33=500，對應的LQR控制器參數為K=[17.321 110.87 -197.57 18.468 2.7061 -32.142]，仿真結果如圖6所示。

由圖6可以看出，系統可以很好的穩定，在給定倒立擺干擾后，系統在2.5秒內可以恢復到平衡點附近。通過對參數的重新設置，觀察仿真結果，進而加深對相應控制方法的理解和掌握。

3.實時實驗驗證。根據上述仿真結果，選取具有較好響應的控制器參數進行實時控制實驗，對比驗證控制方法在實際系統上的控制效果，由于實際系統存在干擾信號、檢測信號噪聲、機械摩擦等實際情況，一般而言，實物系統上的控制效果與仿真結果會有一定差異。

實物實驗驗證在實驗室的直線二級倒立擺平臺上進行，控制算法仍可基于Matlab/Simulink進行。實時控制系統如圖7所示。

四、結論

案例化教學方式的實施，除了教學案例的引入、課程教學組織的變化，學生的深度參與對于教學效果更為重要，在教學過程中要求學生在仿真環境中自行建立系統模型，對系統性質進行分析，在此基礎上，嘗試設計控制器，可覆蓋課程大部分內容，通過案例將各知識模塊和方法有機聯系在一起，使學生進一步明確課程內容對于實際系統的作用，一方面可提升學生學習的目的性、積極性，同時訓練了學生分析問題、解決問題的能力。

參考文獻：

[1]鄭大鐘.線性系統理論[M].第2版.北京：清華大學出版社，2002.

[2]Chi-Tsong Chen. Linear system theory and design，3rd edition. New York：Oxford University Press，1999.

[3]王曉蘭，李恒杰.“線性系統理論”課程教學案例的設計[J].電子電氣教學學報，2013，35（2）：21-23.

[4]齊曉慧，王永川，董海瑞.研究生“線性系統理論”課程教學改革與實踐[J].中國電力教育，2010，（32）：82-84.

[5]高榮，劉曉華.線性系統理論教學改革探討與實踐[J].中國科教創新導刊，2008，（30）：85.