淺談如何在教學中滲透數學模型思想

【摘要】小學數學建模思想的形成過程是一個綜合性的過程，在數學教學過程中進行數學模型思想的滲透至關重要，可以加深學生對數學知識與方法的理解和掌握，培養學生應用數學的意識與能力。在數學課堂教學中，教師應重視滲透數學模型思想，讓學生在進行探究性學習的過程中科學地、合理地、有效地建立數學模型。

【關鍵詞】模型思想 小學數學 課堂教學 滲透策略

【中圖分類號】G623.5 【文獻標識碼】A 【文章編號】2095-3089（2016）07-0127-02

《數學課程標準》提出：讓學生親身經歷將實際問題抽象成數學模型并進行解釋與應用的過程，進而使學生獲得對數學理解的同時，在思維能力、情感態度與價值觀等多方面得到進步和發展。這實際上就是要求把學生學習數學知識的過程當做建立數學模型的過程，并在建模過程中培養學生的數學應用意識，引導學生自覺地用數學的方法去分析、解決生活中的問題。明確要求教師在教學中引導學生建立數學模型，不但要重視其結果，更要關注學生自主建立數學模型的過程，讓學生在進行探究性學習的過程中科學地、合理地、有效地建立數學模型。下面我結合自己的教學實踐體會，談談如何在數學教學中滲透數學模型思想。

一、創設情境，感知數學建模思想

數學來源于生活，又服務于生活，因此，要將現實生活中發生的與數學學習有關的素材及時引入課堂，要將教材上的內容通過生活中熟悉的事例，以情境的方式在課堂上展示給學生，描述數學問題產生的背景。情景的創設要與社會生活實際、時代熱點問題、自然、社會文化等與數學問題有關的各種因素相結合，讓學生感到真實、新奇、有趣、可操作，滿足學生好奇好動的心理要求。這樣很容易激發學生的興趣，并在學生的頭腦中激活已有的生活經驗，也容易使學生用積累的經驗來感受其中隱含的數學問題，從而促使學生將生活問題抽象成數學問題，感知數學模型的存在。

在教學數學廣角“田忌賽馬”一課，新課伊始，我首先進行“撲克牌比大小，三局兩勝就算嬴”的活動。

1.出示兩組牌，第一組牌是（9 7 5），第二組牌是（3 2 1）

第一次與學生PK。讓學生先選一組牌，學生將會很自然選大牌，第一次按從大到小的順序出牌，輸了。

師：唉，三局全輸了，我換換出牌的順序，再來。

第二次與學生PK。

師苦惱說：還是三局都輸了。為什么我總是輸呢？

生：老師三張牌都比我們最小的牌小，不可能贏的。

師：原來是我的牌太差了，兩組牌實力相差太遠，勝負明顯。

2.師：既然這組牌一定全輸，那我把（3 2 1）換一組撲克牌，就取（8 6 4）吧！并問：你想取哪組牌。

將預設出現以下A與B兩種情況：

A、學生選（9 7 5）、教師選（8 6 4）的情況：

（1）師：你為什么選（9 7 5）

生：實力較強

師：那我會不會又是全輸呢？我想試試。

（2）讓學生先出，教師故意輸三局

師：哎呀，又是全輸！我再想想辦法。

同樣由學生先出牌，故意只贏一局。

師：哈哈，終于贏一局了，我再想想能不能贏你。

再由學生先出牌，贏兩局。

引導出是用了一種可以以弱勝強的對策——田忌賽馬的對策。

B、學生選（8 6 4）、教師選（9 7 5）的情況：

（1）師：你為什么選（8 6 4）？你要知道我的實力較強一些喲？

讓學生先出，教師贏兩回后問：你們有辦法贏我嗎？（如沒有學生回答，教師與學生換牌），教師讓學生先出，結果贏兩局輸一局勝出，學生詫異！

引導出是用了一種可以以弱勝強的對策——田忌賽馬的對策。

以上學生在多次對弈中理解、分析與整理數據，產生思維沖突，從而推進數學思考的有序進行。學生從具體的問題情境中抽出以弱勝強的對策這一數學問題的過程就是一次建模的過程。

二、參與探究，主動建構數學模型

數學家華羅庚先生通過多年的學習、研究經歷總結出：對書本中的某些原理、定律、公式、方法以及對策，我們在學習的時候不僅應該記住它的結論、懂得它的道理，而且還應該設想一下人家是怎樣想出來的，怎樣一步一步提煉出來的。只有經歷這樣的探索過程，數學的思想、方法才能沉積、凝聚，從而使知識具有更大的智慧價值。動手實踐、自主探索與合作交流是學生學習數學的重要方式。學生的數學學習活動應當是一個主動、活潑、生動和富有個性的過程。因此，在教學時我們要善于引導學生自主探索、合作交流，對學習過程、學習材料、學習發現主動歸納、提升，力求建構出人人都能理解的數學模型。

在教學 “田忌賽馬”一課，我充分挖掘教材資源，大膽的嘗試把文本故事中的數學信息轉變成數學模型，并用數學的方法表達故事的對策。

首先，在讓學生收聽故事并觀察屏幕中的關鍵信息后，我讓學生分析第一次輸了以及第二次又贏了的原因？跟著引導學生根據文本，思考田忌所用的這種策略是不是唯一能贏齊王的方法？田忌共有多少種可采用的應對策略呢？接著，我大膽嘗試讓學生思考從撲克牌1-9中選出六張分別來代替齊威王與田忌的上、中、下等馬去研究，并讓學生根據故事文本敘述所用數字代替的合理性，促使學生把故事里的數學信息用數學的辦法呈現出來，并利用直觀的數字采用數學的方法去研究田忌所有的可采用的應對策略。這個數學的方法其實就是用三個數字組成三位數的方法，并在其中滲透有序的思想，整個過程，我力求把文本中的數學信息轉變成數學模型進行研究。

在探究“田忌賽馬”獲勝的必要條件有哪些的時候？我意識到“田忌賽馬”不僅僅是一個故事，而是一種策略。這一策略并不是“必勝寶典”，而是需要一定的前提。但在教學中如果僅依賴“田忌賽馬”的故事本身，不利于學生從對策論的角度進行探究。因此，我再次在教學中提供與“田忌賽馬”同樣結構的探究材料（所代替撲克牌），讓學生扮演田忌與扮演齊王的教師進行對弈，通過不斷的嘗試、發現、概括、歸納。從而充分理解 “實力稍弱，智者勝”的具體對策和獲勝的必要條件。

這一環節的設計，不僅發展了學生的策略性知識，同時讓學生經歷猜測與驗證、分析與歸納、抽象與概括的數學思維過程，充分體驗了數學模型的形成過程。

三、解決問題，拓展應用數學模型

用所建立的數學模型來解答生活實際中的問題，能讓學生體會到數學模型的實際應用價值，體驗到所學知識的用途和益處，可以進一步讓學生在實際應用過程中認識新問題，同化新知識，并構建自己的智力系統，同時讓學生體驗實際應用帶來的快樂。

如在學生掌握了田忌賽馬對策問題后，我設計了這樣的練習題：

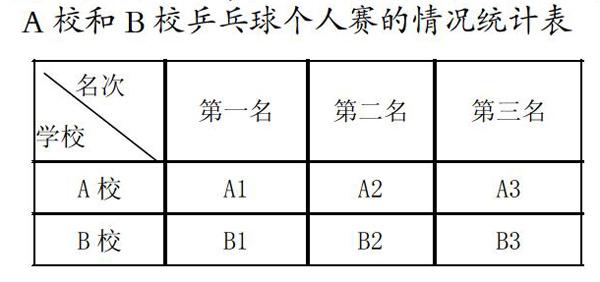
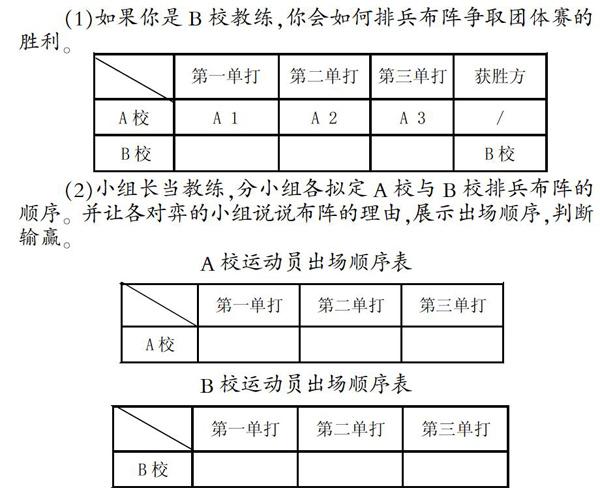
在我們的生活中，經常用到田忌賽馬的對策，如在體育比賽中，A校和B校乒乓球個人賽，同一名次的選手實力相當，但第一名的都能打贏第二名，第二名的都能打贏第三名。 學生在掌握了田忌賽馬對策問題這一模型后，通過進行如上的變式練習，學生易于形成實事求是的態度以及進行質疑和獨立思考的習慣，激發學生的創新精神。因此，我們在教學過程中，應注重學生建模思想的形成與運用。

綜上所述，小學數學建模思想的形成過程是一個綜合性的過程，是數學能力和其他各種能力協同發展的過程。在數學教學過程中進行數學建模思想的滲透，不僅可以使學生體會到數學并非只是一門抽象的學科，而且可以使學生感覺到利用數學建模的思想結合數學方法解決實際問題的妙處，進而對數學產生更大的興趣。通過數學模型思想的滲透，可以加深學生對數學知識和方法的理解和掌握，調整學生的知識結構，深化知識層次。同時，培養學生應用數學的意識和自主、合作、探索、創新的精神，為學生的終身學習、可持續發展奠定基礎。因此在數學課堂教學中，教師應逐步培養學生數學建模的思想、方法，形成學生良好的思維習慣和用數學的能力。

參考文獻：

[1]許衛兵.磨·模·魔———小學數學教學中滲透模型思想的思考[J].課程·教材·教法，2012（1）：89-94.

[2]俞小燕.小學數學教學中數學模型思想的融入[J].讀與寫（教育教學刊），2013，（12）：225.

作者簡介：

潘鋒明（1978，7-），男，漢族，廣東從化人，本科畢業，中級教師，從化區小學數學教研會副會長，廣州市小學數學教研會常務理事。