數形結合深挖內涵明晰概念

朱東亮

[摘 要]數學概念是構建數學理論大廈的基石，是數學學科的靈魂和精髓。因此，教師應重視概念教學，通過數形結合等途徑，引導學生深入挖掘概念的內涵，明晰所學的概念，真正掌握所學的知識。

[關鍵詞]概念教學 平均數 思維沖突 價值 幾何直觀 意義 內涵 特性

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2016）23-032

對概念清晰而又深刻的理解是學好數學的關鍵，是應用數學知識解決問題的基礎。平均數是一個重要的刻畫數據集中趨勢的統計量，小學數學中所講的平均數一般是指算術平均數，也就是一組數據的和除以這個數據的個數所得到的商。平均數既可以反映一組數據的一般情況，也可以用它進行不同組數據的比較，從而看出組與組之間的差別。下面，我以“平均數”一課教學為例，嘗試探討概念教學的方法。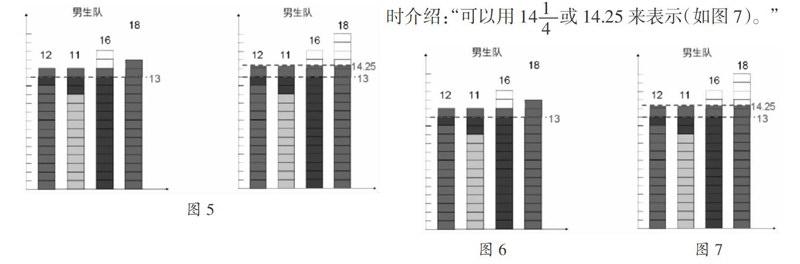

一、設置思維沖突，體會平均數的價值

學生對通過比較總數判斷兩組數據水平的高低有著豐富的經驗，因此，教師教學時可以先出示圖1，讓學生判斷在踢毽子比賽中哪個隊獲勝。然后教師參加到男生隊中（師踢了13個），并提問“通過比較總數來判斷哪個隊獲勝公平嗎”，以激發學生的思維沖突，引導學生提出用平均數來判斷。雖然平均數是一組數據本身就具有的屬性，不依賴于比較存在，但根據學生的思維水平和特點，采用這樣的引入方式可以讓學生充分感受到比總數的局限性，體會到平均數產生的必要性和價值。這對激發學生學習概念的興趣，比較不同概念之間的聯系與區別有著重要作用。

二、利用幾何直觀，理解平均數的意義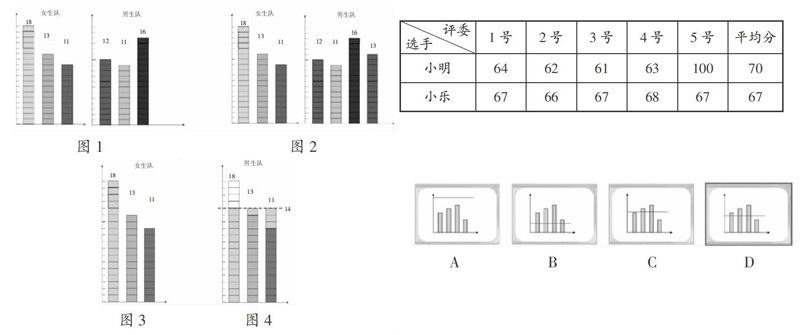

華羅庚說過：“數缺形時時少直觀，形缺數時難入微。”“平均數”一課的教學，可采用數形結合的方式進行。平均數是刻畫數據集中趨勢的統計量，反映了一組數據中心點的位置所在，這是平均數統計意義的核心。因此，讓學生經歷一組數據中心點的產生過程，有助于學生理解平均數的概念。具體可以采用“移多補少”的方法讓學生體會這個過程：3名女生踢毽子的個數如圖3，通過計算得出女生隊踢毽子的平均數是14個。然后引導學生通過“移多補少”的方法找到平均數，再將平均數直觀地展現在學生眼前，如圖4。通過圖形的直觀展示，學生對平均數的產生過程有了切實的體會，從而對平均數反映一組數據的一般水平也就有了更深刻的認識。

三、挖掘概念內涵，明晰平均數的特性

根據平均數的概念，平均數具有某些與生俱來的特性，主要包括敏感性、集中性、虛擬性三個方面。通過適當的學習材料，讓學生明晰平均數的特性，有助于學生加深對概念的理解。

1.敏感性

平均數的敏感性是指每個數據的變化都對平均數產生影響。教師可以通過改變其中一個數據的大小，讓學生體會這一特性。如在數據12、11、16、13中，如果將13變成17，那么平均數將從13變成14，使學生明確當個體數據變大時，平均數將被拉升；反之，平均數將被拉低。從平均數的敏感性，教師還可以引導學生發現平均數容易受極大（小）值的影響。如下表中小明的平均分顯然受到100分的影響，從而拉高了平均數。這樣可讓學生體驗到平均數的局限性，了解生活中經常采用去掉部分極值后再求平均數的原因。

2.集中性

平均數的集中性是指平均數一定介于最大值與最小值之間，理解這點有助于學生理解平均數作為集中量數的原因。那么，如何讓學生體會平均數的集中性呢？教師可提供以下材料，并提問：“下圖中，哪幅圖中的線代表了這組數據的平均水平？”通過問題引導學生根據平均數的意義和“移多補少”的方法進行辨析，明確平均數不會比最大值還大，也不會比最小值還小，因為這不符合平均數的概念。而對選項D，則要通過更加細致的辨析，讓學生了解“移多補少”的結果是各個數據均等，從而對平均數有更深入的認識。

3.虛擬性

由于平均數是通過“移多補少”得到的量，因此平均數代表的是這組數據的一般水平，不代表數據中的個體。如圖5中，女生隊踢毽子的數量為18、13、11個，這組數據的平均數是14，這個14不是任何一個女生踢毽子的數量。

另外，學生沒有學過分數除法和小數除法，對平均數是分數（小數）存在著認知障礙，這是正常的現象。如果教師教學時能打破這一障礙，將對學生理解平均數的虛擬性大有裨益。結合圖5，教師可以這樣向學生設問：“如要使男生隊獲勝，老師至少踢幾個？”這是一個極富挑戰性的問題，教師要給足學生思考的時間和交流的機會。教學中，學生提出“老師至少要再多踢8個毽子，這樣才能使男生隊的平均數達到15個，比女生隊的平均數高1個”。有這種想法的學生是需要鼓勵的，因為他們有著較強的分析能力，能從問題出發找到答案。

此時，教師可進一步啟發學生：“還有更好的方法嗎？”一生提出“只要再多踢5個毽子就行了（如圖6）”，此時男生踢毽子的平均數已經達到14個，而且還多出1個。這時有學生質疑：“這多出的1個怎么辦？這樣是不平均的。”教師可追問：“你有辦法將這多出的1個繼續平均分嗎？”通過問題，引導學生將這1個再平均分成4份。由于學生在學習分數時已經有了類似的經驗，所以這時學生發現平均數不是整數了。“那改用一個怎樣的數表示呢？”由于學生沒有學過帶分數和小數，教師可適時介紹：“可以用14或14.25來表示（如圖7）。”

通過一系列問題的提出與解決，學生茅塞頓開，對平均數的敏感性和虛擬性有了進一步的認識，在解決思維障礙的同時，對所學概念有了更加深刻的印象。

總之，教師應重視概念教學，通過數形結合等途徑，引導學生深挖概念的內涵，明晰所學的概念，真正掌握所學的知識。

（責編 杜 華）