淺析教材中“平均分”出現歧義的原因

卻立泉 童小艷 葉嬉嬉

[摘 要]教材是教師教授知識，學生認識新事物和學習新知識的重要載體。課堂教學中，學生對教材呈現的“平均分”提出了異議，追根溯源，并非學生的認知出現了偏差，而是教材的編排引發歧義。

[關鍵詞]教材 平均分 歧義 面積 體積

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2016）26-024

“平均分”與平均數不同，是分物時所用的一種思想，指在分物體的時候要盡可能地分完，而且要使每一份得到的數相等。下面，我就從“平均分”的表示方法入手，分析、探討教材中“平均分”出現歧義的原因。

一、“平均分”的表示方法

1.用面積（或體積）表示的“平均分”（如下圖）

這里，圖形涂色的部分很直觀，很容易理解，符合學生的一般認知規律。

2.用數量表示的“平均分”

關于單純的數量上的平均分，在平時的生活中常常遇到，學生也比較容易理解。

3.“面積”或“體積”和數量同時存在的情況

對于這道題的回答，學生出現了不同的觀點。有的學生說：“把6個蘋果看成一個整體，平均分成了3份，就是平均分！”有的學生則重復著“標準答案”，而大多數學生則跟著點頭認可。也有的學生說：“老師，這不是平均分！”學生經過一番討論，最終提出異議的學生被占優勢的“標準答案”所淹沒。

二、通過調查分析，“平均分”出現分歧的情況確實存在

為什么會有學生認為這不是平均分呢？依據是什么？我課后進行反思，并設計了兩道題（如下圖），對上過此課的三個班級隨機各抽取一個組（合計34人）進行測試和調查。

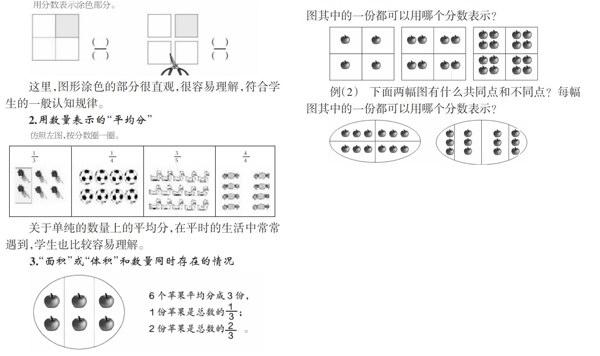
例（1） 下面三幅圖有什么共同點和不同點？每幅圖其中的一份都可以用哪個分數表示？

例（2） 下面兩幅圖有什么共同點和不同點？每幅圖其中的一份都可以用哪個分數表示？

調查結果顯示：例（1），共同點是都把相應的蘋果平均分成了四份，其中的一份都可以用四分之一來表示；不同點是每幅圖的蘋果總數不同，所以每份的蘋果個數也就不同。對于例（1），學生回答的正確率為100%。例（2），學生的回答出現了分歧，有10名學生雖然迅速地說出第一幅圖平均分成了四份，其中的一份可以用四分之一表示，但是他們對第二幅圖的第一反應卻說不是平均分成了四份，棄用四分之一而選用十二分之三來表示其中的一份。這是由于學生無法領會集合圈這一數學符號的意思，故不用四分之一而選用十二分之三來表示。這不得不引起我們教師的深思：在平時的授課中，我們應該用什么樣的方式，把知識更好地傳授給學生，讓他們能更好地理解所學的知識？

三、“平均分”出現分歧的原因總結

針對教材“面積”或“體積”和數量同時存在的這種編排設計，我翻閱了多種同類知識的教材版本，發現蘇教版和北師大版教材均未出現人教版教材中這種“積（面積、體積）”“物（數量）”重疊的編排設計。這樣編排的設計意圖是讓學生體會單位“1”，培養學生的符號意識，但是卻不符合學生的認識規律，容易造成學生認知混亂。若非要“積”“物”重疊的設計，可以把集合圈換成矩形或圓形，這樣無論是從“積（面積、體積）”，還是從“物（數量）”方面進行觀察，都能做到等量齊觀，會更符合學生的認知規律。

張奠宙教授曾對小學數學教材提出五點建議：一是必須堅決杜絕錯誤；二是保持數學的準確性特點；三是把教學的重點放在解釋數學的本質上；四是數學的科學性需要用數學思想方法加以體現；五是要做到與時俱進，不斷變化。同時，我也斗膽提一點建議，那就是教師應尊重學情，遵從學生的認知規律，循序漸進地進行教學。

（責編 藍 天）