在圖形與幾何教學中培養遷移能力

浙江寧波市鄞州區下應街道中心小學（315104）　俞孟立

在圖形與幾何教學中培養遷移能力

浙江寧波市鄞州區下應街道中心小學（315104）俞孟立

幾何圖形間都存在著非常緊密的聯系，如果單獨對一塊知識點組織教學，割裂了知識點之間的聯系，會造成學生對概念的認識片面化，不利于學生學習能力的培養。教師如果能根據幾何圖形間的內在聯系巧妙組織教學，就能有效培養學生的知識遷移能力。

幾何圖形知識遷移類比對比舉一反三

知識遷移是“一種學習對另一種學習的影響”，是根據自身的經驗背景，對外部信息進行主動地選擇、加工和處理等過程。在圖形與幾何的課堂教學中充分運用遷移規律，實現知識的有效遷移，是教學成功的一個重要環節。學生形成較好的知識遷移能力后，可以避免死記硬背，實現知識點之間的貫通理解和轉換，有助于認識事物的本質和規律，從而構建知識結構網絡，提高解決問題的靈活性和有效性。

一、加強聯系，以類比促遷移，實現遷移通暢

知識遷移的產生與前后知識之間的相同因素和相互關系有關。只有找出新舊知識的內在聯系，學生才能將知識進行遷移。因此，教師在教學中要引導學生對已經學習過的知識進行回顧和總結，找出兩者的內在聯系，使學生可以自主地鏈接新舊知識，引導學生由此及彼，以舊學新，突破難點，掌握新知。

如教學“三角形的高”時，可以平行四邊形的高為橋梁，通過類比，順勢關聯新知。

【鏡頭重現：三角形高的定義及作高】

1.出示平行四邊形。利用課件動態演示平行四邊形到梯形再到三角形和三角形到梯形到平行四邊形的變化過程。

①復習平行四邊形的高，課件演示作高的過程，讓學生拿起尺子跟著電腦一起作高，教師在一旁提示：“一條直角邊與底重合，另一條直角邊為過某個點的垂線。”

②給出概念：從平行四邊形一條邊上的一點到對邊引一條垂線，這個點和垂足之間的線段叫做平行四邊形的高，垂足所在的邊叫做平行四邊形的底。

③在平行四邊形的一條邊上取一點與其對邊的兩個端點連成三角形。如果以此邊為底，三角形的高應該怎么畫？

④你覺得三角形的高指的是什么？根據剛才的研究，三角形有三個頂點、三條邊，可以畫幾條高？

2.遷移引導：你能不能根據平行四邊形高的定義，類推出三角形高的定義？

3.概括高的意義：點到對邊的垂線段。

在學習三角形的高之前，學生已經認識了三角形，通過變一變，動態中促進了平行四邊形、梯形、三角形在數學本質屬性上的聯系。打通圖形之間的聯系，使學生意識到高并不是新事物，而是原先學過的舊知，用這樣的“似曾相識”類推出三角形畫高的方法。這樣以類比促遷移，以舊學新，突破難點，學生不僅順利掌握了新知，而且培養了知識遷移的能力。

二、辨析異同，以對比促遷移，克服思維定式

思維定式是指先于一定活動而指向該活動的一種準備狀態。它有時會產生消極性影響，導致知識負遷移，從而影響學生理解和掌握知識。所以在發展遷移能力的過程中，要通過直觀對比，把握各知識點的異同點。

如在教學“平行四邊形面積”時，學生會受長方形面積計算方法的影響，出現負遷移。這就需要通過對比和動手操作去發現它們的不同點，消除消極影響，形成求異的意識與能力。

【鏡頭重現：平行四邊形的面積】

師（出示教具）：這是一個長方形框架，它的長是7厘米，寬是5厘米，它的面積是多少？你是怎樣思考的？

（復習長方形面積的計算方法，根據學生的回答，教師板書：長方形的面積=長×寬）

師：如果捏住這個長方形的3一組對角，向外拉（如右圖），大家看看，它現在變成了什么圖形？（平行四邊形）

師：請你猜想一下平行四邊形面積的計算公式。

（相當一部分學生受長方形面積計算方法的干擾，認為平行四邊形的面積等于相鄰兩條邊的乘積，但也有學生提出四邊形的面積等于底乘高。）

師：究竟哪種猜想是正確的？下面利用手中的學具袋（袋中裝有一個底是7厘米，鄰邊5厘米，高3厘米的平行四邊形），小組合作，驗證一下。

生A：長方形框架拉得越扁，面積就越小，所以平行四邊形的面積等于相鄰兩條邊的乘積是錯誤的。

生B：通過數格子，我發現平行四邊形的面積等于底乘高。

生C：通過剪一剪、拼一拼，我發現平行四邊形的面積等于底乘高。

當遷移能力發展到一定程度時，學生會出現思維定式，教師要及時地進行引導，通過對比等方法直觀呈現，讓學生克服定式思維。這要求學生對問題進行再處理、再變換，或嘗試與另一認知結構對接，從不同角度分析、遷移知識解決問題，而不是生搬硬套。所以，具體問題要具體分析、具體處理，形成求異思維的意識與能力。

三、舉一反三，以發散促遷移，實現遷移多元

遷移能使知識點構成一個有機的整體，在新舊知識間建立起實質性的聯系，使新知識、新問題納入到原有的認知結構中，形成知識網絡。舉一反三正是從“一”到“三”的發散過程，發現一類題的共性和表現形式，從而達到由會解這道題上升到會解這類題的境界。

如在教學長方形、正方形、平行四邊形、梯形、三角形、圓的面積公式時，學生一般都采用單獨記憶的方法，但如果通過遷移將這五種圖形的面積公式概括為一個通用公式，就可以迅速將所有的公式記憶下來，減輕記憶的負擔。

【鏡頭重現：平面圖形面積的復習整理】

師（復習回顧）：我們學過哪些基本的平面圖形？它們的面積計算公式是什么？用字母怎樣表示？（生逐一回答，并說明公式中的字母各表示什么。）

師（梳理推導公式）：這些平面圖形的面積計算公式之間有怎樣的聯系呢？

生：把長方形看成上底與下底相等的梯形，可用梯形面積公式推導長方形的面積公式：S=（a+a）×b÷2=2a× b÷2=ab。

師（舉一反三）：梯形面積公式可推導出長方形的面積計算公式，你能用梯形面積公式推導出其他圖形的面積計算公式嗎？

（經過知識遷移，舉一反三，學生很快發現正方形、長方形、梯形、三角形、圓形面積公式的共性：仍是面積等于上底與下底之和乘高除以2，如下圖所示。）

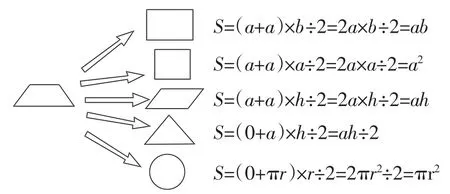
（注：把圓看作上底為0，下底為周長，高為半徑的梯形）

學生以長方形與梯形的面積計算公式間的聯系為橋梁，通過舉一反三，類推出其他平面圖形的面積公式，實現知識的發散性遷移。經常進行這樣的思維訓練，學生就能將知識點靈活轉換和應用，由會解這道題變為會解這類題，實現知識遷移能力多元化發展。

總之，在進行圖形與幾何的教學中，教師要經常讓學生通過類比、對比、舉一反三等活動充分運用遷移規律，實現知識的有效遷移。當學生較好的形成知識遷移能力后，可以實現知識點之間的貫通和轉換，有利于認識事物的本質和規律，構建知識結構體系，提高解決問題的靈活性和有效性，形成并提升知識遷移能力。

（責編吳美玲）

G623.5

A

1007-9068（2016）29-068