高中信息技術與數學算法教學整合的若干思考

黃求標（泰寧第一中學，福建泰寧354400）

高中信息技術與數學算法教學整合的若干思考

黃求標
（泰寧第一中學，福建泰寧354400）

高中數學算法教學普遍存在“紙上談兵”的問題，應用計算機輔助軟件制作程序框圖十分簡單，能編譯為可執行文件運行，立即檢驗算法是否正確，非常適合高中師生講解或研習算法使用。

算法教學；程序框圖；程序代碼；編譯

在普通高中數學課程標準中，算法模塊中要求學生通過模仿、操作、探索，學習設計程序框圖表達解決問題的過程；體會算法的基本思想以及算法的重要性和有效性，發展有條理的思考與表達的能力，提高邏輯思維能力［1］。教育部《普通高中數學課程標準（實驗）》在闡述高中數學課程的基本理念時，明確指出，當今知識經濟時代，計算機技術與數學相融合，正在對數學課程內容的組織和呈現方式、數學教學的過程與方法產生深刻影響。教師應盡可能使用各種教育技術手段，加強數學教學與信息技術的融合，鼓勵學生運用信息技術手段進行探索與發現學習。

一、算法教學存在的問題

算法作為具體的教學內容進入中學數學的教科書中，讓一些數學教師覺得難以適應，算法教學該如何開展，學生如何學習算法，這些問題擺在了每一個高中教師的面前。信息技術作為一種現代教學手段如何更好的服務教學，提高教學效果。然而，放眼高中數學算法教學課堂，會發現存在諸多問題：

1.教師的算法水平和實現能力偏低，只會“紙上談兵”

算法是高中數學新課改課程新增內容。許多一線高中數學教師，尤其是年齡較大的教師，求學期間沒有系統學習過算法，在職培訓也沒有及時有效跟進，他們缺乏在計算機上驗證程序的意識和能力，一般只能機械地講講程序框圖，只會“紙上談兵”式地模擬計算機執行程序框圖，幾乎從不安排學生集體上機實踐，從而將本來實踐性強、生動有趣的內容變成了機械呆板、枯燥乏味的說教。

2.“固化”“機械”的高考題型助長了教師的“紙上談兵”

由于許多省市高考似乎就只考“根據程序框圖寫出程序運行結果”這種題型，而且往往只需照著框圖模擬運行幾趟（一般是3至6趟）就能直接得到結果，這種極端機械的題型，使得大部分一線數學教師和學生堅信只需“紙上談兵”即可，從而大大削弱了算法教學。

3.算法教學存在兩大“結構性”障礙，讓師生止步于“紙上談兵”

⑴分析問題時，得到了用自然語言表示的解題步驟，然后把它轉化為程序框圖，那么怎么實現這個“轉化”？無論是在紙上還是在黑板或白板上畫，無論用鉛筆還是粉筆或白板筆或者用Word、Visio軟件畫程序框圖，都費時費力！

⑵好不容易畫出程序框圖后，再怎么轉化為程序？這個框圖是給人看的，是人與人之間交流算法思想時用的，根本不能由計算機運行，只能用于紙上談兵式的手工模擬！只有將它轉換為程序，才能由計算機執行。由于學生先學程序框圖，還不會寫代碼，因此無法寫出代碼驗證算法。如果先學算法語句，學會編寫程序代碼，則又淡化了算法思想的主導作用，違背了算法教學的初衷：重在理解算法思想，不要上成程序設計課，這就是算法思想與程序實現之間的結構性矛盾：從邏輯上講，先有算法思想，再編程實現；但從技術上講，先要編寫程序，運行程序才能實現算法檢驗算法——這樣就陷入了類似于先有“雞”還是先有“蛋”的“怪圈”。

離開算法的計算機實現，在紙上空談算法是荒謬的。那么，如何激活機械呆板、死氣沉沉的算法教學呢？歸根到底，算法就是人們為了便于用計算機解決問題而創設的數學運算模型，由于上述諸多原因，倒在了離它被實現被實證的“最后一米”！傳統數學課堂的“師-生”（或“師-演示電腦-生”）模式無法逾越這道“數字鴻溝”，必須引入“生-機（電腦）”模式，用信息技術破解本來就屬于信息技術范疇的算法教學的困境，為算法思想的實現插上飛翔的翅膀。

算法最直觀形象的表示方法就是流程圖（即程序框圖），因此，流程圖就是高中算法教學的“牛鼻子”！無論用什么工具畫流程圖，畫出來的圖都是“死”圖，這個圖不能象真正的程序一樣由計算機運行，是否正確只能在紙上模擬。一個能精確表示算法的流程圖，卻不能成為真正可運行的程序，從而使算法教學嚴重依附于程序設計，成為其附屬物，甚至累贅！這導致兩種后果：一是象數學上的算法課那樣，算法的“實現”用紙上談兵式的手工“模擬”代替（純講算法，忽視實現），二是像信息技術課程中的程序設計那樣，把“雞肋”似的算法直接忽略（講了程序，算法就顯得多余）！

二、信息技術在數學算法教學上的運用

學習算法，關鍵在于編寫出讓計算機執行的程序。看到計算機執行自己的程序并快速準確地給出問題的解答，會讓學生體會到學習算法的成就感；另一方面，若執行程序未得到自己預期的答案，則可以對自己的算法和程序進行檢查，

通過實踐中的問題學習算法可以加深對算法及程序的認識和理解［2］。如果在算法課堂上，學生用拖拽圖標的方式輕松地繪制流程圖，系統自動生成程序代碼，這樣就使流程圖成為可執行的“活”圖，算法就成為可立即運行檢驗的“活”思想，那么學生在研究、設計算法時，就暫時不必理會程序語言代碼和實現的細節，只需專注于算法思想，這樣就大大降低了算法入門的門檻，算法就可以獨立于程序設計，而成為程序設計的先導內容，真正成為程序的靈魂。顯然，高中師生需要這樣的工具平臺，來輔助解決兩個問題：一是快捷方便地繪制程序框圖，二是自動編程實現算法驗證算法。

算法是求解某一類問題所采用的一組定義明確、操作有序的步驟。通俗地說，就是計算機解題的過程。對算法進行描述，通常可以使用自然語言、程序框圖、程序代碼等方式。

例如，用計算機來計算圓的面積，即用自然語言描述算法［3］：

第1步：用戶要把圓的半徑r的值告訴計算機，即輸入圓的半徑r；

第2步：計算機用公式S=πr2計算圓的面積（圓周率也要明確告知計算機）；

第3步：計算機要把圓的面積S的值反饋給用戶，即輸出圓的面積S。

這種用自然語言描述的算法不直觀，有時可能還有歧義，計算機也不明白人類的語言。于是，人們就想出了另外一種形式——用一種特定的圖形把算法直觀、準確地表達出來，這就是程序框圖。啟動軟件，“流程圖窗口”中會自動創建了一個“最簡單”的程序框圖：一個“開始”圖標和一個“結束”圖標，在這兩個圖標之間有一條“流程線”，如圖1所示。用軟件計算圓的面積操作如下。

第1步：輸入圓的半徑。點擊“圖標工具箱”，選擇“輸入”圖標（平行四邊形），按住鼠標左鍵拖拽到流程線上，至出現虛線框時釋放左鍵，插入一個“輸入”圖標。輸入字母r，表示圓的半徑（為嚴謹起見，向圖標內鍵入的內容在文章中一律加下劃線表示，實際錄入時則不必加下劃線）。

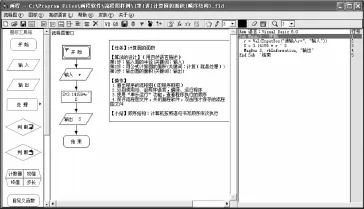
圖1 用畫程軟件繪制“計算圓的面積”程序框圖

第2步：用公式計算圓的面積。點擊“圖標工具箱”，選擇“處理”圖標（矩形），拖拽一個“處理”圖標到流程線上，在圖標里面輸入計算圓的面積的公式：S= 3.14159*r^2，變量S表示圓的面積，圓周率π直接給出常數3.14159，乘號用“*”號表示，r是半徑，乘方符號“^”是主鍵盤數字6的上檔鍵，按住Shift鍵不放，再按下6，這樣就輸入了乘方符號“^”。

第3步：輸出圓的面積。點擊“圖標工具箱”，選擇“輸出”圖標（平行四邊形），拖拽到流程線上釋放，在輸出圖標內鍵入變量S。

結果表明，這個程序框圖所對應的程序代碼是正確的，從而也表明程序框圖是正確的。

再來分析一下復雜的數學問題——考拉茲猜想。

（一）算法設計

德國數學家考拉茲（Lothar Collatz）于1930年代提出考拉茲猜想，又名3n+1猜想或冰雹猜想，是指對于每一個正整數，如果它是奇數，則對它乘3再加1；如果它是偶數，則對它除以2，如此循環，最終都能得到1。設計算法驗證考拉茲猜想（當然只能是在有限的數據范圍內驗證），還是先用自然語言來描述算法：

第1步輸入n（正整數）；

第2步若n為偶數，則將其除以2，否則（n為奇數），將其乘以3后加上1，結果仍用n表示；

第3步如果n=1，退出到第4步，否則轉回到第2步；

第4步輸出“考拉茲猜想成立！”

此時，用《畫程》軟件繪制流程圖：

第1步，拖入一個輸入圖標，在其內鍵入n；

第2步，拖入一個判斷-分支圖標，條件怎么寫？“n是偶數”，如何用計算機的語言表達呢？n除以2所得余數為0。在VB［4］或QBX7.1中用mod表示取余運算，如5 mod 3表示5除以3所得余數（為2），所以鍵入條件n mod 2=0，在“是分支”里拖入一個“處理”圖標，在“處理”圖標里鍵入賦值語句n=n2。在“否分支”里拖入一個“處理”圖標，鍵入賦值語句n=n*3+1（如圖2）。

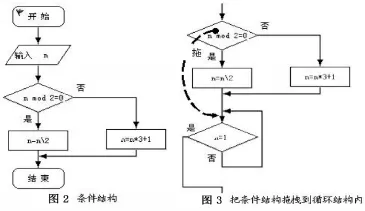
第3步，這里有一個詞非常關鍵：“轉回”！也就是說，流程線要回到上面來！要用“判斷-循環”圖標，拖入一個“判斷-循環”圖標，條件怎么寫呢？鍵入n=1，“如果n=1則退出”，所以這個“否”與“是”要交換，只要雙擊“是”或“否”就改變了（如圖3）。“否則，轉回第2步”，要轉到上面來，怎么操作呢？流程線不能拖動，可以把上面的條件結構拖拽到循環返回線的下面來（如圖3），這樣就實現了“轉回第2步”。

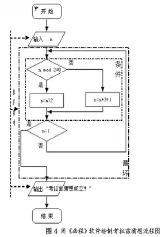
第4步，拖入一個輸出圖標，鍵入“考拉茲猜想成立！”（如圖4）

（二）三種基本結構

人們已經證明：任何復雜的程序結構，都可以用三種基本結構（順序結構、條件結構、循環結構）或它們的組合來表示。

本例的總體結構是：①輸入n；②驗算考拉茲猜想；③輸出結論。它們構成了順序結構，其中“驗算考拉茲猜想”就是循環結構（由判斷-循環圖標“n=1”主導），而“n是否偶數”組成的條件結構，嵌套于上述的循環結構的循環體內，這樣，本例同時包含了三種基本結構。

（三）單步運行

保存剛才所畫流程圖，編譯、運行程序（注意n為正整數，且任何時候n不超出2147483647）。這個程序很快就輸出“考拉茲猜想成立！”由于其中間運行過程看不到，是不是有點不放心？選擇“單步運行”功能，可以一步一步地運行程序，用戶可以“看清”每步運行的結果。單擊“單步運行”工具，彈出一個提示框，單擊“確定”按鈕，彈出“單步運行”窗體，單擊“開始”（或“下一步”）按鈕將開始單步運行（若勾選“自動”復選框，則自動單步運行（如圖5）。

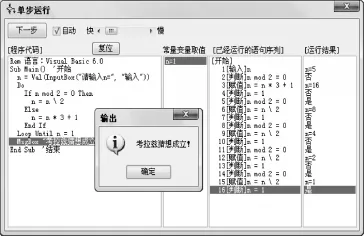
圖5“單步運行”窗體展示程序每一步運行的狀況

信息技術與高中數學算法教學整合能幫助學生從枯燥、深奧的算法理論上升到理解、消化知識的高度。信息技術為學生提供直觀、易操作讓學生所見所得的算法內函展示，使深奧的數學算法理論通過手、眼、腦等多種器官的刺激深深扎根于學生的知識體系中。

［1］數學課程標準研制組.普通高中數學課程標準（實驗稿）［S］.北京：北京師范大學出版社，2000.

［2］張景中.超級畫板自由行［M］.北京：科學出版社，2006.

［3］伍先軍.流程圖（程序框圖）高考題型例解［J］.中學數學，2012（3）.

［4］張福祥.VB程序設計基礎工業［M］.北京：中國電力出版社，2003.

（責任編輯：鄒開煌）