橫向聯(lián)系，縱向延伸
——例談數(shù)學(xué)學(xué)習(xí)中的知識(shí)點(diǎn)化和拓展

江蘇省海門市能仁中學(xué) 花永平

橫向聯(lián)系，縱向延伸
——例談數(shù)學(xué)學(xué)習(xí)中的知識(shí)點(diǎn)化和拓展

江蘇省海門市能仁中學(xué) 花永平

數(shù)學(xué)的學(xué)習(xí)不是單一、獨(dú)立的個(gè)體，從數(shù)學(xué)方面來(lái)分析，數(shù)學(xué)每個(gè)知識(shí)與技能之間都是精密聯(lián)系、融會(huì)貫通、相輔相成的。從學(xué)術(shù)上面分析，數(shù)學(xué)和其他學(xué)科之間又是相輔相成的。本文結(jié)合教學(xué)實(shí)踐，談?wù)勅绾卧诮虒W(xué)實(shí)踐中注重?cái)?shù)學(xué)學(xué)科間的聯(lián)系，達(dá)成橫向聯(lián)系，縱向延伸的效果，最終促使學(xué)生學(xué)習(xí)效率的提升，學(xué)習(xí)能力的提升。

橫向；縱向；聯(lián)系；延伸

數(shù)學(xué)學(xué)科作為一門基礎(chǔ)學(xué)科，雖然由很多微小的知識(shí)點(diǎn)構(gòu)成，但是知識(shí)點(diǎn)不是孤立的，它們之間有關(guān)聯(lián)，有類比，有拓展，有延伸。

一、教學(xué)小片段

1.人教版七年級(jí)上冊(cè)中線段中點(diǎn)定義和推理教學(xué)。

把紙條對(duì)折，找出它的中點(diǎn)。（操作層面）

若線段上的一點(diǎn)將線段平均分為兩份，這樣的點(diǎn)叫作線段的中點(diǎn)。（文字語(yǔ)言）

若M為線段AB上的點(diǎn)，且AM=BM，則點(diǎn)M為線段AB的中點(diǎn)。即因?yàn)辄c(diǎn)M是線段AB的中點(diǎn)，所以。（符號(hào)語(yǔ)言）

2.定義本質(zhì)：揭示了位置和數(shù)量關(guān)系的相互轉(zhuǎn)化。

3.基本應(yīng)用：母題：如圖1，點(diǎn)M為線段AB的中點(diǎn)，AB=8，求AM的長(zhǎng)。

教學(xué)設(shè)計(jì)：要求學(xué)生掌握一步推理：

4.變式一：如圖 2點(diǎn)C為線段AB上的任意一點(diǎn)，M為AB的中點(diǎn)，N為BC的中點(diǎn)。AB=8，求MN的長(zhǎng)。

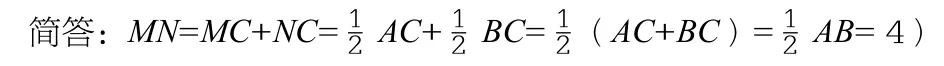
變式二：接變式一，如果點(diǎn)C為直線AB上的任意一點(diǎn)，M為AC的中點(diǎn)，N為BC中點(diǎn)。AB=8，求MN的長(zhǎng)。分類討論：點(diǎn)C在線段AB上或者在它的延長(zhǎng)線上。

①C在線段AB上，如變式一。

二、橫向聯(lián)系

與線段等價(jià)的一個(gè)幾何圖形為角，與線段中點(diǎn)對(duì)應(yīng)的是角的平分線，在數(shù)學(xué)學(xué)習(xí)中采用類化學(xué)習(xí)方式對(duì)角平分線的相關(guān)計(jì)算作出研究。……