高等數學中一元函數幾類常用極限求法實例探析

黔南民族師范學院數學系 向 彪

高等數學中一元函數幾類常用極限求法實例探析

黔南民族師范學院數學系 向 彪①

函數極限的求法是高等數學學習的難點問題之一，也是全國研究生入學考試公共數學科目必考的內容。求極限的方法較多，本文總結出了幾種常用的求極限的方法，并給出了幾道考研真題實例，希望對考研的同學有一定的幫助。

極限；洛必達法則；實例

極限貫穿高等數學始終，極限的求法是高等數學學習的難點問題之一。在實際解題過程中，函數極限的求法是多種多樣的，同學們在學習過程中，往往對求極限的方法難以選擇，不知道用哪種方法好，因此，分析和研究函數極限的求法，是非常有必要的。求極限的方法種類繁多，本文有針對性地研究討論了幾種在實際計算中用得較多、考研真題中出現較多的幾種。

一、函數極限的定義

設函數f（x）在點的某一去心鄰域內有定義。如果存在常數A，對任意給定的正數ε（無論ε它有多小），總存在正數δ，使得當x滿足時，對應的函數值都成立，則稱A為函數f（x）當x→x0時的極限，記作：恒有：。

二、函數極限求法例析

1.利用兩個重要極限求極限

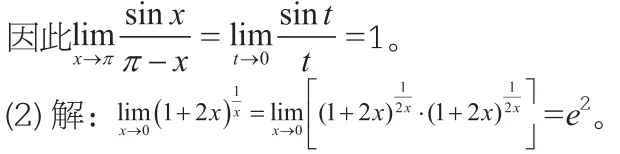
2.利用兩邊夾原理求極限

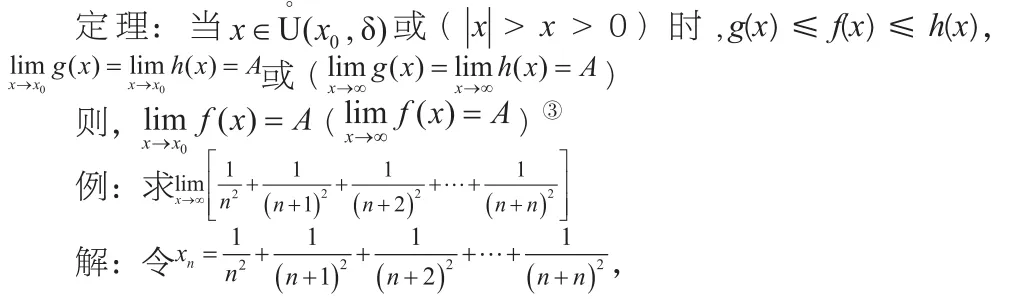
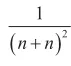
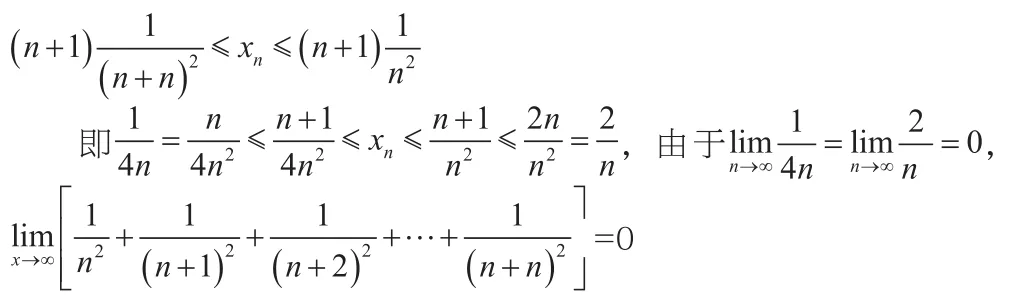
3.等價無窮小代換求極限

注意：求兩個無窮小之商的極限時，分子與分母都可用等價無窮小來代替，乘法項可直接代替，加減法項不可直接代替，加減項只能整體代換！

4.利用洛必達法則求極限

5.利用麥克勞林展開式求極限

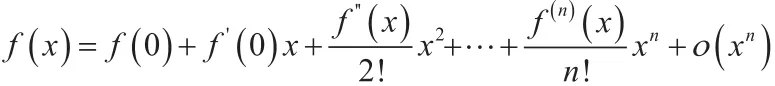
三、考研真題分析

在實際解題過程中，尤其是在研究生入學統一考試數學題目中，求極限絕不會局限于使用某一種方法，都是幾種方法結合在一起使用的，靈活度較高，這就要求我們在具體的解題過程中思維開闊，不鉆死胡同，靈活運用，下面舉幾個考研的例題來說明。

（此步驟，使用了等價無窮小替換方法，學生必須牢記常用的幾種等價無窮小，才能熟練使用這一方法。）

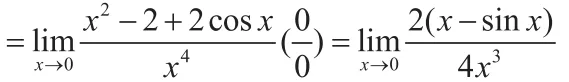
（此步驟，使用羅比達法則）

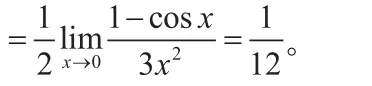
［1］同濟大學數學系.高等數學（上下冊，第七版）［M］.北京：高等教育出版社，2014.

［2］華東師范大學數學系.數學分析［M］.北京：高等教育出版社，2001.

［3］陳文燈.數學復習指南［M］.北京：世界圖書出版社，2014.

①向彪（1982-），男，貴州江口人，碩士，黔南民族師范學院講師，研究方向：基礎數學。

②同濟大學數學系.高等數學（上冊，第七版）19頁

③同濟大學數學系.高等數學（上冊，第七版）27頁

④同濟大學數學系.高等數學（上下冊，第七版）187頁