習題課教學:從“拿來主義”走向編題變式——以“數軸再認識”習題課為例
☉江蘇省海安縣胡集初級中學 王秀梅
習題課教學:從“拿來主義”走向編題變式——以“數軸再認識”習題課為例
☉江蘇省海安縣胡集初級中學王秀梅
不少數學教育學者(如人民教育出版社中數室章建躍編審)指出:要重視數學核心概念的教學.而對于所謂“核心概念”的界定又顯困難,通常需要教師根據自身對數學的理解、對學生的理解、對教學的理解來確定哪些概念是“核心概念”,需要并值得在教學中增設課時進行重視和強化.比如,筆者認為,學生剛進入初中,數系剛擴充到有理數,就引出數軸的概念,基于數軸定義了相反數、絕對值等重要概念,為后續研究有理數的運算提供了奠基作用,則數軸可看成是有理數基礎概念中的核心概念.根據以上認識,我們在教材內容之外,在數軸、相反數、絕對值教學之后,自主增設了數軸習題課,引導學生對數軸再認識,起到了較好的教學效果.本文整理該課的教學設計,并跟進教后反思,供研討.
一、數軸習題課教學設計
教學環節(一):從數軸出發
(1)數軸的概念;簡要回顧從溫度計(如圖1)抽象出數軸(如圖2),安排學生回顧數軸的三要素(原點、正方向、單位長度).

圖1

圖2
(2)數軸與相反數的關系.
在數軸上,到原點距離相等的點有兩個,這兩個點所表示的數符號相反,稱它們為相反數.
(3)數軸與絕對值的關系.
在數軸上,表示數a的點與原點的距離叫作數a的絕對值.
(4)數軸與數的大小比較.
數學中規定,在數軸上表示有理數,它們從左到右的順序,就是從小到大的順序,即左邊的數小于右邊的數.
(5)數軸與有理數的運算.
比如,即將要學習的有理數加法運算中的異號兩數相加,本質上是將互為相反數的部分抵消.可舉例示范:-3+2=-1+(-2)+2=-1.
設計意圖:數軸是進入初中第一個數形結合的工具,不僅可以把有理數表示對應到數軸上,而且是后續定義相反數、絕對值的基礎,又是研究數的運算的一種工具,還是以后學習平面直角坐標系的基礎.
教學環節(二):典例分析
例1如圖3,數軸上,點A、B分別表示a、b.

圖3
(1)從圖中讀出a=______,b=______;
(2)在圖中標出a的相反數-a;
(3)點B到原點的距離是多少?
(4)點A、B之間的距離是多少?
(5)將點B向右移動7個單位到達點C,則點C到點A的距離是多少?
【預設講評】
(1)a=2,b=-3;
(2)在-2處標出即可,圖略;
(3)3;
(4)5;
(5)點C對應著數4,則點C到點A的距離是2.例2如圖4,數軸上,點A、B分別表示a、b.

圖4
(1)從點B所在位置來看,數b是一個正數還是負數呢?
(2)在數軸上標出表示-b的數,并用點B′表示;
(3)比較a、b、-a、-b的大小,用“<”連接;
*挑戰*(4)設線段AB的中點為M,點M對應的數是m,試用含a、b的式子表示m.
【預設講評】
(1)b是負數;
(2)在原點右側,與點B等距離的位置標出點B′,圖略;
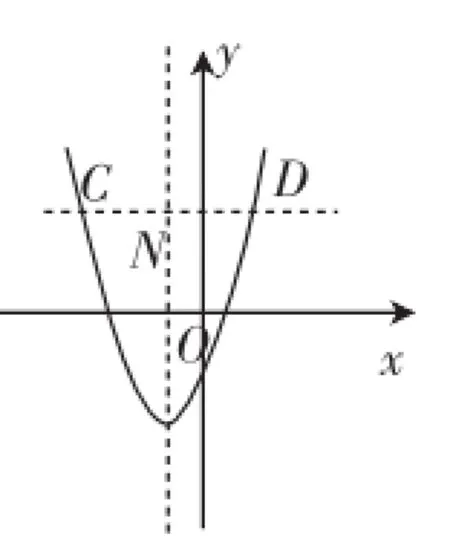
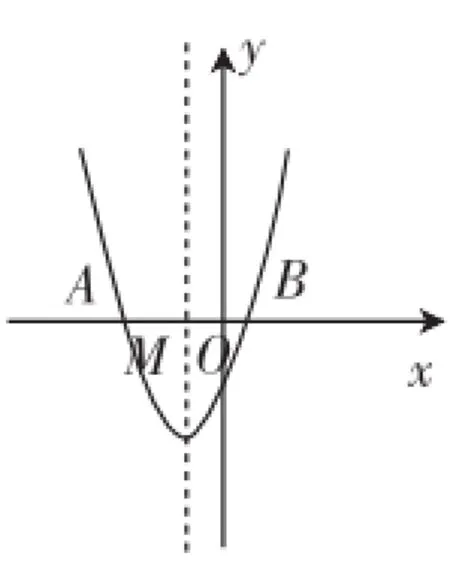
(3)在圖中再標出表示-a的點,這樣可以由數軸上數的大小關系,直接寫出b<-a (4)可以從特殊值出發,比如取a=2,b=-3時,m=-0.5;a=1,b=-4時,m=-1.5;a=3,b=-1時,m=1;…;可歸納出m= 教學環節(三):變式訓練,聽課檢測 變式題:如圖5,點M、N是數軸上兩點,對應著數m、n. 圖5 (1)當m=-3,n=2.9時,M、N之間的距離,即MN= _____; (2)將點N向左移動5個單位后對應著點A,若點A還在M點右邊一個單位,則MN=________; *挑戰*(4)若點A對應著1,當MA=NA時,求4m+4n+ 2008的值. 【預設解答】 (1)5.9; (4)結合上面例題中所探究的中點與線段兩端點對應數之間的關系,可以發現m+n=2,則4m+4n+2008的值為4×2+2008=2016. 設計說明:針對前面的例題的類型進行的變式訓練,前三問屬于簡單變換字母、數字,而最后一問則是對上面例題中的最后一問的變式拓展,需要學生有整體求解的策略.這里也可順便鏈接九年級二次函數的一類習題,如圖6,二次函數y=ax2+bx+c的圖像(拋物線)與x軸交于點A(x1,0)、B(x2,0),拋物線的對稱軸與x軸交于點M(m,0),一定有(x1+x2).二次函數學習時,不少學生不能靈活運用該性質處理有關問題,如圖7,當問題變式到直線y=e與拋物線相交于C(x3,e)、D(x4,e),時,與對稱軸交于N(n,e),仍然有.對比例2(4)、變式題(4),就會發現,雖然較難,但是它們都“指向將來”,讓學生提前熟悉這類問題或結構是十分有益的. 圖7 圖6 1.習題課的增設需要專業自主,是“用教材教”的體現 通常情況下,較為重要的數學概念或性質教學之后,都會安排習題課,但習題課的內容卻是訂正學生手頭的所謂教輔資料上的相關習題,成為習題訂正或講評課.我們所謂的增設習題課是指教師在新授課期間主動預設的一種課型,需要基于專業自主,組織教學內容,增設出來的習題課.這也是教師從“教教材”走向“用教材教”(鐘啟泉教授語)的一種專業追求. 2.習題課的開課階段需要梳理回顧,復習相關概念或性質 習題課的開課階段需要梳理近階段相關概念的關系,如上面數軸的習題課開課時,我們把與數軸相關的一些概念、性質、應用都梳理一遍,促進學生自主建構、形成知識網絡、完善知識體系,讓學過的知識能像葡萄一樣串起來,即所謂“串珠成線”.比如從數軸出發,我們定義了相反數,基于這個平臺又定義了絕對值,并且可以比較有理數的大小,還可以利用數軸研究符號不同的兩個有理數的大小,等等.直到以后引入平面直角坐標系時,從“一維”的數軸到“二維”的平面直角坐標系,根據教學經驗,如果學生對數軸上的點與數的對應理解得較為深刻,則過渡到平面直角坐標系時,往往也會有較好的適應性. 3.習題課的例題選擇忌簡單拿來主義,倡導精心編擬,變式拓展 聽過不少習題課的隨堂課,特別是跟隨校領導“聽隨堂課”時,有些教師的作業訂正課就是一種習題課,被聽課者往往也自知“今天講練習冊,沒什么好聽的”.然而如果習題課上的例題不是簡單的拿來主義,而是經過教師精心預設或原創編擬,并經過系列變式拓展,那么習題課也會有很精彩的表現.在精心編擬習題課上的例、習題時,我們有如下一些建議:首先是習題的類型不能超過課標、教材上的典型問題,而是在教材習題的基礎上適當變式;接著可以先由簡單的改編數字、字母出發,再變換設問方式,最后拓展生長,讓高層次學生接受挑戰. 4.習題課的“后半段”需要開展變式檢測,反饋聽課效果 習題課的教學要保證必要的練習量,除了在例題講評環節注意讓學生保持思維參與、積極運算,一個重要的教學環節就是留出10分鐘左右對前面講評環節中的例題開展變式再練.這個教學建議得益于《中學數學》(下)上相關文章中的教學建議,筆者認為,重視聽課檢測是十分重要的,因為學生“聽懂”并不一定“會做”,特別是中下層次的學生往往誤認為自己聽懂就會了,其實只要稍作變式,他們還是顯得很吃力.當然,預設聽課檢測時,也應注意保持高層次學生的積極性,這就是如上面聽課檢測環節那樣,在最后一問設計一道挑戰題,可以讓高層次學生也不能在規定時間順利挑戰成功,這一方面可以促進他們深入思考、長時間思考,另一方面也是追求“這節課可以下課,但思考并不一定就停止”的教學理念. 習題課是一種經典課型,特別是在當下應試教學盛行的時代,如何讓習題課上出新意、上出創意,是值得我們深入研究的課題,本文拋磚引玉,期待批判和更多的課例跟進. 1.付小飛.明辨并列與遞進,引導分離和聚焦——2016年江蘇蘇州中考第28題解析與教學思考[J].中學數學(下),2016(7). 2.周紅娟.開放與放開:概念生成與例題變式的教學追求——從“三角形內角和”教學說起[J].中學數學(下),2016(8). 3.鄭毓信.“開放的數學教學”新探[J].中學數學月刊,2007(7). 4.鄭毓信.善于舉例[J].人民教育,2008(18). 5.鄭毓信.善于提問[J].人民教育,2008(19). 6.鄭毓信.善于優化[J].人民教育,2008(20).Z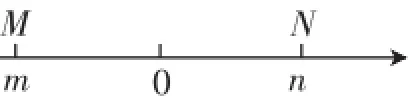
二、關于“習題課”的相關思考
三、結束語

