從概念理解的角度審視圖形的變換教學

☉江蘇省無錫市金星中學　潘小娟

從概念理解的角度審視圖形的變換教學

☉江蘇省無錫市金星中學潘小娟

數學概念教學，目的是讓學生領會數學內在的思想方法，使學生從中掌握關于數學思想方法方面的相關知識，并使這些知識逐步內化成為自身學習體系的一部分.對于初中幾何而言，圖形變換問題是繞不開的一個重要知識點，學生只有掌握好了相應的知識，才能在幾何學習中進退自如、游刃有余.作為對全等變換的深入理解和有效實踐，下面就從概念理解的角度，詮釋一下筆者是如何進行這樣的理解與把握的.

一、關聯概念，關注知識內容的聯系

在知識的內部，始終呈現出一種結構化的特點.在教學中，教師應當把握好這樣的特點，把握好知識點之間的內在關聯，下面先來看這樣的一個實例：

問題1：如圖1，在Rt△AOB中，兩直角邊OA、OB分別在x軸的負半軸和y軸的正半軸上，將△AOB繞點B逆時針旋轉90°后得到△A′O′B.若反比例函數的圖像恰好經過斜邊A′B的中點C，S△ABO=4，tan∠BAO=2，求k的值.

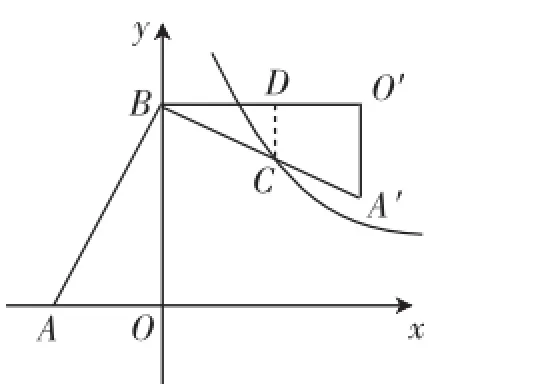
圖1　

分析：先根據S△ABO=4，tan∠BAO=2，求出AO、BO的長度，再根據C為斜邊A′B的中點，求出點C的坐標，點C的橫縱坐標之積即為k值.

解：設點C坐標為（x，y），作CD⊥BO′交邊BO′于點D，因為tan∠BAO=2，所以因為S所以AO=2，BO=4.因為△ABO≌△A′O′B，所以AO=A′O′=2，BO=BO′=4.因為C為斜邊A′B的中點，CD⊥BO′，所以所以x=BO-CD=4-1=3，y= BD=2，所以k=x·y=3·2=6.

這一問題從本質上來看是圖形的全等變換，背景借助了反比例函數的幾何性質，通過基本的旋轉變化來完成，可以說是課堂教學中一個不錯的研究實例.下面不妨再來從一個純概念類問題進行剖析：

概念變式：下面四個手機應用圖標（圖2）中是軸對稱圖形的是（）.

圖2　

分析：這一變式可以通過軸對稱圖形與中心對稱圖形的性質對各選項進行逐一分析，A圖是微信圖標，它既不是軸對稱圖形，也不是中心對稱圖形；選項B是中心對稱圖形；C圖既不是中心對稱圖形，也不是軸對稱圖形；D是軸對稱圖形.通過一組概念辨析，很容易就可以得到正確的結果.

從客觀上來說，教材內容及教師的教學過程都是由淺入深、循序漸進的，任何新知識的學習過程都是伴隨著原有知識的學習過程逐漸深化和拓展的.因此，教師需要不斷思考的是，如何將新知識與原有學習的舊知識聯系起來，推陳出新，以期收到良好的效果.

二、把握節奏，加深知識方法的理解

在實際教學中，教師往往希望學生的認識一開始就能定格在正確、合理的格局上.殊不知，學生對知識的理解是一個循序漸進的過程，需要經歷不斷的升華和理解，才能做到逐步領悟與提高.如果忽視學生的這一認識規律，在教學中很容易造成種種失“度”的現象發生，這樣對于學生知識的掌握和提升顯然是不利的.

問題2：如圖3，把一張矩形紙片ABCD沿EF折疊后，點A落在CD邊上的點A′處，點B落在點B′處，若∠2=40°，則圖中∠1的度數為（）.

A.115°B.120°C.130°D.140°

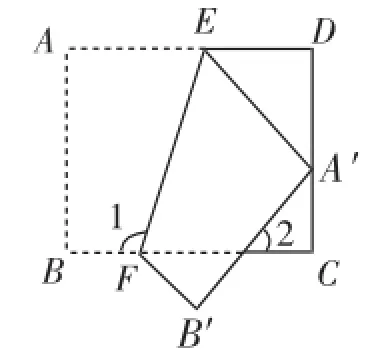
圖3　

分析：根據折疊的性質和矩形的性質得出∠BFE=∠EFB′，∠B′=∠B=90°，根據三角形內角和定理求出∠CFB′=50°，進而解答即可.

解：把一張矩形紙片ABCD沿EF折疊后，點A落在CD邊上的點A′處，點B落在點B′處，所以∠BFE=∠EFB′，∠B′=∠B=90°.因為∠2=40°，所以∠CFB′=50°，所以∠1+∠EFB′-∠CFB′=180°，即∠1+∠1-50°=180°，所以∠1=115°.

學生在學習過程中，對于翻折類問題的本質的把握往往是不到位的，尤其是在考查角度問題的時候，更容易引起中等學生的恐慌.那么，教師應當如何幫助學生度過難關呢？節奏的有效把握是關鍵，對方法的理解是重點.問題2中，對應角的尋找無疑是一個關鍵之處，把握翻折前后對應角相等也成為解決此類問題的核心.教師在教學中，不妨注意問題的方法的反復鞏固，可以適當地進行一組變式問題的再練習，提升方法的熟練度和掌握程度.

變式1：如圖4，Rt△AOB中，∠AOB=90°，OA在x軸上，OB在y軸上，點A，B的坐標分別為把Rt△AOB沿著AB對折得到Rt△AO′B，則點O′的坐標為_________.

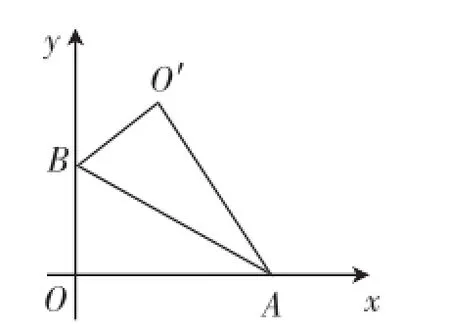
圖4　

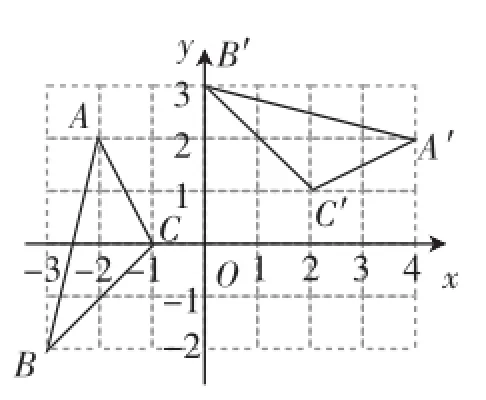
圖5　

變式2：如圖5，在平面直角坐標系xOy中，△A′B′C′由△ABC繞點P旋轉得到，則點P的坐標為_______.分析：從翻折到旋轉的變化，本質是不變的.

圖6　

分析：扇形面積的計算，用到的也是圖形旋轉的不變性.

三、注重感悟，構建整體內容的脈絡

人教社章建躍博士說過：“教之道在于度，學之道在于悟.”對于具體概念而言，有時候學生會局限在自己原有的生活經驗之中，在認識水平上存在一定的局限，學生的問題往往就會在領悟方面存在誤區.此時，教師更應該把握好教學的度，幫助學生處理好常見的易錯點和難點，實現教學中的飛躍.

問題3：將拋物線y=-x2先向下平移2個單位，再向右平移3個單位后所得拋物線的解析式為________.

解析：拋物線y=-x2先向下平移2個點位，再向右平移3個單位后所得拋物線的解析式為y=-（x-3）2-2，化簡得y=-x2+6x-11.

變式1：將點A（1，-3）沿x軸向左平移3個單位長度，再沿y軸向上平移5個單位長度后得到的點A′的坐標為________.

解析：點A（1，-3）沿x軸向左平移3個單位長度，再沿y軸向上平移5個單位長度后得到點A′，所以點A′的橫坐標為1-3=-2，縱坐標為-3+5=2，所以A′的坐標為（-2，2）.故答案為：（-2，2）.

變式2：如圖7，一段拋物線：y=-x（x-2）（0≤x≤2）記為C1，它與x軸交于兩點O，A1；將C1繞A1旋轉180°得到C2，交x軸于A2；將C2繞A2旋轉180°得到C3，交x軸于A3；…如此進行下去，直至得到C6，若點P（11，m）在第6段拋物線C6上，則m=_______.

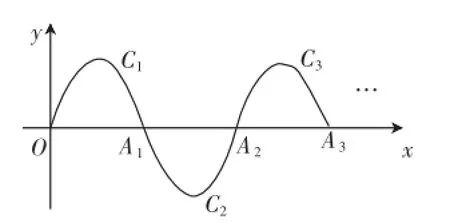
圖7　

四、挖掘深化，不斷拓展數學思維

從教學過程到教學形式，教師都需要進行細致把握，無論是模式識別、方法調整到最后的反思小結，都是一個自然的教學過程的，教師在其中應當把這種合情合理的、符合思維規律的解決問題的方法分析給學生，讓學生能夠真正地領悟與思考，從思考中有所悟，有所得.

圖形的變換，本質在于圖形結構的不變性，幾何性質的穩定性，而對于解題的教學也應該把握這一“根本”，在理解概念的前提下，靈活地進行教學與研究.

問題4：如圖8，方格中，每個小正方形的邊長都是單位1，△ABC在平面直角坐標系中的位置如圖.（1）畫出將△ABC向右平移2個單位得到的△A1B1C1；（2）畫出將△ABC繞點O順時針方向旋轉90°得到的△A2B2C2；（3）求△A1B1C1與△A2B2C2重合部分的面積.

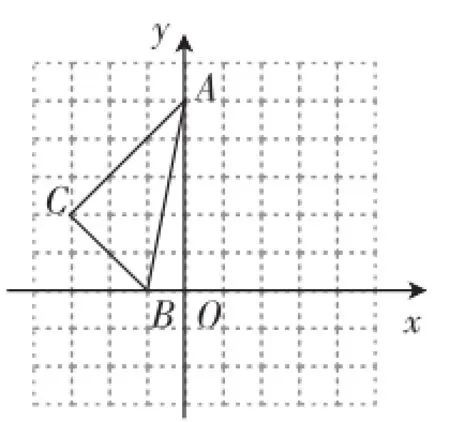
圖8　

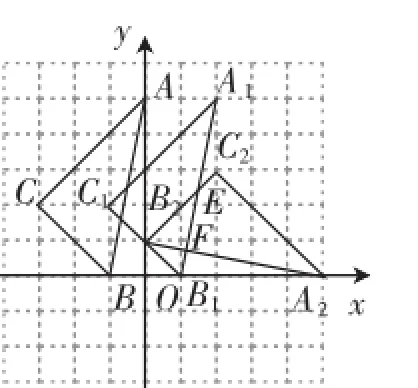
圖9　

解析：（1）、（2）作圖，如圖9所示；下面具體來剖析一下（3）的解答過程，B2C2與A1B1相交于點E，B2A2與A1B1相交于點F，如圖9，因為B2（0，1），C2（2，3），B1（1，0），A1（2，5），A2（5，0），所以直線A2B2為y=5x-5，直線B2C2為 y=x+1，直線A2B2為由解得以點由解得所以點所以故△A1B1C1與△A2B2C2重合部分的面積為

五、一點感悟

對概念的精準理解和把握是理解圖形變換的前提和基礎，充分展示解題過程中的思維生長過程是重要的核心.在解決圖形變換類問題時，教師除需要教給學生簡潔的方法之外，也應該通過一組變式的形式將整個思維過程呈現在學生的眼前，讓學生做到觸類旁通，舉一反三，真正實現“解一題、會一類、通一片”的效果.