理解綜合題立意，預設教學微設計——以2016年江蘇宿遷卷第26題為例

☉江蘇省南通市通州灣三余中學　施　勤

理解綜合題立意，預設教學微設計——以2016年江蘇宿遷卷第26題為例

☉江蘇省南通市通州灣三余中學施勤

近讀《中學數學》（下），發現很多中考壓軸題的研究文章都能從解題探討走向“一題一課”、“教學微設計”等教學思考的方向，這些接地氣的文章使對解題教學十分有益，只要稍加利用，制作成課件，就可直接拿到初三復習課、習題課上去教學使用，受此啟發，筆者也對一道壓軸題開展了教學微設計，并在校內教研課中成功展示，得到同事的好評.本文就是呈現該題的思路及微設計，提供研討.

一、考題及思路突破

考題（2016年江蘇宿遷中考卷第26題）如圖1，在平面直角坐標系xOy中，將二次函數y=x2-1的圖像M沿x軸翻折，把所得到的圖像向右平移2個單位長度后再向上平移8個單位長度，得到二次函數圖像N.

（1）求N的函數表達式；

（2）設點P（m，n）是以點C（1，4）為圓心、1為半徑的圓上一動點，二次函數的圖像M與x軸相交于兩點A、B，求PA2+PB2的最大值；

（3）若一個點的橫坐標與縱坐標均為整數，則該點稱為整點.求M與N所圍成封閉圖形內（包括邊界）整點的個數.

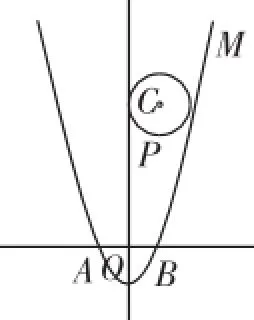
圖1　

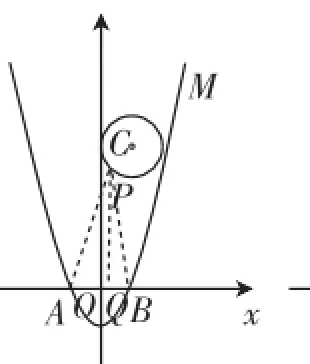
圖2　

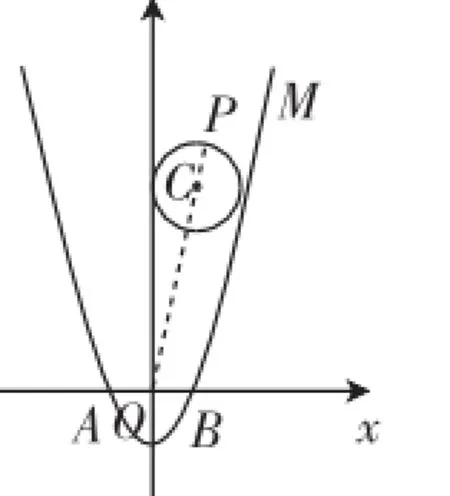
圖3　

1.思路突破

（1）先由關于x軸翻折的拋物線解析式變化規律，得翻折后的拋物線的解析式是y=-x2+1，根據拋物線平移規律，容易分析出平移后的拋物線解析式為y=-（x-2）2+ 9，即y=-x2+4x+5.

（2）設問中的PA2+PB2容易想到構造直角三角形，利用勾股定理列式，如圖2，連接PA，PB，作PQ⊥AB于點Q，在Rt△PAQ中思考，PA2=（m+1）2+n2.同理在Rt△PBQ中思考，PB2=（1-m）2+n2；于是PA2+PB2=（m+1）2+n2+（1-m）2+ n2，整理得PA2+PB2=2（m2+n2）+2，至此，有一個重要的進展就是OP2=m2+n2，也就是PA2+PB2=2OP2+2.接著的難點就是當OP取得最大值時，PA2+PB2就取得最大值，進而構造圖3，當點P位于OC延長線上時，此時OP取得取大值.接著利用OP=OC+PO可計算得所以PA2+PB2的最大值為（3）這一問可以構造相對精準的草圖分析，如圖4.

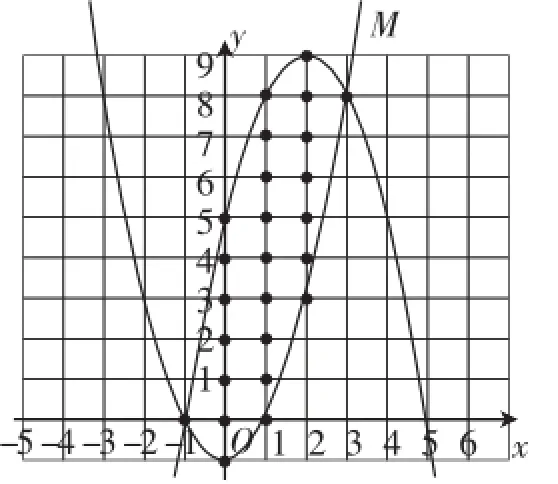
圖4　

需要畫準圖形的幾個地方，第一，兩條拋物線的交點分別是（-1，0），（3，8），這兩個交點也是符合要求的；第二，思考當x=0時符合要求的整數點有7個，當x=1時符合要求的整數點有9個，當x=2時符合要求的整數點有7個，M與N所圍成封閉圖形內（包括邊界）整點的個數為1+7+9+7+1=25個.

2.解后反思

這道考題的第（2）問有一定的難點，且與前后問題之間缺少必要的關聯，根據筆者教學經驗，第（2）問要難于第（3）問，因為后者只要精準作圖輔之計算驗證就可獲得解答，對思維的要求并不太高；而第（2）問的主要障礙有如下幾點：

難點1：用含m，n的式子表示PA，PB的平方和.

通常都想方設法用一個參數來表示PA，PB的平方和，但對于此題來說，此路難通，即使把高中階段的圓的解析式（即（m-1）2+（n-4）2=1）利用起來，也難以將PA，PB的平方和用一個參數來表示.

難點2：想到OP2=m2+n2.

當PA，PB的平方和被表示為2（m2+n2）+2后，要及時聯系到OP2，這樣對于問題獲得轉化有很大的幫助，是該題的重要進展之一.

難點3：想到點P在OC延長線上.

當問題進展OP最大時，PA，PB的平方和最大時，及時構造出圖3進行分析.

二、教學微設計

1.開課階段

例1如圖1，在平面直角坐標系xOy中，將拋物線C1：y=x2-1沿x軸翻折后，再向右平移2個單位長度，繼續向上平移8個單位長度，得到拋物線C2.

（1）請指出最后得到的拋物線C2的解析式；

（2）寫出拋物線C2的頂點坐標；

（3）求拋物線C2與坐標軸的交點坐標；

（4）設直線x=1與拋物線C1，C2分別交于M，N兩點，求線段MN的長.

設計意圖：將翻折、平移變換前后的兩條拋物線組合起來進行探究，并引導學生辨析拋物線C2與坐標軸的交點，以及直線x=1時求MN的長，對應著原考題的第（3）問.

2.考題探究

例2如圖1，平面直角坐標系xOy中，拋物線y=-x2+ 1交x軸于A，B兩點.以點C（1，4）為圓心的⊙C與y軸相切.設點P（m，n）為⊙C上一點.

（1）連接OP，用含m，n的式子表示OP2；

（2）連接PA，分析線段PA的最值（包括最大值和最小值）；

（3）設d=PA2+PB2，用含m，n的式子表示d；

（4）在（3）的條件下，分析d的最值（包括最大值和最小值）.

設計意圖：這個考題對應原考題的第（2）問，通過增設系列輔助追問，使得難點得到分解和鋪墊.而且將原考題中分析d的最大值拓展到分析它的最大值與最小值.

3.拓展思考

例3題干同例2.

（1）當m=1時，求點P的坐標；

（2）當m=2時，若直線PC與拋物線交于D點，求點D的坐標；

（3）若拋物線上有一點Q，連接PC，PQ.

①求PC的最小值；

②求PQ的最小值.

設計意圖：受到文2的啟發，增設了定點到拋物線上動點到定點的距離探究.使得問題走向拓展，提供高層次學生向上挑戰.

4.變式再練

變式再練：如圖5，在平面直角坐標系xOy中，將拋物線C1：y=x2-4沿x軸翻折后，再向右平移2個單位長度，繼續向上平移9個單位長度，得到拋物線C2.

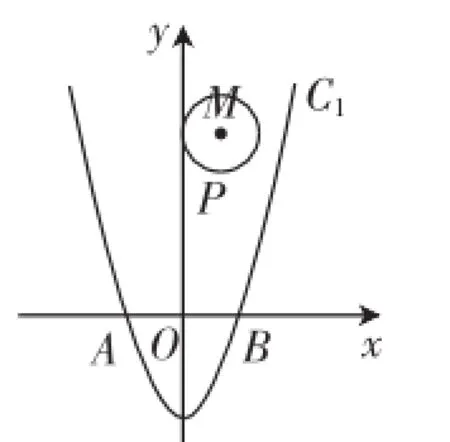
圖5　

（1）直接寫出拋物線C1與x軸的交點A，B的坐標.

（2）直接寫出拋物線C2與坐標軸的交點坐標.

（3）以點M（1，4）為圓心的⊙M與y軸相切.設點P（m，n）為⊙M上一點.

①用含m，n的式子表示PA2+PB2的長；

②分析PA2+PB2的最值（含最大值與最小值）.

（4）若一個點的橫坐標與縱坐標均為整數，則該點稱為整點.求拋物線C1與C2所圍成封閉圖形內（包括邊界）整點的個數.

設計意圖：首先是對題干上的拋物線解析式的數據、圖像上的字母都做了改編，接著是后續系列設問涵蓋了前面教學環節中訓練到的一些考點.特別是第（3）問關于最大值、最小值的拓展思考，包括第（4）問在變換數據之后，仍然探討整點問題，都可看成是對原考題的豐富和生長.

三、寫在最后

習題課教學到了初三中考復習時，往往是中考題匯編起來的解題教學，一節課中選題常常是“形似”，難有“神似”.想來，針對一道綜合題而設計的“一題一課”常常能從“形似”走向“神似”，也是解題教學從繁雜走向簡約的一種追求.期待更多的課例跟進，研討和豐富這個課題方向.

1.鄭毓信.多元表征與概念教學［J］.小學數學教育，2011（10）.

2.蔣建東.一道“階段考題”的思路突破與講評設計［J］.中學數學（下），2016（5）.