藏鋒內斂：例說綜合題命制中的分類討論——由2016年山西省壓軸題的拓展思考說起

☉江蘇省鹽城市大豐區實驗初中　楊劍峰

藏鋒內斂：例說綜合題命制中的分類討論——由2016年山西省壓軸題的拓展思考說起

☉江蘇省鹽城市大豐區實驗初中楊劍峰

中考綜合題特別是壓軸題常常會考查分類思想，以便檢測學生數學思維的嚴謹性、慎密性.也有些考題對分類討論提出過高要求，陷入失控、無度狀態.本文先對一道考題的第（3）問進行思路解析，并拓展思考，最后圍繞綜合題命制中對分類討論的調控提出一些初步思考，提供研討.

一、考題的思路突破

圖1　

考題（2016年山西省第23題）如圖1，在平面直角坐標系中，已知拋物線y=ax2+bx-8與x軸交于A，B兩點，與y軸交于點C，直線l經過原點O，與拋物線的一個交點為D，與拋物線的對稱軸交于點E，連接CE，已知點A，D的坐標分別為（-2，0），（6，-8）.

（1）略；（2）略；

（3）若P是y軸負半軸上的一個動點，設其坐標為（0，m），直線PB與直線l交于點Q，試探究：當m為何值時，△OPQ是等腰三角形.

以下重點展開第（3）問思路突破：首先要分析待求的△OPQ是等腰三角形有幾種不同情形，考慮到點P是y軸負半軸上一個動點，且△OPQ頂點Q是由直線PB與直線l相交所得，故不可能有OP=PQ.只可能存在兩種情況，即OP=OQ或OQ=PQ.以下構造出草圖（如圖2，圖3）.

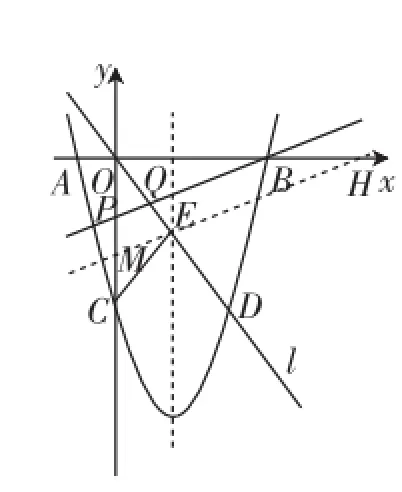
圖2　

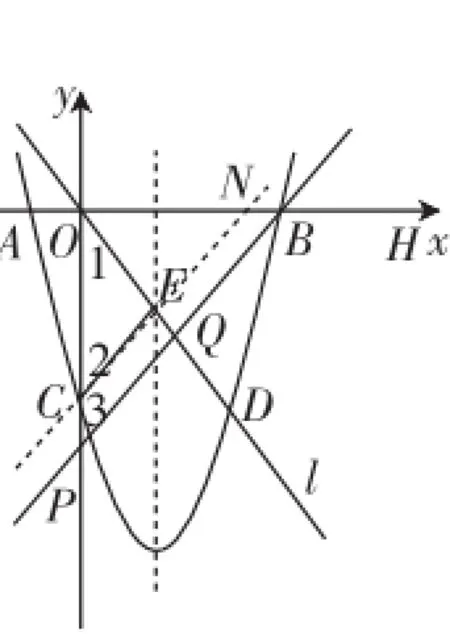
圖3　

以下分述之：

①如圖2，當OP=OQ時，△OPQ是等腰三角形.此時，過點E作EM∥PQ交y軸于點M，容易得到△OME也是等腰三角形，OM=OE=5，于是可求出直線ME的解析式為y=根據兩直線平行，斜率k相等，可設直線PQ的解析式為把B（8，0）代入即可得即點此外也可考慮利用△OPQ～△OME得到的比例式，以及由MH∥PB可得，組合溝通得出答案.

②如圖4，當PQ=OQ時，△OPQ是等腰三角形.結合點E，C坐標的特征，發現△OCE是等腰三角形，OE=CE，于是可以確認CE∥PQ.可先解出直線CE的解析式為，進一步設直線PQ的解析式為把B（8，0）代入解析式可得即

二、拓展思考

考慮到第（3）問限制了點P在y軸的負半軸上，如果該點放開到y軸上任意一點，那么還會有怎樣的可能情形呢？

問題表述如下：若P是y軸上的一個動點，設其坐標為（0，m），直線PB與直線l交于點Q，試探究：當m為何值時，△OPQ是等腰三角形.

圖4　

圖5　

圖6　

先研究圖4的情形，此時OP=PQ，△OPQ為等腰三角形，可得△OPQ～△OEC，結合OE=CE=5，OC=8，有OP∶OQ=5∶8，可設OP=5m，OQ=8m，設法將Q點的坐標用含m的式子表示，如圖6，在Rt△OQH中，該三角形的三邊之比是“3∶4∶5”，可以表示出即點Q的坐標由于另有P（0，5m），B（8，0），三點都是共線的，所以就轉化為以下問題：

解析：設該直線解析式為y=kx+b，把三個點坐標分別代入直線解析式可確定出

接著研究第4種情形，如圖5，此時OP=OQ，點P在y軸正半軸，而點Q在x軸下方，可設P（0，5n），則OQ=5n，根據點Q在直線上，可得Q（3n，-4n），于是三點（0，5n），（3n，-4n），（8，0）在同一直線上，可以確定

三、命題感悟

即點P（0，24）.

從以上解法探討和拓展思考來看，山西省中考數學命題組應該已預見到如果將點P放開在y軸上深入探究，則學生在考場上限時獨立解答完整的可能性是很小的，基于內斂藏鋒的命題取向，命題組將探究的范圍適當縮小，使得問題分類討論的情形只有兩種，減小了求解的難點，值得點贊.以下再圍繞命題中分類討論的話題給出幾點進一步的思考.

1.分類討論的命題立意需要指向概念教學

初中階段的分類討論非常豐富，具體來說，代數領域由于數的范圍之豐富需要分類討論，比如實數系分有理數與無理數，或者是正數與負數，對應到一個點所在數軸上的位置，就需要分該點在數軸上的正半軸、負半軸或原點等位置，上述考題第（3）問限制了在y軸負半軸上思考，而一旦放開，則需要考慮另外的點P在y軸正半軸的兩種可能情形.再比如在幾何領域，圖形之間的不同位置關系往往會帶來分類討論，三角形全等（相似）的不同對應關系會帶來分類討論等，如本題中等腰三角形的腰沒有明確，則也會面臨著分類討論.這些分類討論的命題立意，背后都指向重視概念教學.

2.分類討論需要深思，以防陷入無度失控

分類討論是每份中考試題都會反復考查的一種重要思想方法，對于檢測學生思維嚴謹性、慎密性有著十分重要的考查功能.但是分類討類的考題也需要注意把控和反復推敲，防止失控與無度.我們常常見到有些地區的考題，一道綜合題的分類討論結論多達4種以上，有些分類討論之后運算還十分繁雜，且運算的類型也高度趨同，使得考生思路易見，運算難見終點.

3.分類討論的問題需要考慮多種解法兼容

得到普遍認可的是，中考綜合題的解法需要多樣化，因為中考面向的是大樣本甚至全樣本環境下的測試考查，一道把關題的設計高度，需要兼顧不同思維風格學生的思維特點.故命題時對于綜合題的不同分類情況，不僅要考慮分類的合理與思路如何生成，還要構思或預設學生可能的解答路徑，使得考題的內容效度與信度達到較高水平，也是試題命制中“兼顧公正”的一種追求.

四、結束語

命題也是一門遺憾的藝術，需要打磨與優化.以上我們從一道考題的思路出發，拓展思考，并基于分類討論這一思想方法在綜合題中的命題技術展開了一些初步的思考，拋磚引玉，供批評指正.

1.羅增儒.數學解題學引論［M］.西安：陜西師范大學出版社，2008.

2.鄭毓信.善于提問［J］.人民教育，2008（19）.

3.劉東升.以本為本：習題變式的視角與可能［J］.中小學數學，2016（1）.

4.鮑建生，顧泠沅，等.變式教學研究［J］.數學教學，2003（1，2，3）.