以“情”促“智”，踐行智慧再生長的數學課堂

周松

[摘 要] 學校教育行為的開展不僅僅是為了學生的升學和應試，更是為了學生的智力生長，促使學生在成長過程中的智慧再生長. 初中數學是學校課程的必修課程之一，也是決定學生升學與發(fā)展的一個必考課程，介于它的身份和地位，如何實現數學課堂中學生智慧的再生長是教學行為中必須思考和重視的一個必要環(huán)節(jié).

[關鍵詞] 方法；活動；智慧；啟發(fā)；平行線

學生的智慧再生長是學生的基于已有的知識與素養(yǎng)下建構和完善的新知識與技能體系，這些新知識與技能的建構過程中所積累的思想與方法、體驗與感受、經驗與教訓都將促使學生的智力再生長，而在智力再生長的過程中，教師如果善于引導學生將問題和方法進行分類與對比，歸類與總結，那么久而久之，這種發(fā)現問題、解決問題的能力就能得到有效的訓練和提升，學生的智慧也就順其自然地得到了再生長. 筆者在本文中就人教版“平行線”這一課談談自己如何通過以“情”促“智”的策略來促使學生在課堂學習過程中的智慧再生長.

方法初點撥，智慧先開門

學生進入初中數學的學習就已經積累了一定思想與方法，很多思想和方法都能非常有效地促使學生智力再生長. 在教學的過程中，我們一方面要在教學行為中給學生滲透新的思想與方法，并教會學生學會使用相應的思想與方法去解決相應的問題，還需要引導學生學會對已經掌握或者已經使用過的思想與方法進行不定時的總結與回顧、分析與對比，讓學生嘗試憑借自己的能力與需要進行一定的應用與提升.

而在平行線的教學過程中，我們需要引領學生在此學會使用“類比法”進行再學習和再應用，于是，筆者結合學生的學習能力采用以下方法來對“類比法”進行無聲的點撥.

自主學習，獨立思維鞏固

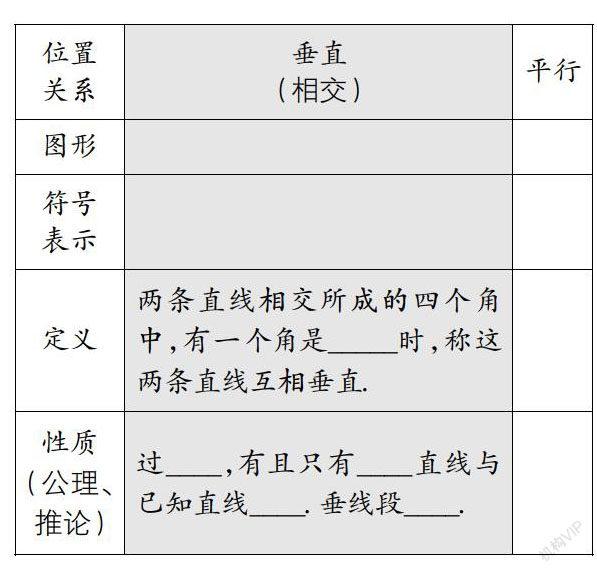
請每個學生各自完成下列表格中的第二列（陰影部分）：

本處筆者安排學生自己獨立完成，以此促使學生在自己的思維基礎上進行基礎概念的總結和回顧，這樣不僅鞏固了知識，還啟發(fā)了學生對相應思想和方法的思考.

1. 小組交流，合作協(xié)作提升

學生之間的差異是客觀存在且無法避免的，為了減小這種差異帶來的負面效應，小組合作是一種非常有效的教學策略，教師可以通過小組交流的形式，讓學生在合作的情況下協(xié)作提升相應的基礎環(huán)節(jié)，與此同時還可以發(fā)現新的問題和不足.

2. 成果展示，評價激勵成長

結合小組交流的實際情況，讓學生進行成果展示，展示的過程不僅僅是為了校對一下學生的自主學習情況，還啟發(fā)了學生對類比法的自發(fā)思考，以此服務于平行線的研究.

到這個環(huán)節(jié)，筆者在PPT中展示出“類比：我們用研究垂線的方法來研究平行線”，并直接引入這節(jié)課的主題“平行線”.

3. 活動初體驗，智慧巧啟迪

結合學習金字塔理論的研究，學生“做中學”或“實際演練”的學習效率可以達到75%. 因此，在教學過程中，教師要善于為學生創(chuàng)設一個實實在在“做”或“演練”的機會，讓學生真正在深入的體驗中收獲知識與技能，啟迪思想與智慧，達成輕松、愉悅、高效的學習效果，而智慧之門也正好在這樣的氛圍中悄悄地開啟. 就本節(jié)課而言，筆者采用體驗兩步走：

（1）活動體驗，建構新概念

生活中很多物體給我們以線的形象，比如細長的木條可以看成一條線段. 為此，我們可以課前將木條a，b與木條c釘在一起做成如1圖所示的小裝置，上課發(fā)給學生.

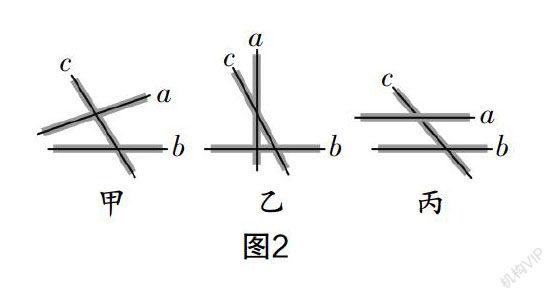
讓學生通過轉動a，直線a從在c的左側與直線b相交逐步變?yōu)樵谟覀扰cb相交. 并讓學生再次轉動，讓學生在轉動的過程中找出直線a與直線b有哪幾種位置關系.

學生在不斷的實踐體驗中得出如圖2所示的幾種情況，即甲中直線a和直線b的位置關系是相交；轉動直線a，當轉動到乙圖位置時，直線a和直線b的位置關系是垂直（此處筆者可以引導學生回答垂直和相交之間的關系，學生在筆者的引導下，可以獲知垂直是相交的特殊情況）；當學生再次轉動直線a，在轉動過程中發(fā)現有一種情況是直線a與直線b不相交，如圖丙所示. 在學生的親自體驗下，我們很快就構建了直線a和直線b的位置關鍵，即今天所要學習的“平行線”. 即在同一平面內，不相交的兩條直線叫作平行線.隨后筆者再通過PPT為學生展示如圖3所示的兩條平行線，并介紹相關符號，即兩條傾斜的平行線段“∥”，如直線a與直線b平行，記作：“a∥b”，讀作：“a平行于b”.

（2）思維體驗，鞏固新概念

為了更好地激發(fā)學生對平行線的理解，筆者又從兩個思維層面來啟發(fā)學生的思考和參與.

①生活鏈接. 筆者通過問題來啟發(fā)學生對生活中的平行線進行搜索，即提問學生：生活中有很多的平行線，你能舉例嗎？此時學生的思維是開放的，學生要充分收集生活經驗中的平行線，這樣既能達到充分激發(fā)學生對平行線的理解和生活的對接，還能達成暴露學生實際問題的效果，而且學生的智慧也在該處得到有效的增長. 學生舉出很多的例子，比如黑板的對邊，鐵路的軌道，等等. 而每個學生想出來的結果又不一樣，以此促使學生通過交流合作來提升他們對平行線的展示效果.

②概念再深. 其實在平行線概念的構建中，最難的環(huán)節(jié)是對定義中的“在同一平面內”的理解，為此，筆者在此采用如下的問題鏈來達成：

問題1：請同學們思考一下，定義中的“在同一平面內”這個條件是否可以省略？如果不可以，你能在這個教室中找到明顯的反例嗎？

問題2：在同一平面內兩條直線的位置關系有幾種？（相交和平行）

問題3：相交和平行的本質區(qū)別是什么？（相交有一個公共點，平行沒有公共點）

在問題的引領下，學生可以建構較為健全和系統(tǒng)的“平行線”的定義，到此，筆者再通過“找平行線”來全面提升相應的認知深度.

例題：如圖4，在長方體中找出和CD平行的棱，并用符號把它們表示出來. 和AA′平行的棱又有哪些？

技能真訓練，智慧真挑戰(zhàn)

學有所用，學有活用，是數學學習的關鍵所在，也是課堂教學的智慧所在. 教師要在平時的教學過程中將所學的知識與技能巧妙地銜接到實際應用之中，讓學生在實實在在的靈活應用中達成知識與技能的鞏固和提升. 而在本節(jié)的教學中，我們就是需要引導學生學會畫已知直線的平行線，并讓學生在作圖的過程中掌握作圖技巧，提升作圖技能，建構新認知和新技能. 在此，筆者采用以下幾個環(huán)節(jié)進行一一突破.

1. 作圖訓練

如果現在有一條直線a和直線a外一點P，你能利用直尺和三角板過點P畫直線a的平行線嗎？如圖5所示，嘗試畫一畫，然后小組內討論畫法.

為了提升學生參與作圖的積極性，筆者在學生作圖的過程中巡視學生的作圖情況，并引導學生進行討論. 隨后讓小組派2個代表交流展示，一人介紹畫法，一人展示畫法. 這樣的展示一方面反映了學生的思維成果，另一方面反饋學生對相應技能的掌握情況. 如果在作圖的過程中存在一定的不足和缺陷，筆者再進行平行線畫法的補充和完善. 隨后再提問學生：“這樣的平行線可以畫幾條？”學生回答：“一條. ”

2. 作圖提升

為了進一步通過訓練來提升學生的作圖技能，并在實踐中總結出平行公理，筆者再進行第二次的作圖訓練，以此達到作圖再提升的效果. 如下：

現在在直線a，b外再取一點Q，請你過Q點畫出直線a的平行線，如圖6所示，這樣的平行線可以畫幾條？

在學生作圖完成后，筆者請他們相互交流一下，并詢問他們可以得出什么結論. 學生隨即交流起來，筆者請學生回答.

生1：經過一點，有且只有一條直線與這條直線平行.

師：這個點在哪兒？

生2：直線外.

師：誰能補充完善一下？

生3：由此可以發(fā)現，經過直線外一點，有且只有一條直線與這條直線平行.

師：很好，這就是我們今天所學的平行公理，那么請同學們再來觀察同時和直線a平行的直線b和c，它們的位置關系是什么？你又發(fā)現了怎樣的結論？請大家交流一下.

同樣在筆者的引導下，得出平行公理的推論：如果兩條直線都與第三條直線平行，那么這兩條直線也互相平行.

■ 方法再總結，智慧再生長

“授之以漁”是教學的策略所在，但是如何達成高效的授之以漁的效果，關鍵在于授漁的過程. 教師需要站在學生的角度去分析問題、解決問題，甚至要學會應用解決問題過程中建構起來的方法與技能去解決更多的一類問題，達到與生共漁的效果. 比如在這節(jié)課的教學過程中，我們就要引導學生利用已學的知識來解決新的問題，并善于總結解決過程中的方法與思想等，讓學生真正學會如何學習.

1. 證明平行公理的推論

師：數學是講究嚴謹性的，我們一起來證明我們發(fā)現的結論. 假設直線a和直線b是不平行的，那么它們的位置關系是什么？

學生齊聲：相交.

師：不妨設它們的交點為G，這時過G點就有直線a，b兩條直線和直線a平行，而經過直線外一點，有且只有一條直線與這條直線平行.因此，你可以得出什么結論？

生：所以假設不成立，故直線a和直線b不可能相交，一定互相平行.

師：我們把這個結論稱為平行公理的推論.你能用符號語言來表示這個推論嗎？

2. 應用平行公理和推論

師：現在請同學們在平面內畫三條直線，數一數公共點的個數. 想一想，怎樣才能做到不重不漏. 畫完后小組內討論交流，結束后小組派代表交流展示.

在這個環(huán)節(jié)中，引導學生進行小組討論，讓學生注重不同情況的分析和對比，在分類討論中將問題一一解決，即我們數學中最為重要的思想方法之一——分類討論法.

3. 總結課堂知識與方法

無論是新授課還是復習課，課堂總結是必不可少的，而這個總結的過程必須充分體現生本主體，只有學生自己總結出來的內容才是學生真正掌握的內容，只有學生暴露出來的問題才是學生真正存在的問題. 在這里，我們一方面要讓學生自我回憶平行線的定義、公理及其推論，還要引導學生應用類比的方法來反思本節(jié)課的教學內容和思想方法. 于是，筆者讓每個學生回憶本課內容，補全表格. 讓學生在實實在在的自我總結和整理的過程中提升對知識與技能的鞏固，也讓學生在總結的過程中更深刻地感悟分類討論法和類比法這兩種數學思想方法，以此促使學生學習能力的真正提升.

上文就是筆者努力實踐和研究的情智課堂，即用情景、情感促動學生的學習，讓學生的主體地位得到充分的體現，以此促使學生智力的提升，建構智慧型的數學學習環(huán)境，讓學生在輕松愉悅的實踐中生長自己的智慧.