創設問題情境引導學生自主學習的幾種方式

寧夏彭陽縣第三中學 (756500)

杏望春

?

創設問題情境引導學生自主學習的幾種方式

寧夏彭陽縣第三中學 (756500)

杏望春

在教學中要真正體現學生學習的主動性，就必須使認知過程是一個再創造的過程，使學生在自覺、主動、深層次的參與過程中，實現發現、理解、創造與應用，在學習中學會學習，而創設問題情境，使學生產生明顯的意識傾向和情感共鳴，仍是主體參與的條件和關鍵.本文就此問題談幾點膚淺的認識，以向同行求教.

1 創設問題情境的主要方式

1.1 創設應用性問題情境，引導學生發現數學命題(公理、定理、性質、公式)

案例1 在《基本不等式》的一節教學中，可設計如下兩個實際應用問題，引導學生從中發現基本不等式的定理及推論.

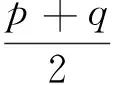
今有一臺天平兩臂之長略有差異，其他均精確.有人要用它稱量物體的質量，只需將物體放在左、右兩個托盤中各稱一次，再將稱量結果相加后除以2就是物體的真實重量.你認為這種說法對不對？如果不對的話，你能否找到一種用這臺天平稱量物體重量的正確方法？

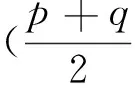
以上兩個應用問題，一個是經濟生活中的問題，一個是物理中的問題，貼近生活 ，貼近實際，給學生創設了一個觀察、聯想、抽象、概括，數學化的過程，在這樣的問題情境下，再注意給學生動手動腦的空間和時間，學生一定會想學，樂學、自主學.

1.2 創設趣味性問題情境，引發學生自主學習的興趣

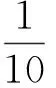
讓學生觀察這兩個數列的特征引出等比數列的定義，使學生興趣十分高漲，很快就進入了主動學習的狀態.

1.3 創設開放性問題情境，引導學生積極思考

案例3 直線與二次曲線的位置關系是解析幾何的重點內容，它融匯了較多的知識，涉及到眾多的思想方法.在這節的習題課上，可設計如下的問題情境：直線y=2x+m與拋物線y=x2相交于A,B兩點，_______，求直線AB的方程.請你補充恰當的條件，使直線方程得以確定.

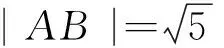
涉及到的知識有韋達定理，弦長公式、中點坐標公式、拋物線的焦點坐標，兩直線相互垂直的充要條件等等，學生實實在在的進入了“狀態”.

1.4 創設直觀性圖形情境，引導學生深刻理解數學概念

案例4 “充要條件”是高中數學的一個重要概念，并且是教與學的一個難點，如設計以下四個電路圖，視“開關A的閉合”為條件A,”“燈泡B亮”為結論B,給充分不必要條件、充分必要條件、必要不充分條件、既不必要也不充分條件以十分貼近，形象的詮釋，則使學生興趣盎然，對“充要條件”的理解入木三分.

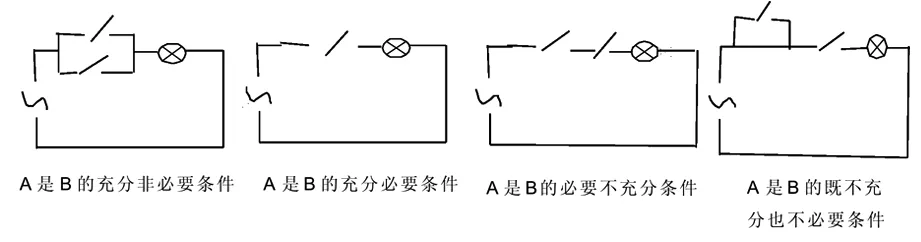
1.5 創設新奇懸念情境，引導學生自主探究

案例5 在“拋物線及其標準方程”一節的教學中，引出拋物線的定義“平面上與一個定點F和一條定直線l的距離相等的點的軌跡叫做拋物線”之后，設置這樣的問題情境：初中已學過一元二次函數的圖像是拋物線，而今定義的拋物線與初中學過的拋物線從字面上看不一致，它們之間有某種內在的聯系，你能找出內在的聯系嗎？

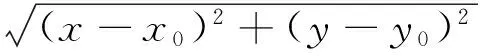
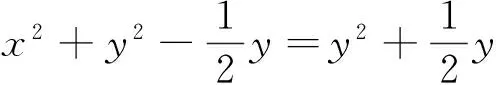
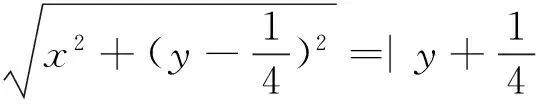
這個教學環節對訓練學生的自主探究能力，無疑是非常珍貴的.

1.6 創設疑惑陷阱情境，引導學生主動參與討論

(A)P到左焦點的距離是8

(B)P到左焦點的距離是15

(C)P到左焦點的距離不確定

(D)這樣的點P不存在.

教學時，根據學生平時練習的反饋信息，可有意識的出示如下兩種常見的錯誤解法：

解法1：設雙曲線的左、右焦點分別為F1, F2，由雙曲線定義得|PF1|-|PF2|=±10.∵|PF2|=5，,∴|PF1|=|PF2|+10=15，故正確結論為B.

錯解2：設P(x0,y0)(為雙曲線右支上一點，則|PF2|=ex0-a,由a=5，|PF2|=5，得ex0=10，∴|PF1|=ex0+a=15，故正確結論為B.

然后引導學生進行討論辨析，若|PF2|=5，|PF1|=15，則|PF1|+|PF2|=20，而|F1F2|=2c=26，即有|PF1|+|PF2|<|F1F2|,這與三角形兩邊之和大于第三邊相矛盾，可見這樣的點P不存在，因此正確的結論應該是D.

進行上述引導，讓學生比較定義，找出了錯誤產生的原因是忽視了雙曲線定義中的限制條件，所以除了考慮條件||PF1|-|PF2||=2a，還要注意條件a

通過上述問題的辨析，不僅是學生從“陷阱”中跳出來，增強了刺激，更主要的是能使學生參與討論，在討論中只覺得辨析正誤，從而增強防御“陷阱”的經驗，取得學習的主動權.

1.7 創設已有知識的問題序列，引導學生自己獲取新知識的生長點

案例7 在《曲線和方程》的教學中，對于“曲線的方程”和“方程的曲線”概念的引入，可利用函數的圖像設計如下問題序列：

①下列各圖中哪些能作為函數的圖像？

②如何修改可作為函數的圖像？

③再添上圖下的解析式，并問：圖與式相一致嗎?請改圖形(或改關系式)使兩者相對應.

④既然圖像與解析式存在著這種對應的關系，怎樣反映這種對應的關系呢？

至此，學生對“曲線”與“方程”的關系有了一些初步的認識，在此基礎上指導學生閱讀課本，學生就能夠理解曲線和方程的“純粹性”及“完備性”的含義，也就理解了什么是“曲線的方程” 和“方程的曲線”.

1.8 編擬“導學案”引導學生閱讀自學

案例8 在數學選修2《簡單幾何體的結構》一節中，由于概念較多，內容又與實際生活相貼近，可擬以下的“導學案”，讓學生閱讀自學：

①從課本所給的圖片中，你能找出它們的幾何特征并進行分類嗎？

②聯系實際生活，想想你還見過如圖片中的幾何體嗎?

③這些幾何體有什么特征，你能通過閱讀課文對它們進行歸納辨析嗎？

④將你歸納的結論形成知識網絡，課堂上發言.

通過上述所設計的學案，讓學生先學，課堂上再講，會加深學生對課本的理解，提高了先學的效率.

2 創設問題情境的原則

創設情境的方法很多，但必須做到科學、適度，具體地說，有以下幾個原則：

①要有難度，但必須在學生的“最近發展區”內，使學生可以“跳一跳，摘桃子”；②要考慮到大多數學生的認知水平，應面向全體學生，切記專為少數人設置；③要簡潔明確，有針對性，目的性，表達簡明扼要清晰，不要含糊不清，使學生盲目應付，思維混亂；④要注意時機，情境的設置時間要恰當，尋求學生思維的最佳突破口，要少而精，做到教者提問少而精，學生質疑多且而深.

3 幾點體會與認識

3.1 要充分重視“問題情境”在課堂教學中的作用

問題情境的設置不僅在教學的引入階段要格外注意，而且應當隨著教學過程的展開而成為一個連續的過程，并形成幾個高潮，通過精心設置問題情境，不斷激發學習動機，是學生經常處于“饑渴”的狀態，給學生提供學習的目標和思維的空間，學生自主學習才能真正成為可能.

3.2 在引導學生自主學習中加強學法指導

為了在課堂教學中提高教學效率，打造有效課堂的課堂教學，從發展性的要求來看，不僅要讓學生“學會”數學，而且更重要的是“會學”數學，學會學習，具備在未來的工作中，科學地提出問題，探索問題，創造性的解決問題的能力.要結合教學實際，因勢利導，適時的進行學法指導，使學生在自主學習中，逐漸領會和掌握科學地學習方法，當然，自主學習也離不開教師的指導作用.這種作用主要在問題情景設置和學法指導兩個方面，學法指導有利于提高學生自主學習的效益.

3.3 注重情感因素是啟動學生自主學習的關鍵

要引導學生自主學習，動機、興趣、情感、意志、性格等非智力因素起著關鍵的作用，只有把智力因素和非智力因素有機的結合起來，充分調動學生認知的、心理的、生理的、情感的、行為的、價值的等各方面因素，讓學生進入一種全新的境界，學生自主學習才能達到比較好的效果，這就需要在課堂教學中，做到師生融洽，感情交流，充分尊重學生的人格，關心學生的發展.