建構主義在數學教學中的實踐
李婷婷
摘 要:情境教學以創設情境為基礎, 提出問題為手段, 在教學過程中, 向學習者提供解決問題的原型, 強調具體情境中形成的具體經驗背景對建構的重要作用,教師在課堂上應展示與實際問題解決相類似的探索過程,來解決問題。 關鍵詞:情境教學;實際問題;解決問題
一、問題提出
傳統的數學課堂教學重知識的傳授,教師的教學多是在“灌輸”、“填充”,學生就是“接受”、“吸收”知識。目前很多在校的學生往往感到課堂上教的數學知識,與他們的現實生活向脫離,學到的知識很死,難以將學到的知識靈活使用,對課學習興趣缺乏。
在當代的教育思潮中,建構主義學習理論的興起與發展,在世界范圍內產生影響,給教育帶來變革和新的發展活力。建構主義認為,知識并不是對現實的準確表征 ,而只是一種解釋和假設。學習者根據自己的經驗背景 ,以自己的方式建構對知識的理解,不同的人看到的是事物的不同方面 ,因此對于世界的理解和賦予意義由每個人自己決定 ,而不存在唯一標準的理解。學習不是簡單的信息積累 , 更重要的是新舊知識經驗的沖突以及由此而引發的認知結構的重組。
建構主義理論倡導的教學模式有情境性教學、支架式教學、拋錨式教學等。這些教學方法引導學生自主學習、探究發現,注重發展學生的思維和解決問題的能力,培養創新精神和創新能力。
本文就具體教學實踐來談談,建構主義理念下的情境教學法在數學教學中的嘗試。
二、情境教學
情境教學可激發學生多方面的興趣,及時有效地吸引學生的注意力,并使學生在試圖回答問題的過程中建構自己的知識體系。創設情境與設問緊密相連,課堂提出的問題應經過周密的組織,具有邏輯順序,圍繞一個教學目標層層鋪墊,步步深入,符合學生的認知規律。在教學中使用情境教學,往往會聯系其他教學模式,如支架式教學。即情景教學模式常常也是維果斯基提出的“昀近發展區”思想的實踐。“昀近發展區”是指學生的“潛在發展水平”,在此水平上,學生還不能獨立完成學習任務即解決問題,但經過啟發,幫助和努力,就能完成任務。數學教學中教師可以通過提供相關模型,進行現場操作演示,設置情境進行鋪墊等方式,來建立“昀近發展區”,使學生達到解決問題的水平。
三、以實際教學案例淺析情境教學的實施
1.創設問題情境
創設的情境的目的在于營造良好的思維氛圍,調動學生的興趣,激發學生的情感。有效的情境要貼近現實生活,以學生的興趣和思維為起點,提出問題,遵循學生認識的規律。
如《銳角三角函數的應用》的教學目標是培養學生能夠在實際問題中建立銳角三角函數模型,解決實際問題。教學的開頭,以問題情境導入:
“同學們,如果有一天你想要買房子,那么你在買房子的時候會考慮哪些因素呢?”“買房子”是當代的熱點問題,學生們耳濡目染,對這個問題的背景一點不陌生,反而很有興趣。學生的答案考慮了很多方面:價格、大小、地點、樓層、交通……學生們說得挺全面,這時進一步追問:“你會選擇一個照不到陽光的房子嗎?”這個是很多學生會忽視但又很實際的問題,提出這個問題學生很快就能進入這節課教學中心——樓房采光問題。
進入主題后,很自然地向學生們展示一個具體實際問題情境:
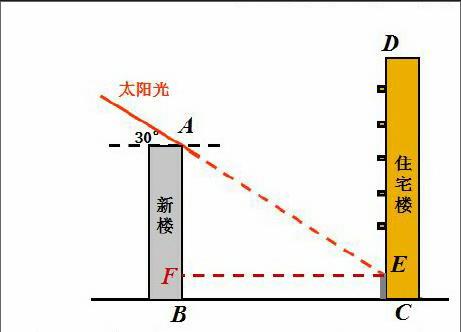
某住宅小區有一朝向為正南方向的住宅樓 ,該住宅樓的一樓是高 6米的小區超市 ,超市以上是居民住房。在該樓的前面 15米處要蓋一棟高 20米的新樓,當冬季正午的陽光與水平線的夾角為 30°時,問: 超市以上的居民住房采光是否會受到影響,為什么?
看到這個問題,學生很快在大腦中構想實際場景,但是大多數學生對于處理其中的位置和幾何關系是困難的,對情境的理解相當模糊。所以教師要想辦法化難為易,將這個問題分解逐步解決。
2.探究過程
為了解決上面的問題,先來看看下面的問題。
問題一:某住宅小區有一朝向為正南方向的住宅樓,該住宅樓的一樓是高 6米的小區超市,超市以上是居民住房。在該樓的前面要蓋一棟高 20米的新樓,當冬季正午的陽光與水平線的夾角為 30°時,問: (1)若要使超市采光不受影響,兩樓應相距多少米較為合理?
教師這時在課堂用實物模型模擬實際場景,指導學生經歷實際問題解決的探索過程。教師擺出新樓和住宅樓的模型,然后在新樓一側開燈照射(可以用床頭燈做教具)。學生分組,自己動手移動新樓的位置,看看怎樣能讓超市不被新樓的影子覆蓋到。學生合作討論:新樓的位置對住宅樓的采光有什么影響。在這一教學過程中,學生很直觀地理解題目,而且能夠抓到一個關鍵點——臨界值,在移動的過程中,很容易發現當新樓距離住宅樓的某個位置時,影子恰好剛剛離開超市,此后繼續遠離,都不會有影子蓋在超市上,而如從這個位置接近住宅樓,就會有影子覆蓋。
由此,讓學生將這個實際問題抽象為幾何圖形,并解決問題,就不困難了。用實物模型和課件圖示共同構建出問題情境,直觀形象,易于理解和接受,符合學生的認知,也讓學生體驗了問題解決的探究過程。
問題二:某住宅小區有一朝向為正南方向的住宅樓,該住宅樓的一樓是高 6米的小區超市,超市以上是居民住房。在該樓的前面要蓋一棟高 20米的新樓,當冬季正午的陽光與水平線的夾角為 30°時,問: (2)若新樓的影子恰好落在超市 1米高的窗臺處,兩樓應相距多少米?
在第一個問題的基礎上,增加條件,加深學生對問題思考,讓學生分組合作,通過動手操作,探究討論,獨立解決問題。
解決第一題后,學生對題目中的“恰好”的含義的理解,并不困難。如圖所示:
此時,回到昀初的問題,學生再看這個問題已經不模糊了,腦中能清晰勾畫出平面模型圖示。而且,開始問題的解決與第二個問題的“恰好”的理解有緊密關系。在做好鋪墊的基礎上,來解決這個問題,是順理成章的事。
課堂上學生在情境中學會將實際問題轉化為銳角三角函數模型,體會到生活與數學息息相關,可以將方法運用到更多生活實際問題中。
四、結語
創設情境對于教學非常重要,情境之于知識,猶如湯之于鹽。情境教學以創設情境為基礎 , 提出問題為手段 , 在教學過程中, 向學習者提供解決問題的原型 , 強調具體情境中形成的具體經驗背景對建構的重要作用,教師在課堂上應展示與實際問題解決相類似的探索過程,來解決問題。
情境教學能夠激發學生的興趣,在探究過程中培養思維能力,真正發展學生解決問題的能力,并能營造良好的學習氛圍,使學生體會學習的樂趣。

