凸多邊形與其內接多邊形的面積關系

王來全,李 碩，夏米西努爾·阿布都熱合曼

(1.昌吉職業技術學院 基礎部,新疆 昌吉 831100;2.昌吉學院 數學系,新疆 昌吉 831100；3.新疆大學 數學與系統科學學院,新疆 烏魯木齊 831146)

?

凸多邊形與其內接多邊形的面積關系

王來全1,李 碩2，夏米西努爾·阿布都熱合曼3

(1.昌吉職業技術學院 基礎部,新疆 昌吉 831100;2.昌吉學院 數學系,新疆 昌吉 831100；3.新疆大學 數學與系統科學學院,新疆 烏魯木齊 831146)

圖案設計和工程建筑經常會涉及到圖形的面積問題,研究了任意凸多邊形與其內接多邊形面積間的等比關系,并給出了等比關系式,數值模擬驗證了這一關系式的正確性.最后,討論了棱柱體在定義條件下的體積問題.

凸多邊形;內接多邊形;正棱柱體;面積

研究物體的形狀、大小和相互位置的科學叫幾何學[1].幾何圖形一般是從客觀實際中抽象出來的,研究幾何圖形的性質,其中最重要的目的之一,在于應用這些性質來解決實際問題.對于面積而言,在工農業生產或日常生活方面,應用都極為廣泛.例如:農業上的畝產量計算[2],興修水利,密植、輪值,工業上安裝機器,樓層與倉庫的設置,測量各種建筑物的表面積容積[3-4],客廳、墻面等花紋底色圖案的設計問題都與面積的計算或作圖等有著密切的聯系.因此,研究圖形的面積問題,是平面幾何中的重要內容之一.我們應用平面幾何的相關理論,將多邊形的各邊中點順次相連組成新的圖形,重點討論了組成的新圖形與原圖形的面積關系,揭示了在這種定義形式下凸多邊形與其內接多邊形的面積關系.

1 預備知識

定義1 在平面V2中,對任意凸N邊形,順次連接各邊中點所成的圖形,記為該N邊形的C1形,順次連接C1形各邊中點所成的圖形記為C2形,…，順次連接Ci形各邊中點所成的圖形記為Ci+1形(i∈N+).

定義2 在空間V3中，N棱柱的上下平面的C1形組成的棱柱體為N棱柱的X11形棱柱體，X11形棱柱體的上下平面的C2形組成的棱柱體為X22形棱柱體,…,Xii形棱柱體的上下平面的Ci+1形組成的棱柱體為Xi+1i+1形棱柱體(i∈N+).

定義3 在空間V3中，由N棱柱體(N+2面體)的各側棱中點和上下平面的C1形組成的3N+2面體，記為該棱柱體的Y形體.

2 主要結果

定理1 在平面V2中,任意四邊形的面積S0與該四邊形的Ci形面積Si間有等比關系,且有

證明 任取一個四邊形A1A2A3A4,A1A2的中點為B1,A2A3的中點為B2,A3A4的中點為B3,A4A1的中點為B4,則B1B2B3B4,設A1A3=x,A2A4=y,設ΔA1A2A3的高為h1,ΔA1A4A3的高為h2,ΔA1A2A4的高為h'1,ΔA2A3A4的高為h'2,則有

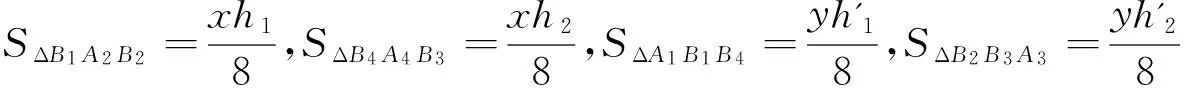
SΔB1A2B2+SΔB4A4B3+SΔA1B1A4+SΔB2B3A3=

注1 定理1還可以用割補、平移法證明,根據數學歸納法,可以得出下面的推論.

推論1 在V2中，任意N邊形的面積S0與該N邊形的Ci形的面積Si間有如下等比關系

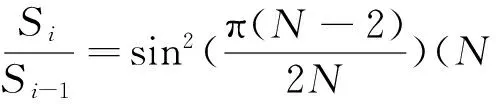
當N→∞時,Si=S0,即圓與圓的Ci形的面積是相等的[5].

定理2 在V3中，任意N棱柱體的體積V0與N棱柱的Xii形棱柱體的體積Vi間有如下關系.

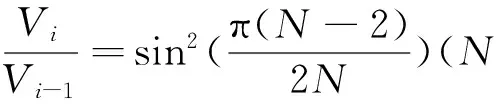
定理3 在V3中,任意正N棱柱體與其Y形體的體積比為一定值,且有

其中V20表示任意正N棱柱體的體積,V21表示該正N棱柱體的Y形體積.

證明 假設組成任一正N棱柱體的N邊形的邊長為a,正N棱柱的高為h,則正N邊形的面積為

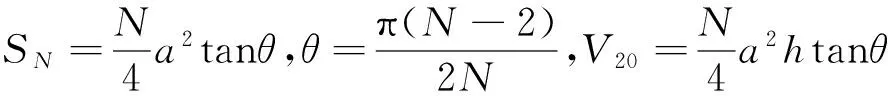
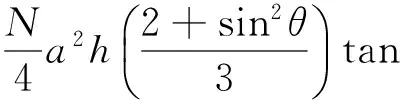
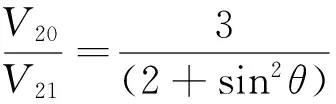
當N→∞時,V20=V21,可認為圓柱體與它的Y形體的體積相等.

下面通過兩個具體的實例(N=6，N=7)來說明上述推論的正確性．

3 數值模擬

CAD軟件可以幫助設計人員計算、信息儲存和繪圖工作.應用CAD軟件構造出任意一六邊形(圖1)和任意一七邊形(圖2)，通過CAD的查詢命令計算了這一六邊形與七邊形的面積與其對應的內接圖形的面積,其中S0表示這一任意六邊形和七邊形的面積,Si表示六邊形和七邊形的Ci形面積(i>1),其結果如表1所示，進一步驗證了推論的正確性.

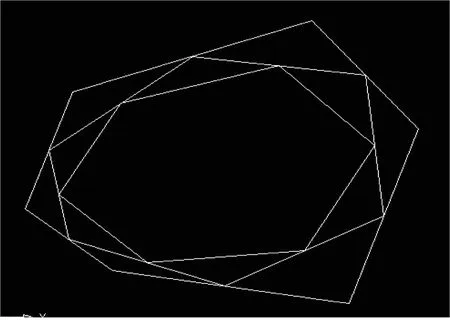
圖1 任取一六邊形及其內接圖形

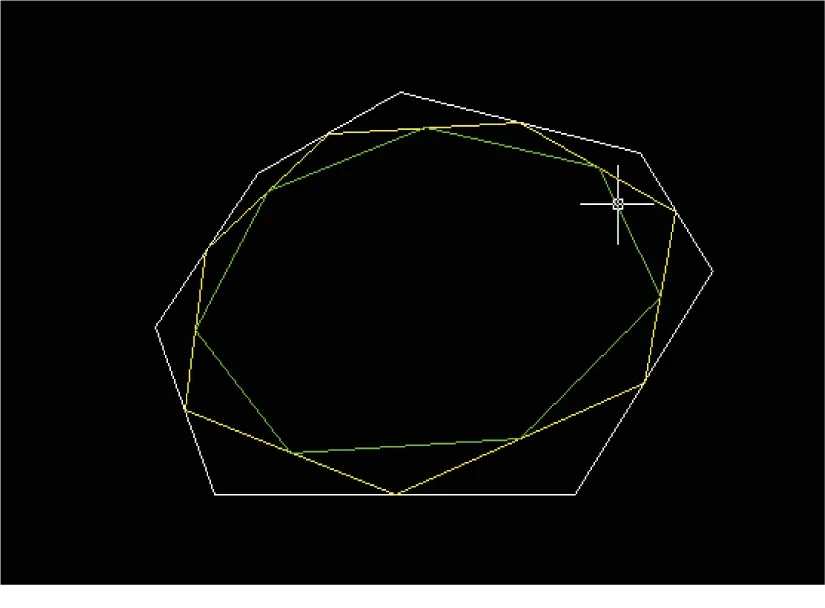
圖2 任取一七邊形及其內接圖形

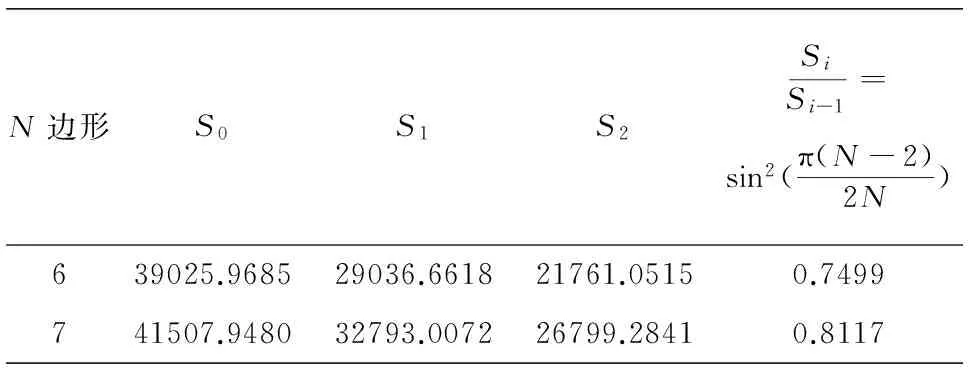
表1 六邊形和七邊形的面積與內接圖形的面積關系

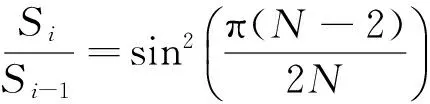
4 結論

通過探討任意凸N邊形內接圖形的面積與原圖形的面積間的等比關系,并用CAD軟件進行模擬，模擬效果良好．這種在新定義下實施的面積計算方法,對以后一些圖案的設計有一定的啟示.所以,具體地求任意凸多邊形及其內接多邊形的面積會在建筑工程造價等方面有很大的幫助,也將在一定程度上對推動機械制造和工程建筑業的進步有一定的意義.

[1]高孝忠,羅淼.解析幾何[M].北京:清華大學出版社,2011.

[2]中學數學課程教材研究開發中心.新課標數學九年級[M].北京:人民教育出版社,2010.

[3]呂林根,許子道.解析幾何[M].北京:高等教育出版社,2010.

[4]曾令淮,段輝明,李玲.高等代數與解析幾何[M].北京:清華大學出版社,2014.

[5]同濟大學數學系.高等數學[M].北京:高等教育出版社,2014.

[6]張小平,張國清.建筑工程CAD[M].北京:人民交通出版社,2007.

(責任編輯:陳衍峰)

10.13877/j.cnki.cn22-1284.2016.08.015

2016-03-12

國家自然科學基金“人口流動對艾滋病傳播影響的動力學模型研究”(11261056);昌吉職業技術學院自然科學基金“具有干預措施的HIV/AIDS傳播模型的建立與研究”(CJZY2015026)

王來全,甘肅定西人,講師.

王來全,E-mail:wanglaiquana@126.com

O182

A

1008-7974(2016)04-0047-03