互補問題中兩個定理的推廣
任佳盈
(長春工業大學 基礎科學學院,吉林 長春 130012)
?
互補問題中兩個定理的推廣
任佳盈
(長春工業大學 基礎科學學院,吉林 長春 130012)
利用簡單的數學工具,對互補問題中的兩個重要定理進行了推廣和證明,通過改變定理的某些條件,使得當條件變弱時,定理依舊成立.
互補問題;定理;推廣;非線性互補
互補問題首先由著名運籌學家、數學規劃的創始人G.B.Dantzig教授和他的學生R.W.Cottle于1963年提出.1964年,R.W.Cottle在其博士論文中第一次提出了求解它的非線性規劃算法.這一問題在初期被稱為“拼合問題”“基本問題”等.1966年,P.Hartman和G.Stampscchia提出了一個與互補問題密切相關的概念——變分不等式,1971年,Karamardian證實了非線性互補問題是變分不等式的一種特殊情形.變分不等式聯系著不動點理論、最優化理論、經濟學理論、最優控制論,而且在交通模型以及社會和經濟模型等方面有著廣泛應用.互補問題作為變分不等式的特例,也有廣泛的應用背景.
本文在前面研究的基礎上,對互補問題中的兩個重要結論進行了推廣,通過改變它的某些條件,使其條件變弱時,這個定理依然成立.這為以后定理的發展提供了基礎.
1 預備知識
引理1 設F:Rn→Rn是一個連續單調函數.如果存在y∈Rn和兩個正的常數M,C使得
(1)F(y)>0且c‖y‖ (2)對于任意的x,‖x‖1≥M?‖F(x)‖≤C‖x‖1. 則有Zε={x∈Rn:x≥0,F(x)≥0,xTF(x)≤ε}對于任意的x≥0,F(x)≥0是有界的. 引理2 假設ψ≤ψ(1),F為單調函數,x*是非線性互補問題的一個解,并且x(r)(0 h(‖x-y‖)≤〈x-y,F(x)-F(y)〉. 其中,h:[0,+∞]→[0,+∞]且h(0)=0,h(t)>0,當t>0時,并且存在ε,η>0使得h:[0,ε]→[0,η]是一個遞增的雙射.那么非線性互補問題有唯一的解x*,并且存在r0>0,使得當r∈[0,r0]時,有‖x*-x(r)‖≤h-1(nr2). 定理1的推廣 設F:Rn→Rn是一個連續的P*映射,則存在y≥0,F(y)>0,對于任意ε>0,Zε={x∈Rn:x≥0,F(x)≥0,xTF(x)≤ε}是有界的. 證明 用反證法證明.假設存在ε>0,Zε無界.則存在{x(k)}∈Zε,即 x(k)≥0,F(x(k))≥0,(x(k))TF(x(k))≤ 使得當K→+∞時,‖x(k)‖→+∞.由于 yiFi(x(k))+yiFi(y)≤ 其中,i=1,2,…,n. 定理2的推廣 假設ψ≤ψ(1),F為P*映射,x*是非線性互補問題的一個解,并且當r1>0時,x(r)(0 (2)如果F滿足條件 h(‖x-y‖)≤ 其中,當t>0時,h:[0,+∞]→[0,+∞]且h(0)=0,h(t)>0,并且存在ε,η>0使得h:[0,ε]→[0,η]是一個遞增的雙射,那么非線性互補問題有唯一的解x*,并且存在r0>0,使得當r∈[0,r0]時,有‖x*-x(r)‖≤h-1(cr2)(c≥0). 證明 (1)的證明與定理2的證明類似,作簡要證明.因為x(r)滿足Hr(x)=0,即 因為ψ≤ψ(1),所以 (2)h(‖x-y‖)≤ (1+τ)r2+r2=(2+τ)r2(τ≥0) 又因為h:[0,ε]→[0,η]是一個雙射并且h-1是遞增的,所以定理得證. 對變分不等式和非線性互補問題的研究,一般分為理論和算法.前者主要研究解的存在性、唯一性、穩定性和靈敏度分析;后者主要建立有效的求解方法及相應的算法分析.針對算法來說,主要有連續化方法、內點法、光滑(非光滑)方程算法、信賴域算法、效益函數法、投影收縮法等.本文在求解互補問題的光滑化方法過程中,對一些定理進行了擴展,旨在更弱的條件下,這類方法或對于誤差的估計依然成立.這對于互補問題方法的研究有意義. [1]Mounir Haddou, Patrick Maheux. Smoothing Methods for Nonlinear Complementarity Problems[J].J Optim Theory Appl,2014,160:711-729. [2]韓繼業,修乃華,戚厚鐸.非線性互補理論與算法[M].上海:科學技術出版社,2006. [3]Haddou M. A NEW class of smoothing methods for mathematical programs with equilibrium constraints[J].Pac.J.Optim.,2009,5(1):86-96. [4]Haddou M. Asymptotic analysis for penalty and barrier methods in convex and linear programming[J].Math. Oper. Res.,1997,22(1):43-62. [5]Cottle R W, Pang J-S, Stone R E. The linear Complementarity problems[J].Classics in Applied Mathematics,2009,60(2):60-66. [6]修乃華,韓繼業.對稱錐互補問題[J].數學進展,2007,36(1):1-11. (責任編輯:陳衍峰) 10.13877/j.cnki.cn22-1284.2016.08.017 2016-03-15 國家自然科學基金項目“基于三維隨機模擬的傍河型水源地污染物遷移規律研究”(51278065);吉林省科技計劃項目“向量優化問題的路徑跟蹤算法研究”(20130101061) 任佳盈,女,山西運城人,長春工業大學基礎科學學院在讀碩士. TP399 A 1008-7974(2016)04-0052-02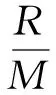
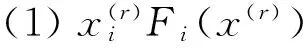
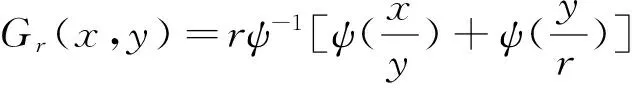
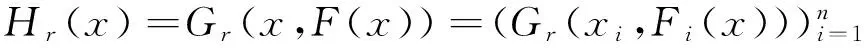
2 主要結果
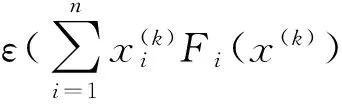

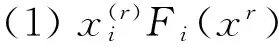
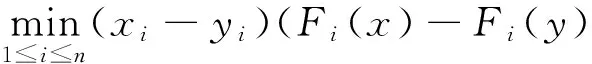
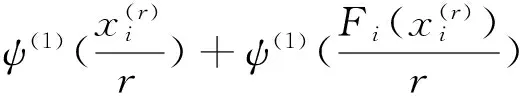

3 結束語

