基于SVD的地震資料去噪方法的研究和應用

崔少華，單 巍，趙慶平

(淮北師范大學 物理與電子信息學院，安徽 淮北235000)

?

基于SVD的地震資料去噪方法的研究和應用

崔少華，單 巍，趙慶平

(淮北師范大學 物理與電子信息學院，安徽 淮北235000)

利用信號和噪聲奇異值大小的差異，實現了奇異值分解算法去噪，通過對地震數據矩陣進行分解，得到按降序排列的奇異值矩陣，再選取與信號空間維數相同的奇異值個數進行重構，可以完全地恢復信號.采用兩條同相軸地震數據進行驗證，奇異值分解對于水平的或接近水平的同相軸去噪效果良好，對于傾斜的或彎曲的同相軸去噪效果欠佳，只有選取足夠的空間維數才可達到預期去噪效果.

奇異值分解；地震數據；信號空間維數

對地震資料進行噪聲衰減，提高信噪比，是地震資料中關鍵的一項任務，其中噪聲的衰減通常是利用有用信號和噪聲特性上的差異來進行分離，后續再對噪聲進行去除.各種去噪方法也是根據噪聲的特性不同而決定的.但實際地震資料中往往摻雜著與有效信號相互獨立的噪聲，也存在與有效信號相關的多次波的反射等干擾，在信號與噪聲頻率的特性不明顯的情況下，分離噪聲使用傳統的頻率域內濾波顯然是無法進行的[1].因此，奇異值分解算法(Singular Value Decomposition,SVD)就是在這種情況下產生的.

在實際地震資料中，SVD算法被廣泛應用于數據壓縮和隨機噪聲的壓制等方面，并且在這些方面的應用，奇異值分解有明顯的作用.

1 SVD的方法原理

1.1 SVD的原理

設矩陣X是由m個通道觀察值(每個通道上n點采樣數據)組成的數據陣.由數學知識可知，當矩陣X滿足一定條件時，可對X作如下分解變換[2]：

(1)

式中：U與V都是正交歸一陣，即：

UTU=UTU=Im,

VTV=VVT=In(其中I表示單位矩陣).

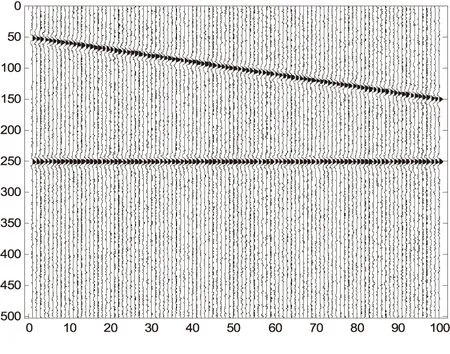
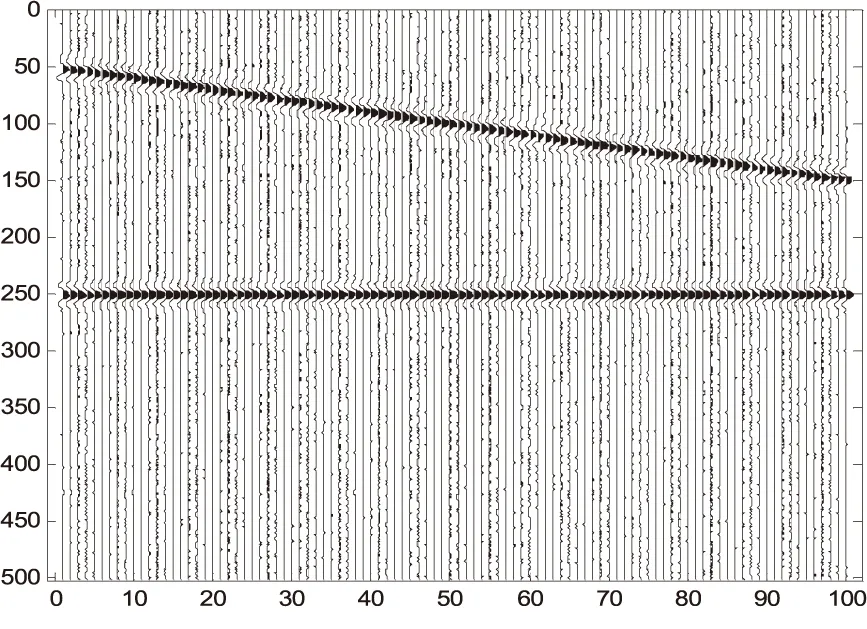
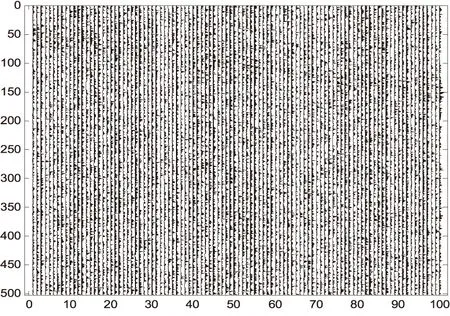
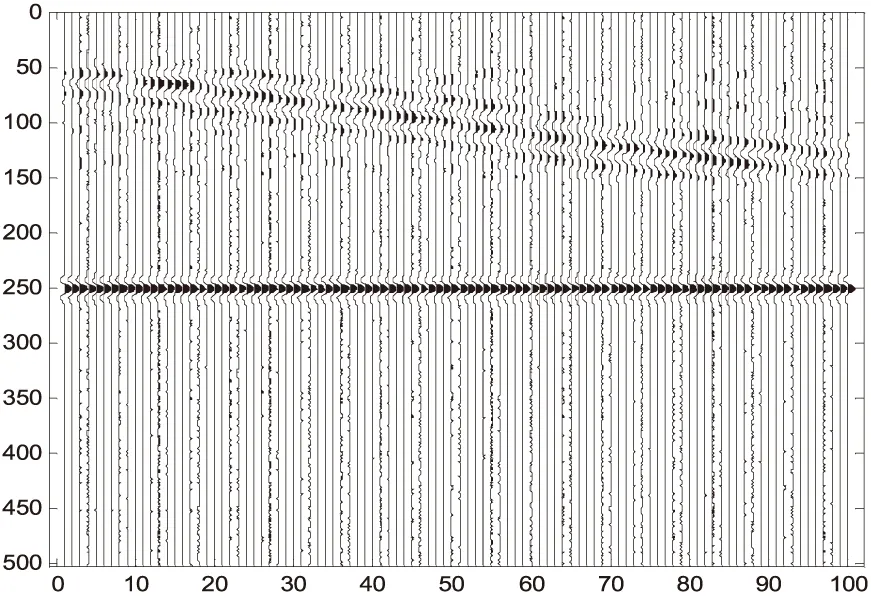
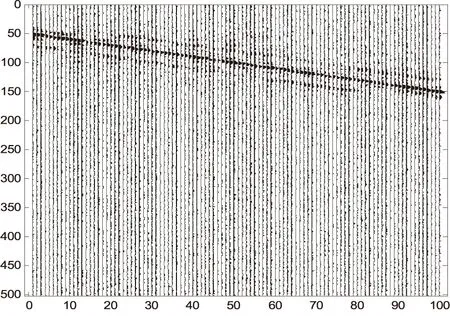
∑為準對角矩陣，在m

(2)

通常設σ1≥σ2≥…≥σm≥0，稱σi為奇異值.

如果記U=[u1,u2,…,um],V=[v1,v2,…,vn]，則式(1)可寫為：

(3)

式中：ui和vi稱為左、右奇異矢量，其維數分別為m×1和n×1.維數為m×n的原始數據就被分解成維數相同的m個子矩陣，這就是奇異值分解[3].

1.2 SVD去噪方法

假設存在一個二維的地震數據X，其有m道觀察值，每道有n個采樣點數據(m

(4)

接著在對X進行奇異值分解，利用式(1)可得：

(5)

式中：U,V分別為左右奇異矩陣，∑為奇異值矩陣.

由式(4)和奇異值分解σ1≥σ2≥…≥σm≥0的性質，可以將式(5)用另一種方式表達：

(6)

在奇異值矩陣中，∑S=diag[σ1,σ2,…,σp]就是地震記錄中信號矩陣的奇異值，∑N=diag[σp+1,σp+2,…,σm]就是地震記錄中噪聲矩陣的奇異值.

其中p=Rank(S)就是信號矩陣的秩，即信號空間的維數[7].因此，為了完全保真有效信號，就必須進行不小于p階的重構，將矩陣X的奇異值截斷，舍去噪聲空間的奇異值，進行P階的重構就可完全恢復信號[8]：

(7)

2 SVD去噪方法的應用

本次地震模型使用2條同相軸，其中1條水平同相軸，1條傾斜同相軸，地震子波采用峰值頻率為50Hz的Ricker子波，時域每道501個點共100道，采樣間隔1毫秒，結果如下圖所示.

圖1 原始二維地震記錄

圖2 含噪地震記錄

圖3 歸一化奇異值曲線

由圖3可知，第一個奇異值幅度遠遠大于其他奇異值，這實際上就是水平同相軸對應的奇異值.從第2到17個奇異值幅度明顯下降，且幅度都遠大于后面的奇異值，從18到100個奇異值，其變換緩慢，且幅度基本保持不變，因此，認為第1到17都是信號所對應的奇異值，從18到100個奇異值，是噪聲對應的奇異值，對該記錄進行17階重構，結果如下圖所示.

圖4 17階重構后結果

由圖4可知，通過17階的重構，可以將信號完全無失真地重構出來，在分離出來的噪聲中，幾乎不含有信號的能量，這一點也說明了，SVD只要選擇正確的信號空間維數，對其進行重構后，可以很好地分離噪聲，提高地震資料中的信噪比.

圖5 17階分離出噪聲

針對本次模型，使用前6個奇異值重構后，結果如下圖所示.

圖6 6階重構后結果

圖7 6階分離出噪聲

由圖6、圖7可知，6階重構將水平同相軸無失真地重構出來，將傾斜同相軸一部分重構出來，另一部分混合在噪聲里，無法將其和噪聲分離.已知該地震原始記錄的信號空間維數為17，因此當重構信號空間維數取得不夠時，無法完全重構非水平同相軸.

3 結論

SVD對水平同相軸的去噪效果優于對傾斜同相軸的去噪效果，甚至十分明顯.SVD利用了有效信號各道之間的相關性，各道數據之間相關性越強，奇異值分解后信號的能量就越集中，信號和噪聲就越好分離；反之，信噪可分性就較差.對水平同相軸，各道之間的相關性很強，往往只需要前面很少的幾個奇異值就可以完全恢復，并且隨機噪聲大量地被壓制；但是非水平同相軸(相關性減弱)卻往往需要較多的奇異值才能完全恢復，并且在恢復的過程中，引入較多的隨機噪聲.

[1]沈鴻雁,李慶春.線性域SVD地震波場分離與去噪方法[J].煤炭學報,2012,37(4):627-633.

[2]朱萍萍,李雙東,韓鈺.廣義正定矩陣的相關性質及其判定[J].通化師范學院學報,2015(6):26-27.

[3]崔業勤,高建國,丁國超.LLE重構和SVD分解的地震信號降噪方法[J].計算機工程與應用,2015.

[4]沈鴻雁,李慶春.奇異值分解地震縱、橫波波場分離與去噪方法[J].石油地球物理勘探,2012,47(5):690-697.

[5]彭更新,鄧曉東,滿益志,等.f-x域Cadzow濾波隨機噪聲衰減及其局限性分析[J].石油天然氣學報,2013,35(1):63-66.

[6]馬繼濤,王建花,劉國昌.基于頻率域奇異值分解的地震數據插值去噪方法研究[J].石油物探,2016(2).

[7]袁恩輝,陳鳳來,齊志斌,等.奇異值分解在去除特殊干擾波中的研究與應用[J].非常規油氣,2015,2(5):20-25.

[8]何希平,楊勁,劉波.信號的SVD重建模型及其應用[J].計算機工程與設計,2015(4):962-966.

(責任編輯:王海波)

10.13877/j.cnki.cn22-1284.2016.08.020

2016-06-14

安徽省高等學校自然科學研究項目(KJ2014B07)

崔少華，女，陜西咸陽人，講師.

P315

A

1008-7974(2016)04-0060-03