關于資產證券化中信用評級行為的分析
陳宗雯

中圖分類號:F830 文獻標識:A 文章編號:1674-1145(2016)10-000-02
摘 要 本文將運用演化博弈的方法分析資產證券化中信用評級的行為,并提出約束信用評級機構行為的建議。
關鍵詞 資產證券 信用評級 演化博弈
一、演化博弈模型的建立
在現實生活中,信用評級機構有不提供虛高評級(策略A)和提供虛高評級(策略B)行為選擇。假設只有兩個信用評級機構,則支付矩陣為:
其中,F為評級機構獲得的現有客戶收入,F>0;S為評級機構不提供虛高評級所獲得的聲譽收益,S>0;C為評級機構不提供虛高評級而造成客戶流失的收益,C>0;T是信用評級機構因提供虛高評級而繳納的罰款,T>0。支付矩陣顯示有四種情況:(1)機構1與2均實施策略A,則機構1與2在獲得正常營業收益F的基礎上還將增加良好聲譽所帶來的收益S;(2)機構1選擇策略A,機構2選擇策略B,則機構1在獲得正常營業收益F的基礎上,還將增加其良好聲譽所帶來的加倍收益2S,同時減少那些想通過違規手段通過信用評級的客戶的收益C;而機構2在獲得正常營業收益F的基礎上,還會增加想通過違規手段通過信用評級的客戶收益C,同時增加了因違規所繳納的加倍罰款2T;(3)機構1選擇策略B,機構2選擇策略A,該種情況的分析與情況二類似。在此不再贅述;(4)機構1和2均選擇實施策略B,則機構1和機構2均在獲得現有客戶收入F的基礎上減少罰款T。
二、演化博弈過程
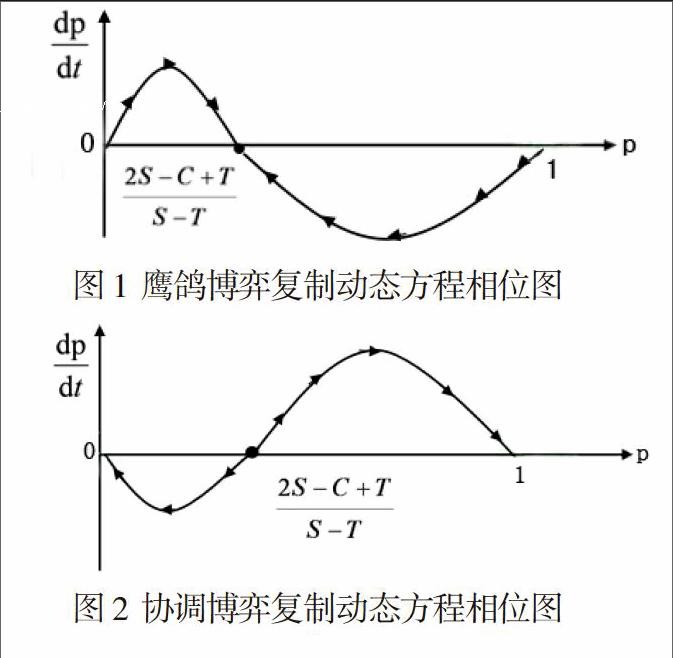
假設不提供虛高評級服務的信用評級機構占比為P,提供虛高評級服務的信用評級機構占比為(1-P),采取兩種策略博弈方的期望收益分別為u1和u2,整個群體的平均收益為u,則u1=F+S+(1-P)(S-C); u2=F-T+P(C-T); u=pu1+(1-P)(F-T),由以上式子可得復制動態方程F(P)=P(1-P)[2S-C+T-P(S-T)]。令F(P)=
0,則P*1=0,P*2=1,P*3=(2S-C+T)/(S-T),其中,0< P*3<1。上式所得到的三點只有滿足F(P*)<0時,才是進化穩定策略,其中,F(P)=(1-P)[2S-C+T-P(S-T)]+[2S-C+T-P(S-T)]+P(1-P)[2S-C+2T-S],將 P*1,P*2,P*3分別代入上式得:F(P*1)=2S-C+T;F(P*2)=C-S-2T;F(P*3)=(2S-C+T)(5+2T-C)/(S-T)
下面需要分情況討論:(1)當2S-C+T>0,2S-C+T>0,S-T>2S-C+T時,則F(P*1)>0,F(P*2)>0, F(P*3)<0,只有P*3=(2S-C+T)/(S-T)是演化穩定策略,形成鷹鴿博弈。這說明,當信用評級機構的競爭利益符合上述設定時,在長期的演進過程中,采取不提供虛高評級服務的信用評級機構的比例最終穩定在(2S-C+T)/(S-T)左右的水平, 但還有(C-2T-S)/(S-T) 的信用評級機構會選擇為發行機構提供虛高評級服務。這是一個相對比較穩定的狀態,實際情況將在該水平上下波動,如圖1所示。 (2)當2S-C+T<0,S-T<0,S-T<2S-C+T時,則F(P*1)<0,F(P*2)<0,F(P*3)>0,由上述三個不等式可知,只有P*1=0,P*2=1是演化穩定策略,此時形成協調博弈,其相位圖如圖2所示。當初始狀態位于區間[0,(2S+T-C)/(S-T)]時,復制動態會趨于穩定狀態P*1=0 即所有信用評級機構均為發行機構提供虛高評級服務;當初始狀態位于[(2S+T-C)/(S-T)]時,復制動態回趨于穩定狀態P*2=1,即所有信用評級機構均不為發行機構提供虛高評級服務。
三、博弈參數分析及結論
當P*=(2S-C+T)/(S-T)時,形成的是鷹鴿博弈,令P*=(2S-C+T)/(S-T)=1,則C=S+2T,這表明當S+2T不斷接近C時,不提供虛高評級服務的信用機構的比例將會趨向于 ;當P*=(2S+T-C)/(S-T)時,形成協調博弈,信用評級機構之間的博弈將會演化為兩個穩定狀態,均提供虛高評級服務和均不提供虛高評級服務。當信用評級機構提供虛高評級服務所支付的成本 與信用評級機構不提供虛高評級服務所流失客戶導致的損失C不斷接近時,能夠使提供虛高評級服務的穩定狀態區間不斷縮小。因此,監管部門應加強對信用評級機構的監管和處罰力度。
參考文獻:
[1] 柳永明.美國對信用評級機構的監管:爭論與啟示[J].上海金融,2007(12).
[2] 陳瑩.我國信用評級業監管研究與監管體系構建[J].征信,2010(2).
[3] 秦鳳鳴.信用評級悖論與利益博弈研究綜述[J].經濟學動態,2011(4).
[4] 曹洪軍,陳好孟.不確定環境下我國綠色信貸交易行為的博弈分析[J].金融理論與實踐,2010(2).

