淺議中職數學問題情境的設計

錢國棟

包頭機電工業職業學校

淺議中職數學問題情境的設計

錢國棟

包頭機電工業職業學校

《新課程標準》提倡課程與生活的聯系，倡導在教學過程中合理創設問題情境，幫助學生理解教材內容，激發學生的學習興趣，從而提高教學效率。本人在教學實踐中，特別注重學生的“探究和體驗”。基于這樣的理念，教學中就需要一種學習情境，尤其是最近興起的理實一體化教學更是如此。情境是基于學生固有知識和經驗的，是學生“溫故而知新”的橋梁。本文就自己在中職數學教學中如何從根據學生特點入手，設計問題情境例談體會。

新課程；問題情境；創設方法

一、什么是問題情景？其心理依據是什么？

是指個體面臨的數學問題和它所具有的相關經驗所構成的系統。合適的問題情境，指的是外部問題和內部知識經驗條件的恰當程度的沖突，使其引起最強烈的思考動機和最佳的思維定向的一種情境。

“問題情境”是數學概念賴以產生的現實背景，也一種“氣氛”，能促使學生積極地、主動地、自覺地去思考、想象、探索，去發現規律或著解決問題，并伴隨著積極的情感體驗。

創設問題情境的主要心理依據是“情緒心理學”。研究表明：個體的情感對認知活動至少有動力、強化、調節三方面的功能。“動力功能”指情感對認知活動的增力或減力的效能，即積極的、健康的情感會對人的認知活動起積極的發動和促進作用，而不健康的、消極的負面情緒對認知活動起抑制和阻礙作用。

二、中職數學課堂教學中創設問題情景的原則

創設問題情景在中職數學課堂教學中，必須符合中職數學的學科特點和學生的認知規律。從多年的教學實踐來看，我認為中職數學課堂創設問題情景應遵循以下原則：

1、實用性原則對于中職學生，基礎普遍比較差，更需要切合實際才能引起共鳴，因此就需要精心考慮問題情境的對于學生是否適合、實用。所以，我把這個原則放在第一位。

2、啟發性原則數學教學是需要積極思維的教學活動，若學生不能進行積極思維，那么課堂一定很沉悶。而學生能積極思維，則依賴于教師的精心的點撥和啟發。所以，創設問題情境應以啟發學生思維為立足點。

3、一致性原則即創設問題情境必須與教學內容保持相對一致。

4、科學性原則數學是嚴密、抽象的科學，其表達形式極具規范性。因此，在中職數學課堂創設問題情景，既要照顧學生的接受能力，需要形象、生動、通俗的語言，又不能喪失嚴密準確的特點，切不可為了達到某種課堂效果而信口比喻。

5、靈活性原則“每節課都是新的”，這話無論是學生和老師都是如此。由于學生個性特點不同，堂課的偶發事件也常見，因此教師應根據實際需要靈活創設問題情景，化解課堂問題。

三、創設問題情境的主要方式

從多年實踐經驗看，我把創設問題情景的主要方式歸納為以下幾種：

1、根據學生特點，創設具有趣味性問題情境，激發學生學習的興趣及主動性。例如：在“概率”的教學中，組織學生做摸獎游戲實驗。教師制作帶號乒乓球若干，放入帶孔紙箱，并給學生分配等額的游戲紙幣，總額20“元”。上課時，先通過擲色子得出中一、二、三等及安慰獎號碼，再讓學生分組摸獎，2“元”一次。活動結束后各組通過統計后提問學生：各個數字出現的可能性是否是相等的?不中獎與中獎可能性哪種大?然后在進行一輪，對學生的猜想是進行檢驗。這樣，通過貼近生活的摸獎游戲，使學生體驗“玩中學、學中玩”的學習樂趣，充分調動學生的積極性、主動性，調動思維，活躍課堂氣氛，做到事半功倍課堂效果。

2、創設直觀性圖形情境，引導學生深刻理解數學概念。例如在教授平面的基本性質3時，可以通過實驗，用圖釘、硬紙板，做道具，觀察幾顆圖釘能將硬紙板架起來，這幾枚圖釘排列有何要求（不在一條直線）。

3、創設新異懸念情境，引導學生自主探究。同樣是概率問題，可以這樣設定情境：有儲物柜，每層放有兩個抽屜，僅有一件神秘物體藏在某個柜子中，規定是：只允許打開三層間中的一層并打開其中一個抽屜即為一次游戲，找到神秘物體為游戲勝出，你能一次就獲勝嗎？（如圖）。

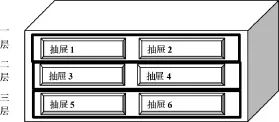
概率方面知識是新課標體系中的重要組成部分，在學生面前用懸疑式的游戲形式，或者采取比賽的形式，可以讓這個探究結果充滿懸念。只要學生能夠接受這種形式，他們就會喜愛并及及參與，從而使教學中的學習任務順利地開展，進而提高學習的效率。通過展示形式多樣、富有理性、充滿懸念的設計和富有有新意的問題情境，使學生在“玩”中學，“趣”中練，“樂”中成長。

4、創設具有應用性的問題情境，引導學生發現數學命題（定理、公式、性質等）。這類問題情境也非常用在理實一體化課程方案中。

例如“集合”教學中，可設計：

校小賣部新進一批貨物：橡皮、小刀、桔子、蘋果、餅干，面包、中性筆，毛巾、香皂等，請把這些物品分類放入陳列架上。

這是一個簡單問題，但是對于學習集合是很典型的，既貼近生活實際，又能給學生創設一個概括、抽象、聯想、數學化的過程。

5、創設開放性問題情境，提高學生思維的品質。

例如在“橢圓及其標準方程”一節的教學中，設置這樣的問題：

中國從“神州5號”到“神舟11號”，實現了中國人的飛天夢想從無到強的巨大轉變。請問：“神州”飛船繞什么旋轉？它的運行軌跡是什么？然后讓學生拿出課前準備好的細繩一段、一塊紙板、兩枚圖釘，按每2人一組根據課本上的要求繪制橢圓，最后概括出橢圓的定義。

當然，只要符合橢圓定義，無論學生畫出什么樣的橢圓，答案都應該認定是正確的。

6、創設疑惑陷阱情境，引導學生主動參與討論，增強防御"陷阱"的經驗。

這類問題往往貌似簡單，而問題通常與我們常見的一些題型類似，如果不加推敲，很容易落入陷阱。就像一些“腦筋急轉彎”一樣。我們可以通過對易錯問題的辨析，不僅能使學生從“陷阱”中跳出來，增強了防御“陷阱”的能力，同時使學生參與討論，自覺的辨析正誤，培養學生的思維嚴密性。

[1]數學課程標準解讀.北京師范大學出版社

[2]吳響鈴.重視數學實驗教學對學生的影響.基礎教育課程，2011(5):57-58

[3]羅增儒.中學數學課例分析.陜西師范大學出版社2003.2

錢國棟（1974-），男，滿族，內蒙古包頭人，本科，講師，研究方向：數學。