初中數學解題思路探析

江西省宜春市澡溪學校 胡 娟

初中數學解題思路探析

江西省宜春市澡溪學校 胡 娟

初中數學是一門重要的學科，其涵蓋了三角函數、代數以及幾何等多方面內容。而這些基礎知識不但能夠將學生的數學學習情況反映出來，而且還會對其今后更深層次知識的學習產生一定影響。所以，初中數學教師應當結合學生實際學習情況，根據理論基礎知識去建立起有效的初中數學解決思路，讓學生能夠更輕松地學習初中數學知識，從而促進初中數學教學質量的有效提升。為此，下文就初中數學解題思路進行簡要分析。

一、對稱性解題思路

對稱性解題思路指的是根據對稱原理，運用形象或抽象思維來構建起具有對稱特征的幾何圖形、數學模型以及代數表達式。如“等腰三角形的兩個底角相等”、“圓的直徑能夠平分圓”等，并且在初中數學題目中也存在著許多類型的對稱，如對稱方程式、對稱不等式、中心對稱圖形、軸對稱圖形等，部分數學題目中還隱含著對稱的條件，所以在解決和對稱相關的數學題時，可以有效應用對稱性解題思路來進行解題，以簡化解題步驟，提高解題效率。

例1 已知0＜a＜1，0＜b＜1，0＜c＜1，求證abc（1-a）（1-b）（1-c）≤（ ）3。

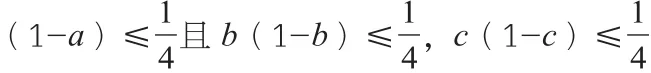
證明：∵題目已知0＜a＜1，

二、數形結合解題思路

數形結合是初中數學最為常用的解題思路之一，尤其是在進行函數解題時，我們不難發現函數變量與圖形間是一個相輔相成的關系，在函數變量中隱含有圖像資料，而圖像又能夠將函數的變量關系反映出來。……