也談錯(cuò)誤資源的分析與利用

潘紅娟

【摘要】學(xué)生學(xué)習(xí)過(guò)程中的錯(cuò)誤，應(yīng)該是重要的教學(xué)資源。在“捕捉錯(cuò)誤，分析錯(cuò)誤，利用錯(cuò)誤”這一基本錯(cuò)誤觀的基礎(chǔ)上，本文以課例為載體，用例析的方式，從“怎樣的錯(cuò)誤信息是典型材料”“哪些維度分析錯(cuò)誤成因”“如何多角度利用與轉(zhuǎn)化”等視角，提出“重錯(cuò)誤的預(yù)設(shè)與展開(kāi)”“重錯(cuò)誤的歸因與分析”“重錯(cuò)誤的多角度利用”等觀點(diǎn)。

【關(guān)鍵詞】小學(xué)數(shù)學(xué) 錯(cuò)誤 分析 利用

教師作為學(xué)生學(xué)習(xí)的促進(jìn)者，其教學(xué)決策是根據(jù)對(duì)學(xué)生的已有知識(shí)、思維水平的了解而展開(kāi)的。因此，唯有讀懂學(xué)生，才能有針對(duì)地實(shí)施教學(xué)，而關(guān)注并讀懂學(xué)生的錯(cuò)誤，應(yīng)該是讀懂學(xué)生的重要方面。

當(dāng)前，“錯(cuò)誤是重要的學(xué)習(xí)資源”“暴露錯(cuò)誤、捕捉錯(cuò)誤、分析錯(cuò)誤、利用錯(cuò)誤，促進(jìn)有效教學(xué)”等理念已成為教師們的共識(shí)。那么，當(dāng)“錯(cuò)誤觀”“資源觀”已被大多教師接受并付諸行動(dòng)的時(shí)候，還有什么是值得討論的呢？筆者認(rèn)為，如何精選材料呈現(xiàn)典型錯(cuò)誤？如何進(jìn)行錯(cuò)誤的歸因分析？如何實(shí)現(xiàn)錯(cuò)誤資源的有效利用？從哪些視角進(jìn)行錯(cuò)誤利用？可能是可以進(jìn)一步探討的話題。

一、什么材料有利于呈現(xiàn)典型——重錯(cuò)誤的預(yù)設(shè)與展開(kāi)

學(xué)生呈現(xiàn)的錯(cuò)誤往往是多姿百態(tài)、極具個(gè)性的，如何從大量信息中呈現(xiàn)最為典型的信息作為教學(xué)資源展開(kāi)？怎樣的錯(cuò)誤直指知識(shí)內(nèi)核？怎樣的錯(cuò)誤凸顯核心目標(biāo)？以“乘法運(yùn)算定律的練習(xí)”一課作為例子闡述如下：

教師呈現(xiàn)下列材料與任務(wù)：

用你認(rèn)為最好的方法計(jì)算下面各題：

（1）96×25 （2）39×99+99

（3）98+2×132 （4）56×720+28×560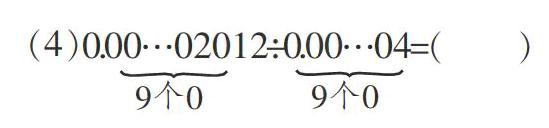

教師搜集并呈現(xiàn)學(xué)生作業(yè)：

生1：96×25=（24×4）×25=24×25+4×25。

生2：39×99+99=39×100。

生3：98+2×132=100×132。

生4：56×720+28×560=40320+15680。

不難發(fā)現(xiàn)，這些錯(cuò)誤，是學(xué)生學(xué)完“乘法運(yùn)算定律”進(jìn)行簡(jiǎn)算時(shí)出現(xiàn)的典型情況。題（1），將“96×25”分解為“（24×4）×25”后，形似的結(jié)構(gòu)導(dǎo)致學(xué)生將“乘法結(jié)合律”與“乘法分類(lèi)律”進(jìn)行混淆。題（2），貌似“39×99+39”的題目類(lèi)型導(dǎo)致學(xué)生慣性地轉(zhuǎn)化為“39×100”。題（3），“湊整簡(jiǎn)算”的功利驅(qū)動(dòng)，使學(xué)生忽視運(yùn)算定律與運(yùn)算順序的正確運(yùn)用。題（4），缺乏轉(zhuǎn)化經(jīng)驗(yàn)，不能靈活運(yùn)用轉(zhuǎn)化策略。我們來(lái)看，教師又是如何利用這些生成資源展開(kāi)，關(guān)注“運(yùn)算定律的再理解”“簡(jiǎn)算方法的再鞏固”“簡(jiǎn)算策略的再體驗(yàn)”，從而凸顯本節(jié)課的核心目標(biāo)的呢？

反饋交流：

生1：不可以用乘法分配律，96×25=（24×4）×25應(yīng)該等于24×（4×25）=2400，這是運(yùn)用了乘法結(jié)合律。（24+4）×25才能等于24×25+4×25。

生2：39×99+99應(yīng)該等于40×99，因?yàn)?9個(gè)99加上1個(gè)99等于40個(gè)99。如果是39×99+39，才等于39×100。

生3：第（3）題，98+2×132不能簡(jiǎn)便計(jì)算，如果是98×132+2×132才等于100132。

師：這一題真的不能簡(jiǎn)便嗎？

生：可以簡(jiǎn)便的，把98+2×132轉(zhuǎn)化成100+2×131，計(jì)算就很方便了。

師：為什么可以這樣算？

生1：把98看作100，多加了2，后面減少1個(gè)2，就變成了100+2×131。

生2：56×720+28×560其實(shí)可以轉(zhuǎn)化成“560×72+28×560”，就等于“560×（72+28）=560×100”了。

生3：還可以轉(zhuǎn)化成“56×720+56×280=56×（720+280）=56×1000”。

生4：還可以轉(zhuǎn)化成28×580+28×1440。

師：這些方法，通過(guò)轉(zhuǎn)化都可以用乘法分配律進(jìn)行簡(jiǎn)便計(jì)算，但這些方法同樣簡(jiǎn)便嗎？

生：轉(zhuǎn)化成“28×580+28×1440”比前兩種方法容易錯(cuò)，如果有很多方法，一般我們選簡(jiǎn)單不容易錯(cuò)的方法。

隨著錯(cuò)誤的呈現(xiàn)，教師引導(dǎo)學(xué)生充分交流、評(píng)價(jià)分析，有效促進(jìn)了“一題多目標(biāo)”的巧妙實(shí)現(xiàn)。“乘法結(jié)合律和乘法分配律的概念辨析”“乘法分配律要關(guān)注相同因數(shù)”“計(jì)算時(shí)要突破思維定勢(shì)”“加減法簡(jiǎn)便運(yùn)算的綜合運(yùn)用”“運(yùn)用轉(zhuǎn)化使計(jì)算簡(jiǎn)便”“方法策略可以多樣”“策略的最優(yōu)選擇”等目標(biāo)隨之實(shí)現(xiàn)。四道算式，能達(dá)成多元目標(biāo)，其背后是有“的”放矢，精選錯(cuò)誤材料，是最為關(guān)鍵的策略。有的放矢的前提是教師對(duì)學(xué)生學(xué)習(xí)心理、學(xué)習(xí)錯(cuò)誤的研究。

二、為什么會(huì)有這樣的錯(cuò)誤——重錯(cuò)誤的歸因與分析

對(duì)待錯(cuò)誤，進(jìn)行有效歸因分析，應(yīng)該是我們了解錯(cuò)誤原因、改進(jìn)教學(xué)的前提。一般，歸因分析可從教材、教師、學(xué)生三個(gè)維度進(jìn)行。對(duì)教材的審視，可以從教材的難度、體系、跳躍性等方面進(jìn)行審視；教師的教學(xué)反思，可以從教學(xué)理念、教學(xué)目標(biāo)、教學(xué)方法、教學(xué)過(guò)程等方面進(jìn)行思考；對(duì)學(xué)生學(xué)習(xí)的診斷，則可從學(xué)習(xí)基礎(chǔ)、學(xué)習(xí)能力、學(xué)習(xí)習(xí)慣、學(xué)習(xí)心理等方面進(jìn)行。

以五年級(jí)的小數(shù)除法為例，對(duì)下面題目進(jìn)行作業(yè)情況統(tǒng)計(jì)與分析。

（1）7.8÷0.75

（2）①0.42÷3.5 ②0.35×0.16

（3）0.78+0.22÷5

1.以教材角度審視

題（1），7.8÷0.75，正確率僅為80.6%，較之于正確率基本在98%以上的其他小數(shù)乘除筆算，顯然偏低。學(xué)生典型錯(cuò)解為“7.8÷0.75=1.4”。探究原因，教材編排缺失、缺少相應(yīng)例題、鞏固練習(xí)不夠，應(yīng)該是主要原因。這是一道商中間有0的除法。在人教版四年級(jí)教材中，沒(méi)有出現(xiàn)“商中間有0”的除法。而在五年級(jí)教材中，僅有四道此類(lèi)習(xí)題。教材編寫(xiě)可能出于減低難度、減少訓(xùn)練的考慮，但教材的跳躍，缺乏對(duì)商中間有0的除法的算理理解與算法鞏固，致使基礎(chǔ)知識(shí)與基本技能的掌握出現(xiàn)問(wèn)題，這就需要教師在教學(xué)時(shí)做相應(yīng)的補(bǔ)充與完善。

2.以教師角度反思

題（2），①0.42÷3.5 ②0.35×0.16，由于沒(méi)有明確的簡(jiǎn)算提示，大多學(xué)生用筆算解決。經(jīng)統(tǒng)計(jì)，①0.42÷3.5，僅1.2%的學(xué)生簡(jiǎn)算，方法為：0.42÷7÷0.5；題②0.35×0.16，僅1.5%的學(xué)生簡(jiǎn)算，方法為：0.35×2×0.08，（0.35×2）×（0.16÷2），0.07×（5×0.16），0.35×0.4×0.4。由此可見(jiàn)，運(yùn)算能力中“自覺(jué)主動(dòng)進(jìn)行靈活計(jì)算的意識(shí)培養(yǎng)”仍然還是水中花、鏡中月，值得關(guān)注。究其原因，是由于教師對(duì)計(jì)算教學(xué)的目標(biāo)視野較為狹窄與單一，對(duì)“運(yùn)算能力”這一核心概念的理解不深刻，以致日常教學(xué)中缺乏靈活計(jì)算的意識(shí)培養(yǎng)與策略積累。

3.以學(xué)生角度診斷

題（3），正確率為83.3%，學(xué)生的典型錯(cuò)誤為：“0.78+0.22÷5=1÷5=0.2”“0.22÷5=0.44”。第（4）題，正確率為45.4%，典型錯(cuò)誤是將算式轉(zhuǎn)化為2012÷4=503。顯然，一方面反映學(xué)生的審題習(xí)慣缺失，學(xué)生按照思維慣性、隨意計(jì)算，導(dǎo)致計(jì)算錯(cuò)誤。另一方面，也反映學(xué)生對(duì)于小數(shù)除法的計(jì)算方法理解不深，無(wú)法將計(jì)算原理與計(jì)算法則運(yùn)用于較為復(fù)雜的計(jì)算情境中。小數(shù)除法計(jì)算方法的本質(zhì)是“將除數(shù)是小數(shù)的除法轉(zhuǎn)化成除數(shù)是整數(shù)”，此題可轉(zhuǎn)化為2.012÷4，而學(xué)生面對(duì)此問(wèn)題，已忽略了筆算除法的基本方法，從而出現(xiàn)隨意轉(zhuǎn)化或無(wú)從下手的情況。

三、怎樣有效利用錯(cuò)誤展開(kāi)教學(xué)——重錯(cuò)誤的多角度利用

錯(cuò)誤搜集與整理的途徑，一般可以通過(guò)作業(yè)、測(cè)查等進(jìn)行統(tǒng)計(jì)分析，也可以在教學(xué)過(guò)程中隨機(jī)觀察捕捉。錯(cuò)誤，根據(jù)其可預(yù)料性，可以分為預(yù)設(shè)性錯(cuò)誤和生成性錯(cuò)誤。如何運(yùn)用這些資源，關(guān)注學(xué)生的困難，在難點(diǎn)處展開(kāi)，從而達(dá)成核心目標(biāo)，這就需要教師敏銳洞察、篩選捕捉、有效利用。

1.利用錯(cuò)誤，掌握基本方法

基本知識(shí)、基本技能的探索階段，我們一般會(huì)讓學(xué)生進(jìn)行嘗試探究，此時(shí)，學(xué)生根據(jù)已有的知識(shí)經(jīng)驗(yàn)，必然會(huì)有試誤的過(guò)程，這就需要教師及時(shí)組織學(xué)生進(jìn)行比較、評(píng)價(jià)、交流，實(shí)現(xiàn)對(duì)基本方法的理解與掌握。

五年級(jí)上冊(cè)根據(jù)實(shí)際需要用“進(jìn)一法”和“去尾法”取商的近似值一課，例題是：小強(qiáng)的媽媽要將2.5kg香油分裝在一些玻璃瓶里，每個(gè)瓶最多可裝0.4kg，需要準(zhǔn)備幾個(gè)瓶？

教學(xué)中，教師采用的基本策略是：經(jīng)歷“利用經(jīng)驗(yàn)嘗試解決問(wèn)題——搜集捕捉學(xué)生資源——有序呈現(xiàn)充分討論”的過(guò)程。引導(dǎo)學(xué)生分析問(wèn)題、嘗試解決，出現(xiàn)以下方法：

生1：2.5÷0.4=6（個(gè)）……0.1（千克），需要6個(gè)。

生2：2.5÷0.4=6.25≈6（個(gè)），四舍五入，需要6個(gè)。

生3：2.5÷0.4=6.25（個(gè)），瓶子要整數(shù)個(gè)， 6+1=7（個(gè)）。

生4：2.5÷0.4=6……0.25（個(gè)），還有0.25個(gè)沒(méi)法放，6+1=7（個(gè)）。

生5：2.5÷0.4=6.25≈7（個(gè)）。

教師將學(xué)生解決的思路一一呈現(xiàn)，通過(guò)集體交流討論，充分肯定合理的成分，最后優(yōu)化得出一般的方法，即商用小數(shù)表示，用“進(jìn)一法”求近似值。這一過(guò)程中，教師搜集了最為豐富的生成性資源，呈現(xiàn)不同的思維成果，最終幫助學(xué)生形成基本方法。

2.利用錯(cuò)誤，凸顯本質(zhì)特征

一般我們會(huì)采用概念辨析的方法，幫助學(xué)生理解概念的本質(zhì)，如何運(yùn)用錯(cuò)誤，凸顯概念內(nèi)涵，拓寬概念外延？也是值得我們思考的。

例如，“長(zhǎng)方體正方體的體積練習(xí)課”中，“柱體”概念的建立完善教學(xué)。

首先，教師由長(zhǎng)方體體積公式復(fù)習(xí)，引出柱體體積公式。

師：這是一個(gè)長(zhǎng)方形和正方形，將它們分別向前、向后平移4cm，得到什么圖形？請(qǐng)求出它們的體積。

師：體積=長(zhǎng)×寬×高，同樣的一個(gè)算式，還可以怎理解？（底面積×高），這樣的圖形也可以叫作柱體。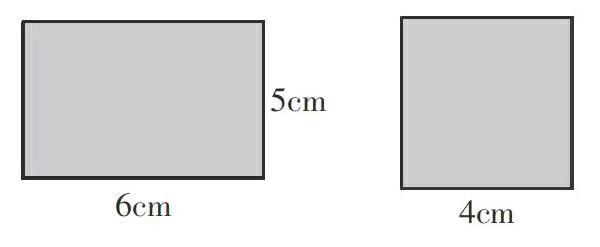

師：除了“6×4表示底面積，5表示高”外，其他面可以作為底嗎？高又是多少？正方體的體積，可以表示成“底面積×高”嗎？底面積是多少？高是多少？

師：什么情況下，我們可以用“底面積×高”來(lái)計(jì)算體積？

出示：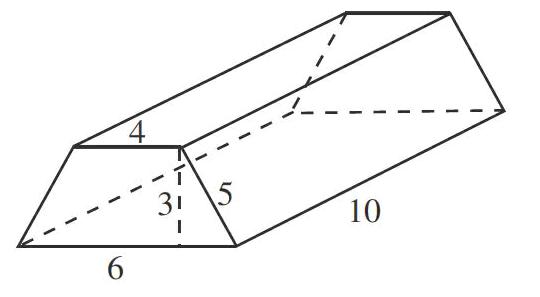

師：這是柱體嗎？請(qǐng)求出它的體積，只列式不計(jì)算。

根據(jù)學(xué)生作業(yè)情況呈現(xiàn)兩種方法：

生1：（6+4）×3÷2×10。

生2：6×10×3。

師：把下面的長(zhǎng)方形“6×10”看作底面，“3”作為它的高，可以嗎？

生1：不可以，柱體底面應(yīng)該是指每個(gè)面都相等的面，如果將底面向上平移應(yīng)該每個(gè)面都一樣。如果將“6×10”這個(gè)面往上平移，并沒(méi)有和上底面重合。

生2：柱體的高應(yīng)該處處相等，只有將側(cè)面的梯形看作底面，高都是10。

師根據(jù)學(xué)生回答隨機(jī)課件演示：

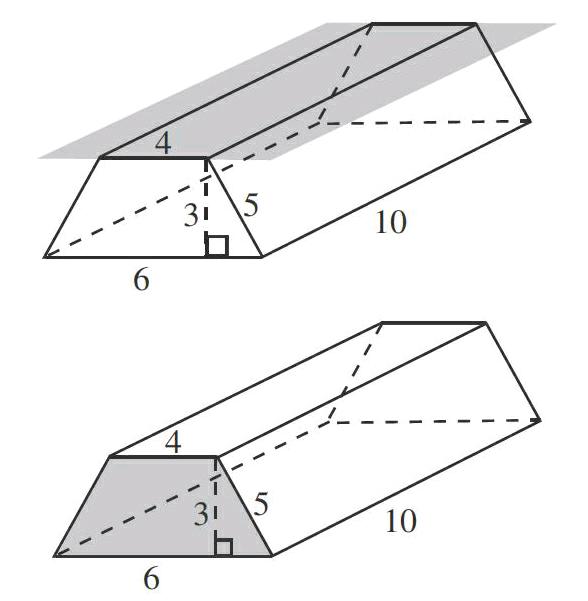
這一片段中，教師及時(shí)捕捉“6×10×3”這一錯(cuò)誤資源，進(jìn)行放大處理，運(yùn)用概念辨析、直觀演示，很好揭示了柱體“上下底面相等”“與底面平行的任何一個(gè)截面都相等”“高處處相等”等特征。

3.利用錯(cuò)誤，形成反思意識(shí)

錯(cuò)誤才有反思的價(jià)值，如何運(yùn)用學(xué)生錯(cuò)誤，幫助學(xué)生在鞏固技能的同時(shí)，形成及時(shí)反思、回顧檢驗(yàn)的意識(shí)與習(xí)慣，體驗(yàn)反思檢驗(yàn)的多樣方法呢？

例如：“小數(shù)乘除法練習(xí)課”一課。

豎式計(jì)算：0.75×0.15，380×2.6，

4.872÷0.24。

教師隨機(jī)選擇學(xué)生作業(yè)，重點(diǎn)反饋：

（1）0.75×0.15=11.23；（2）380×2.6=98.8；（3）4.872÷0.24=2.03。

師：這些同學(xué)的計(jì)算正確嗎？有什么辦法判斷是錯(cuò)誤的？這樣的方法你能找到多少種？

生1：可以從小數(shù)位數(shù)看，0.75×0.15是四位小數(shù)，而這個(gè)同學(xué)的結(jié)果是兩位小數(shù)。

生2：末尾應(yīng)該是5，而不應(yīng)該是3，所以這個(gè)結(jié)果一定是錯(cuò)的。

生3：因數(shù)乘以一個(gè)比1小的數(shù)，結(jié)果一定比這個(gè)因數(shù)小，0.75×0.15<0.75，11.23比0.75大了，結(jié)果一定錯(cuò)了。

師：用同樣的方法能判斷第2題嗎？

生4：380×2.6=98.8，還可以用估算的方法判斷，380乘以2點(diǎn)多，積最少應(yīng)該有760多，而這個(gè)結(jié)果是98.8，一定不對(duì)。

生5：a×b（b>1），積>a。380×2.6=98.8，結(jié)果比380小了。

生6：4.872÷0.24=2.03，這一題可以用乘法檢驗(yàn)，2.03×0.24≠4.872，因?yàn)?.03×0.24的結(jié)果比2.03小，不可能等于4.872。

生7：同樣可以估算，4.872÷0.24=487.2÷24，大約等于20多。

師：是的，我們?cè)谒愠鼋Y(jié)果后，一般要進(jìn)行回顧檢驗(yàn)，剛才同學(xué)們用到了很多方法，都可以作為今后進(jìn)行檢驗(yàn)的策略。

這一片段中，錯(cuò)誤資源巧妙地轉(zhuǎn)化為“反思意識(shí)滲透”“檢驗(yàn)方法落實(shí)”的載體。錯(cuò)誤處理片段中，“根據(jù)位數(shù)判斷”“根據(jù)尾數(shù)檢驗(yàn)”“根據(jù)積與因數(shù)的大小關(guān)系”“運(yùn)用估算檢驗(yàn)”“互逆驗(yàn)算”等方法在錯(cuò)誤評(píng)價(jià)中得以有效滲透與落實(shí)。

4.利用錯(cuò)誤，體會(huì)數(shù)學(xué)思想

學(xué)生生成資源的智慧運(yùn)用，對(duì)易錯(cuò)易混知識(shí)的澄清、概念本質(zhì)的理解、方法技能的落實(shí)等，都能起到積極的作用。同樣，利用生成材料，將錯(cuò)誤提升為更高層面的解決策略，在體會(huì)數(shù)學(xué)思想方法方面也會(huì)起到意想不到的效果。

例如：“三角形的面積練習(xí)”一課。

材料：點(diǎn)E、F、G、H分別在長(zhǎng)方形ABCD的四條邊上，求四邊形EFGH的面積。（單位：cm）

1.任務(wù)：選擇條件，想辦法求出四邊形EFGH的面積。

2.學(xué)生嘗試，教師巡視，選擇典型，方法討論。

生1：用總面積減去空白部分四個(gè)小三角形的面積。

生2：連接EG，分別求出兩個(gè)三角形EFG和EGH的面積，這兩個(gè)三角形底都是4cm，所以面積是（3+7）×4÷2=20cm2。

生3：也可以連接FG，上下兩個(gè)三角形，EFH的面積加上FGH的面積也是可以的。

生4：這是錯(cuò)的，這兩個(gè)三角形的底和高都不知道，沒(méi)辦法求的。

師抓住這種方法，引導(dǎo)提問(wèn)：這個(gè)同學(xué)想要將上下兩個(gè)三角形的面積加起來(lái)，想法很好，有辦法使它們面積不變，但可以相加嗎？

此時(shí)，教室里十分安靜，突然，有學(xué)生舉手。

生5：如果將H點(diǎn)往下移動(dòng)一點(diǎn)，使FH和AD平行，那么，這兩個(gè)三角形的底都是10，高都是2，就能求出面積了。

師：這個(gè)同學(xué)想到運(yùn)用轉(zhuǎn)化，將EGH轉(zhuǎn)化為面積相等的三角形EGH′，就可以解決了（如圖1）。為什么可以這樣？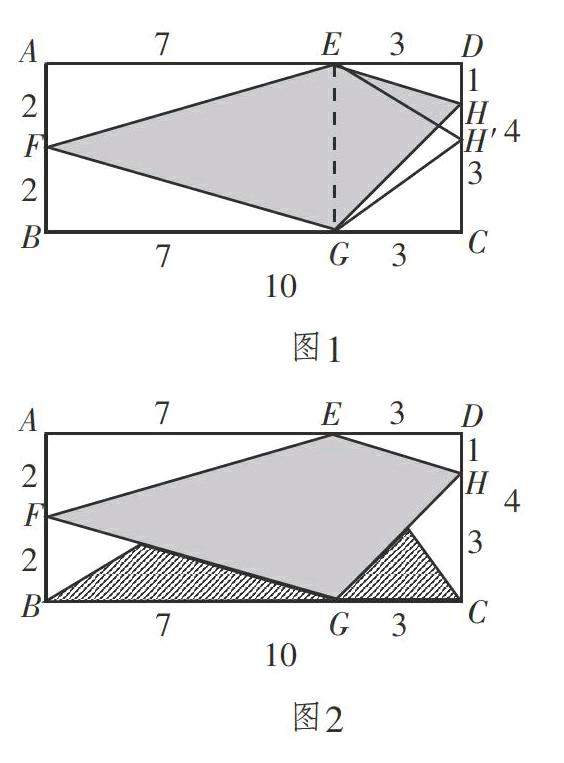

生5：因?yàn)镋GH和EGH′底都是EG，而且平行線之間的距離相等高就相等，面積就一定相等。

生6：如果可以移動(dòng)的話，把F、H分別移動(dòng)到最下面，和B點(diǎn)、C點(diǎn)重合，就可以把原來(lái)的四邊形EFGH轉(zhuǎn)化成一個(gè)三角形EBC。這個(gè)三角形的底是10cm，高是4cm，面積是10×4÷2=20cm2，如圖2。

這一片段中，“上下兩個(gè)三角形EFH加上FHG的面積”這一錯(cuò)誤方法，成為教師激活“等積變形”“轉(zhuǎn)化思想”的有利時(shí)機(jī)，促發(fā)了“讓靜止的圖形動(dòng)起來(lái)”的策略意識(shí)，學(xué)生不僅感受了“轉(zhuǎn)化”的作用，并很好積累了運(yùn)用轉(zhuǎn)化解決問(wèn)題的經(jīng)驗(yàn)。這個(gè)片段中，無(wú)疑，錯(cuò)誤的捕捉與轉(zhuǎn)化是極為巧妙而高明的。

【參考文獻(xiàn)】

[1]任景業(yè)著.分享孩子的智慧——改進(jìn)教學(xué)的建議，東北師范大學(xué)出版社.2014.6

[2]蔡金法、許世紅.教師讀懂學(xué)生什么：認(rèn)知導(dǎo)向的教學(xué)，小學(xué)教學(xué).2013年18期