對(duì)一道課本例題的變式探究

安徽省寧國(guó)中學(xué) (242300)

陳曉明

對(duì)一道課本例題的變式探究

安徽省寧國(guó)中學(xué) (242300)

陳曉明

普通高中課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書《數(shù)學(xué)》選修2-1(人教A版)第70頁(yè)例5：過(guò)拋物線焦點(diǎn)F的直線交拋物線于A，B兩點(diǎn)，通過(guò)點(diǎn)A和拋物線頂點(diǎn)的直線交拋物線的準(zhǔn)線于點(diǎn)D，求證：直線DB平行于拋物線的對(duì)稱軸.

圖1

在過(guò)去的教學(xué)中筆者直接講解此例，發(fā)現(xiàn)絕大多數(shù)學(xué)生難以掌握，春去秋來(lái)，又是一屆學(xué)生，我改變了教學(xué)方式.首先將此例具體化為特殊的拋物線y2=4x進(jìn)行研究，然后推向一般即得例題結(jié)論，再進(jìn)一步進(jìn)行變式探究.收到了意想不到的效果！

改編例題：過(guò)拋物線y2=4x焦點(diǎn)F的直線交拋物線于A(x1,y1)，B(x2,y2)兩點(diǎn)，通過(guò)點(diǎn)A和拋物線頂點(diǎn)的直線交拋物線的準(zhǔn)線于點(diǎn)D，求證：直線BD∥x軸.

(為了證明此例，首先給出引例：過(guò)拋物線y2=2px焦點(diǎn)F的直線交拋物線于A(x1,y1)，B(x2,y2)兩點(diǎn)，求證：y1y2=-p2.

課本中的證法有些繁，我給出改編例題的簡(jiǎn)便證法：

接下來(lái)再讓學(xué)生把結(jié)論推向一般式y(tǒng)2=2px，學(xué)生很快證明了課本例5.我緊接著對(duì)例題進(jìn)行變式，并讓學(xué)生證明，然后把結(jié)論推向一般.

變式1過(guò)拋物線y2=4x焦點(diǎn)F的直線交拋物線于A(x1,y1)，B(x2,y2)兩點(diǎn)，過(guò)B點(diǎn)作x軸平行線交準(zhǔn)線于一點(diǎn)D.求證：A，O，D三點(diǎn)共線.

變式2過(guò)拋物線y2=4x焦點(diǎn)F的直線交拋物線于A(x1,y1)，B(x2,y2)兩點(diǎn)，過(guò)B點(diǎn)作x軸平行線與AO延長(zhǎng)線交于一點(diǎn)D.求證：D點(diǎn)在一條定直線上.

拓展1過(guò)點(diǎn)M(2,0)的直線交拋物線y2=4x于A(x1,y1)，B(x2,y2)兩點(diǎn)，過(guò)點(diǎn)B作x軸平行線與AO延長(zhǎng)線交于一點(diǎn)D.求證：D點(diǎn)在一條定直線上.

圖2

∴xD=-2.即D點(diǎn)在一條定直線x=-2上.

拓展2過(guò)點(diǎn)M(a,0)(a>0)的直線交拋物線y2=4x于A(x1,y1)，B(x2,y2)兩點(diǎn)，過(guò)點(diǎn)B作x軸平行線與AO延長(zhǎng)線交于一點(diǎn)D.求證：D點(diǎn)在一條定直線上.

同理可證定直線為x=-a.

試題鏈接:我們來(lái)看一下2014年江西高考題(文科第20題)：

如圖3，已知拋物線C:x2=4y，過(guò)點(diǎn)M(0,2)任作一直線與C相交于A，B兩點(diǎn)，過(guò)點(diǎn)B作y軸的平行線與直線AO相交于點(diǎn)D(O為坐標(biāo)原點(diǎn)).

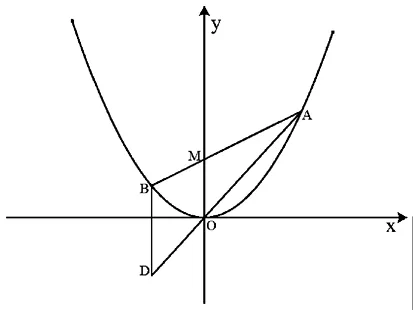
圖3

(1)證明：動(dòng)點(diǎn)D在定直線上；

(2)略.

變式3如圖1，已知D為拋物線y2=4x準(zhǔn)線上一點(diǎn)，拋物線焦點(diǎn)為F，過(guò)D作x軸平行線與拋物線交于一點(diǎn)B(x2,y2)，直線BF與DO延長(zhǎng)線交于一點(diǎn)A(x1,y1)，求證：點(diǎn)A在拋物線上.

變式4如圖1，已知D為拋物線y2=4x準(zhǔn)線上一點(diǎn)，拋物線焦點(diǎn)為F，連結(jié)DO并延長(zhǎng)與拋物線交于一點(diǎn)A(x1,y1)，過(guò)點(diǎn)D作x軸平行線與直線AF交于一點(diǎn)B(x2,y2).求證：點(diǎn)B在拋物線上.

證明略.

變式5如圖1，已知D為拋物線y2=4x準(zhǔn)線上一點(diǎn)，拋物線焦點(diǎn)為F，連結(jié)DO并延長(zhǎng)與拋物線交于一點(diǎn)A(x1,y1)，過(guò)點(diǎn)D作x軸平行線與拋物線交于一點(diǎn)B(x2,y2).求證：A，F(xiàn)，B三點(diǎn)共線.

證明略.

反思與小結(jié)

1.條件與結(jié)論共6個(gè)：點(diǎn)A在拋物線上；點(diǎn)B在拋物線上；點(diǎn)D在拋物線準(zhǔn)線上；A，O，D三點(diǎn)共線；A，F(xiàn)，B三點(diǎn)共線；直線BD∥x軸.它們之間有怎樣的關(guān)系？通過(guò)變式探究，我們應(yīng)該有所感悟！

2.這里只對(duì)變式2進(jìn)行了拓展，顯然其它變式同樣可進(jìn)行類似拓展.

3.各種變式中y2=4x易推廣到y(tǒng)2=2px，讓學(xué)生自己完成.

4.拋物線的焦點(diǎn)弦的性質(zhì)非常多，讓學(xué)生課后再去探究.

教學(xué)啟示

1.正如美國(guó)著名數(shù)學(xué)教育家波利亞所說(shuō)：“一個(gè)專心的認(rèn)真?zhèn)湔n的老師能夠拿出一個(gè)有意義的但又不太復(fù)雜的題目，去幫助學(xué)生挖掘問(wèn)題的各個(gè)方面，使得通過(guò)這道題，就像通過(guò)一道門戶，把學(xué)生引入一個(gè)完整的理論領(lǐng)域”.[1]教師要研究教學(xué)，將課本上數(shù)學(xué)知識(shí)的學(xué)術(shù)形態(tài)轉(zhuǎn)化為教育形態(tài)，讓“冰冷的美麗”引起學(xué)生“火熱的思考”.

2.縱觀幾十年的高考試題，信手可得到許多高考試題也來(lái)源于課本教材.教材中的例題習(xí)題具有典型性，示范性，同時(shí)也滲透著一些數(shù)學(xué)思想方法或提供某些結(jié)論.[2]因此，以本為本，重視對(duì)教材中的例題習(xí)題的深入探究，發(fā)現(xiàn)新的東西，是提高高考復(fù)習(xí)效率的最佳捷徑.

[1]于世章.挖掘課本習(xí)題價(jià)值上好復(fù)習(xí)課[J].數(shù)學(xué)通報(bào)，2014(12)：36.

[2]劉飛.2014年高考數(shù)學(xué)安徽卷理科第16題的探究[J].中學(xué)數(shù)學(xué)教學(xué)，2014，(4)：43.