例說幾何畫板在數學探究中的應用
江西省永豐中學 (331500) 劉 忠 呂永斌
例說幾何畫板在數學探究中的應用
江西省永豐中學 (331500) 劉 忠 呂永斌
數學探究是通過觀察、分析數學事實,提出有價值的數學問題,猜測、探求適當的數學結論或規律,并給出解釋或證明的過程.在實際探究中,對于要利用復雜函數圖像的問題,如果靠傳統的方法幾乎是不可能的,而利用幾何畫板的動態數據更新與動態圖形變換功能則能使探究變得簡單輕松、直觀形象.
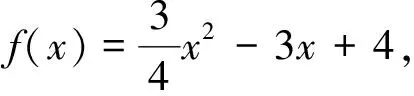
一、文[1]關于問題2的解法展示
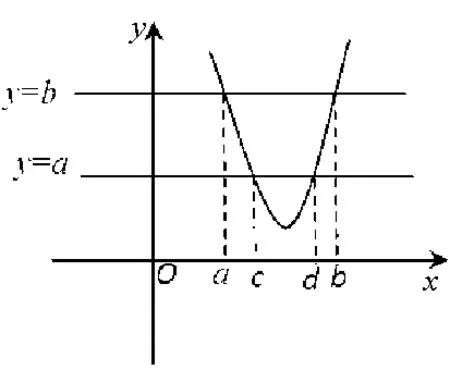
圖1
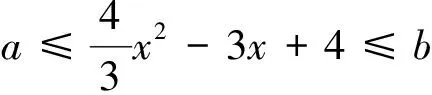
二、并非任意的y=ax2+bx+c(a>0)問題2都有解
如圖2所示,在同一坐標系中分別作出y=ax2+bx+c(a>0)和y=x的圖像,設其一交點(假設有)為A,過A作y軸的垂線交拋物線于點B,再過B作x軸的垂線交直線y=x于點C,從而得到正方形ABCD.因此,只有當拋物線的頂點在正方形ABCD的邊CD上或在正方形ABCD的內部時,問題2才有解.
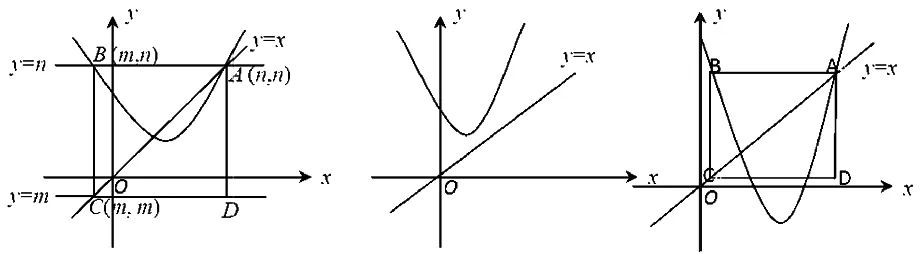
圖2 圖3 圖4
顯然,此處正方形ABCD的作法與文[1]所述“直線y=m過拋物線的頂點或在拋物線下方”是一致的(因為只要滿足“直線y=m過拋物線的頂點或在拋物線下方”,也就滿足了“拋物線的頂點在正方形ABCD的邊CD上或在正方形ABCD的內部),因此“直線y=m過拋物線的頂點或在拋物線下方”是問題2有解的一個必要條件,并不是充要條件.實際上,當拋物線與直線不相交(如圖3所示)或當拋物線的頂點在如前所述的正方形外(如圖4所示)時,問題2就無解了.
三、當a,b,c滿足什么條件時,問題2才有解
以上方法得到了關于問題2是否有解的粗略判斷,所謂“形少數時難入微”,要得到問題2有解時a,b,c的關系,還得從“數”的角度考慮.
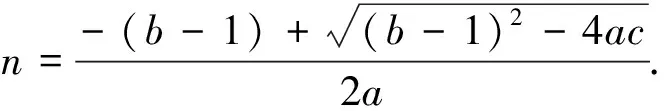
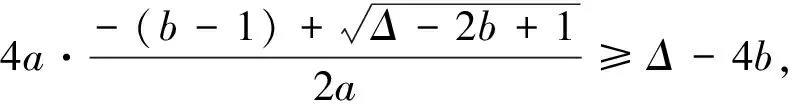
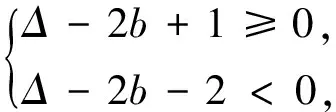
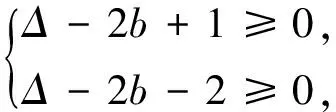
綜(1)(2)所述,對于y=ax2+bx+c(a>0),當a,b,c滿足-1≤Δ-2b<2,或2≤Δ-2b≤8,即-1≤Δ-2b≤8的條件時,“m≤ax2+bx+c≤n的解集恰為[m,n]”才有解.
因此,當a,b,c滿足-1≤Δ-2b≤8的條件時,問題2才有解.
四、用幾何畫板驗證結論
1、利用幾何畫板作出前圖2,步驟如下:
(1)定義坐標系;(2)利用“點”工具,在x軸上取點A,同時選定點A和x軸“構造”“垂線”;(3)在垂線上選取點B,隱藏垂線;(4)利用“射線”工具畫出射線AB;(5)隱藏點B,利用“點”工具在射線上取點C;(6)右鍵點擊點C,得到點C的縱坐標yC;(7)右鍵點擊yC,得到其標簽,命名為a;(8)選取點C,點擊“編輯”“操作類按鈕”“動畫”,然后將“動畫”的“標簽”命名為“點擊此按鈕改變a的值”;(9)隱藏點A、C及射線;(10)利用“點”工具,在x軸上任取點D,E分別構造過此兩點的x軸的垂線j,k;(11)在直線j上利用“點”工具任取點F,并用右鍵得到點F的縱坐標yF;(12)將yF的標簽命名為b;(13)如步驟8,得到“點擊此按鈕改變b的值”;(14)同理,得到“點擊此按鈕改變c的值”;(15)隱藏點D,E,F及直線j,k;(16)點擊“數據”“計算”,由標簽“a,b,c”得到標簽“b2-4ac-2b”;(17)點擊“繪圖”“繪制新函數”利用a,b,c得到函數f(x)=ax2+bx+c及g(x)=x的圖像;(18)通過改變a,b,c將函數f(x)=ax2+bx+c及g(x)=x的圖像調整到有兩交點的情況,并取它們的右交點H;(19)由點H和y軸“構造”垂線l;(20)“構造”垂線l與拋物線的另一交點I;(21)由點I與直線l“構造”垂線m;(22)由直線m與g(x)=x的圖像“構造”交點J;(23)由點J和直線m“構造”垂線n;(24)由點H和直線n“構造”垂線o;(25)由直線n和直線o“構造”交點K;(26)隱藏直線l,m,n,o;(27)構造線段IJ,JK,KH,HI得到正方形IJKH.
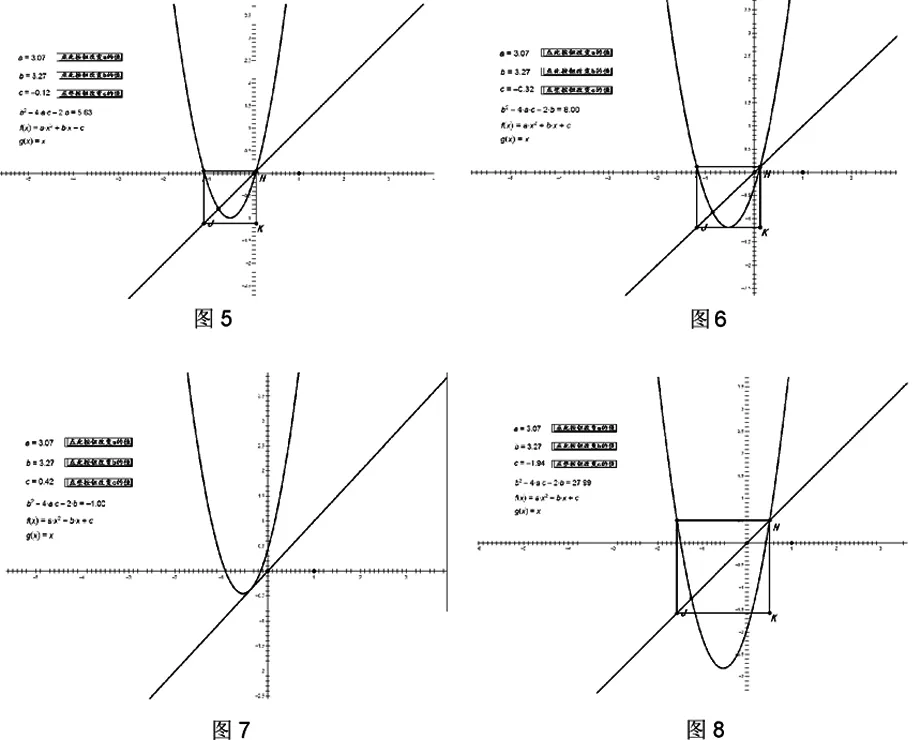
2、通過相關按鈕連續改變a,b,c的值,得到拋物線的頂點與正方形位置關系的所有情況,如圖5-9所示.
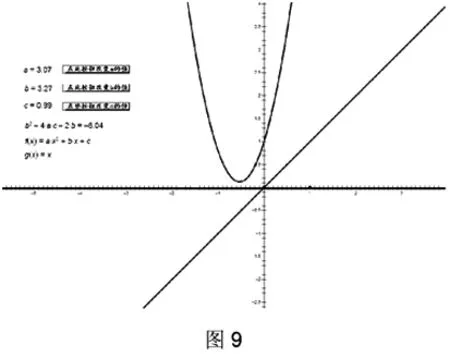
圖9
從圖5中可以看出,當b2-4ac-2b=5.638∈(-1,8)時有解;從圖6、圖7中可以看出,當b2-4ac-2b=8或-1時處于臨界情況也有解;從圖8、圖9中可以看出,當b2-4ac-2b<-1或b2-4ac-2b>8時無解.這樣就驗證了我們所得結論的正確性.
[1]武增明.一對形似質異問題的辨析[J].中學數學教學參考:上旬,2013(10):42-43.
[2]劉 忠.一道值得商榷的形似質異變式題[J].中學數學教學參考:上旬,2016(8):63-64.

