抓住數學本質提升概括能力

李霞

[摘 要]抽象概括將所學數學知識逐層、遞進式串聯，形成有序、完整的數學知識體系，從而為學生鋪設扎實的數學基礎。在教學中，教師應依托典型素材，在概括中探尋規律；借助類型遷移，在概括中拓展思路；強化梳理意識，在概括中強化聯系，從而促進學生數學素養的不斷提升。

[關鍵詞]探尋規律；拓展思路；強化聯系；概括能力

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2017）08-0075-01

概括能力是數學核心素養的重要組成部分。概括的過程是學生提煉和獲取數學知識的過程，也是學生提升數學技能、靈活運用知識、提高綜合素質的重要途徑。正因如此，學生一旦擁有了抽象概括能力，數學這門由易到難階梯上行的學科就不再遙不可及。那么，應如何培養學生的概括能力呢？

一、依托典型素材，在概括中探尋規律

概括是使感性認知上升到理性認知的過程。小學生正處于形象思維向抽象思維的過渡階段，他們的思維在很大程度上仍然以感性認識和實踐操作為主。因此，典型材料是促成學生概括能力生成和發展的重要元素。在教學中，教師要為學生提供與事物本質相關聯的典型材料，并引導他們對典型材料進行深入的感知和理解。

如，學習“分數乘法”后，教師補充了幾組算式練習：先進行計算，并觀察每組的結果，找出規律。

1. -=（ ），×=（ ）；

2. -=（ ），×=（ ）；

3. -=（ ），×=（ ）。

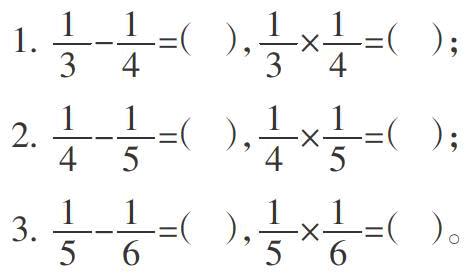
以上每組中的兩個算式雖然不同，但計算結算是相同的。針對這一發現，教師引導學生進行了抽象概括：分母是相鄰的非零自然數，而分子都是1的兩個分數，它們相減和相乘的結果相同。教師追問：“誰能舉出一組有同樣規律的算式？”

學生充分對比觀察題目的核心本質，在發現中探究，在探究中提煉，得出抽象化的結論，隨后教師又從事物的本質屬性出發，引領學生在規律的再運用中獲得充分的感知和體驗。

二、借助類型遷移，在概括中拓展思路

在數學教學中，遷移包括了已掌握的知識與新知識存在的本質聯系，依托本質規律可將已有知識與新知識進行相應的勾連，以及對學生認知結構中的已有知識進行重組。因此，教師要引導學生聯通知識間的內在聯系，關注知識間的本質特征，從而實現數學知識的正遷移。

如，學習“長方體表面積”后，教師出示練習：一個長方體，長和寬都是4厘米，高是8厘米，求這個長方體的表面積？大多數學生都能利用長方體相對面的面積相等的特征，先算出其中3個面的面積，再乘以2就得到長方體的表面積，算式為（4×4+4×8+4×8）×2=160（平方厘米）。也有學生利用底面和頂面相等，且相加等于1個立面，因此只要算出5個立面面積就得到長方體的表面積，算式為4×8×5=160（平方厘米）。還有學生把4個立面分別看成2個底面，又因為底面和頂面相等，那么10個底面面積之和就是這個長方體的表面積，算式為4×4×10=160（平方厘米）。學生借助對長方體概念的理解和遷移，運用多種不同的方法，最終得出相同的答案。

數學知識是一個有機的整體，各部分知識并不是孤立存在的，同樣的問題從不同的視角分析，所得出的方法也不一樣。在實踐應用中，學生將已有認知靈活運用，并在有效重組中優化了數學認知結構，實現了結構重組性遷移。

三、強化梳理意識，在概括中強化聯系

梳理能力是一種數學習慣，更是一種數學素養，它可以幫助學生將所學知識系統化、清晰化。教師應該注重培養學生的梳理意識，為數學核心能力的提升奠基。

如，教學“異分母分數加減法”時，教師出示一道計算題：-。學生對異分母分數的加減法還比較陌生，教師引導學生對所學知識進行了相應的梳理，學生在對知識的回顧中，相機進行了同分母分數相加減的練習和異分母之間的通分訓練。這時教師提示：“既然這兩種題目都會做了，那可不可以運用通分的方法，使計算題中分數的分母相同呢？”新的知識順著教師的有序梳理，已經清晰地展現在學生面前，并串起了通分知識和同分母分數相加減之間的有效聯系。

學生對原有經驗和知識的開發、提煉，是建立在充分理解和真正掌握數學知識、運用數學知識基礎上的，是學生歷練抽象概括能力的重要途徑。

總而言之，在數學學習中，良好的概括能力是學生必須具備的基本素養，是引領學生對所學知識進行歸類、總結、遷移的重要手段。因此，教師在數學教學中應著力培養學生歸納概括的能力，提升梳理知識、總結經驗的意識，從而實現數學教學效率的最大化。

（責編 李琪琦）