挖掘潛能，提高素養，讓初中數學課放飛學生思緒

黃輝

[摘 要] 數學課程重視學生思維能力與解決問題能力的培養. 在初中數學教學中，我們不僅要教知識，更要講方法，在授業的基礎上，挖掘學生的數學潛能，提高他們對數字與空間的敏銳性，潛移默化地培養他們的數學素養. 這樣的素養教學就像一雙隱形的手，雖然看不見，卻扎扎實實地印在學生的成長道路上，真真切切地表現在他們的生活實踐中. 本文主要闡述作者在教學中的幾點實踐.

[關鍵詞] 初中數學；數學素養；思維能力

愛因斯坦曾說過：“當一個學生畢業離開學校時，如果他把這幾年所學的知識忘光了，那么他所剩下的才是學校教育的真正成果. ”這里的“真正成果”，指的是學科知識以外的能力與素養，包括解決問題的思維方式、待人處事的思想品德，還有看待事物的價值觀與人生觀. 這些伴隨學生終生的素養，需要教師在學校教育中悉心栽培，以學生為主體，給予他們思維發散的空間，充分挖掘他們的多維度潛能. 初中數學本身就是一門對邏輯思維要求很高的學科，對學生想象力和創造力的激發有著極大的促進作用. 在初中數學教學中，我們不僅要教知識，恪守“授業”的教學使命，還要講究方法，注重思維能力的培養，幫助學生們由內而外地形成數學思維，提高數學素養. 這比起機械化的教學練習、看似可喜的學習成績更加重要，對學生的知識應用與終生發展起到至關重要的作用. 因此，我們要關注學生數學潛能的發展，重視學生數學素養的提升，讓這群充滿青春活力的學生們在數學教學中放飛思緒，張揚個性. 在如下的教學探索中，筆者從教學理念入手，優化教學方式，引導學生敢于挑戰、重于實際、善于剖析，進而為自己的人生儲備奠定基石.

以生為本，鼓勵學生向未知挑戰

教師自編自導“教案劇”的教學模式已經逐漸退出舞臺，因為“以教師為中心”的“填鴨式”授課方式打擊了學生的積極性，學生僅作為聽眾的“零互動”模式已經無法滿足他們的發展需求. 只有師生平等對話，學生成為課堂的“主體”，才能確保學生有思考的空間，有發言的自由，甚至有挑戰權威的膽識. 以生為本的數學課堂，教師發揮著引導、幫助、激勵和參謀的作用，學生可以憑借自己的理解方式對新知進行自主建構，這一過程確保了學生的主動性. 在這樣的課堂中，教師不再標榜“我說的都是對的”，而是給予了學生反駁教師觀點的機會. 課堂不再“井井有條”，而是多方互動，甚至“適當混亂”. 譬如，數學概念首提，學生分組討論；全新例題列出，學生自主解析；實際問題鏈接，學生多邊延伸……學生就像奧妙宇宙的探索者，一直向思維的更深處前行.

人教版七年級下冊第9章“不等式和不等式組”是一個典型的探究型單元，教學目標從不等式的意義、性質延伸至一元一次不等式組及其運用. 這是學生第一次接觸不等式，學生在課前預習和導入環節表現出既畏懼又好奇的反應. 畏懼來自于未知，好奇則出自對新鮮事物的探秘渴望. 為了激發學生的思維潛能，教師在多媒體設備呈現七年級上冊曾經學習過的“一元一次方程”、七年級下冊學習的“二元一次方程”與今天將要學習的“一元一次不等式”進行對比，學生通過觀察發現三者之間的異同點，并在小組討論中探索出一元一次不等式的結構和特點. 在以往的教學中，教師會列舉眾多一元一次不等式的例題，并重復其概念，待學生理解后再結合練習題進行鞏固. 而在這堂課中，教師首先讓學生自主觀察，再由學生討論得出練習題答案，最后根據學生的反饋幫助他們對不等式進行全面解析. 在解析的過程中，學生可以隨時提出自己的觀點，即用自己的語言去梳理自學與討論后的思路. 比如關于“用一元一次不等式解決問題的步驟”，學生自行總結出五個字“審、設、列、解、答”，并加之以節奏，把這五個字變成解題的小口訣，讀起來朗朗上口，識記起來更加方便，這比起教師羅列的方法更清晰、明了. 可見，在實際教學中，我們要善于發展學生的數學學習潛能，充分發揮他們的想象力與創造力，引導學生自主思考、合作探討，形成具有小組特色、班級特色的學習小策略. 在這樣的自主學習活動中，學生們能夠主動地經歷知識的形成過程，在嘗試與挑戰中，收獲更有意義的數學知識，這對于培養學生的發散思維、拓展學生的數學空間，很有幫助.

從實入手，重視理論向運用過渡

《數學課程標準》指出：“學生的數學學習內容應當是現實的、有意義的、富有挑戰性的，這些內容要有利于學生主動地進行觀察、實驗、猜測、驗證、推理與交流等數學活動. ”數學是一門實用性極強的學科，所有知識來源于生活，也將運用于生活，因此在學習的過程中要引導學生從實際問題出發，建立他們實際解決問題的能力，在學習數學理論的同時學會向生活運用過渡. 這就要求我們在教學的過程中，要善于尋找知識與生活之間的聯系，以學生們熟悉的、身邊的、觸手可及的生活情境、生活問題，創設教學任務，讓學生們在解決生活實際問題的過程中，接觸新知識、學習新知識，把厚重、枯燥、乏味的理論知識變成輕巧而又實用的生活技能，如此一來，數學才能真正有“用”的價值.

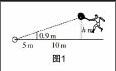
縱觀人教版初中數學教材，單元模塊的設置呈現逐漸由理論延伸至實際運用的趨勢. 譬如我們學習一元一次方程，先學習方程本身，再拓展到用方程解決問題，還有我們學習的普查和抽樣調查，都與我們的生活息息相關. 在九年級下冊第27章“相似”這一單元，我們學習比例的基本性質，了解了線段的比、成比例線段以及圖形的相似，這些理論看似只是邏輯數值與具象圖形的結合，實則生活中有著廣泛的運用. 因此，我們應在課上大范圍列舉實例，比如：如圖1，小明在打網球時，要使球恰好能打過網，而且落在離網5米的位置上， 則球拍擊球的高度h應為（ ）

A. 0.9 m？搖 ？搖？搖 B. 1.8 m

C. 2.7 m？搖？搖？搖 D. 6 m

打網球是學生所喜歡的課外活動之一，這道題目的列舉讓學生興趣滿滿. 另外例題圖形的暗示，讓學生一下子就與“相似三角形”的理論知識關聯起來. 這個問題解決的過程同時也是學生回顧知識的過程，還是抽象理論推向實際問題的關鍵. 為了讓學生更加清晰地感受到理論與實際相結合的力量，教師為學生布置了一個看似不可能完成的任務：測量學校旗桿的高度. 這次教師并未提供圖例輔助學生理解，而學生集思廣益，完成了測量任務，這證明了學生的潛能被激發，并且已經實現了理論向實際的過渡.

以動為先，引導學生用實踐論證

古往今來，每一個偉大數學理論的誕生都離不開科學家的潛心鉆研與實踐論證，這樣偉大的數學精神理應代代相傳. 在以往的教學模式中，當我們在學習數學公式、定律時，總是由教師遵循教材逐一講解，學生再追隨教師的步伐先理解再做題，這樣的形勢下學生思想被動又很難扎實掌握知識精髓，往往在測驗中顯現出短板. 因此，教師應該給予學生更多“動手”的機會，引導他們通過自己的實驗、實踐論證知識點. 因為只有“知其然并知其所以然”，才是內化數學知識并得以提升、運用的基礎.

譬如人教版八年級下冊第17章“勾股定理”的學習中，學生已掌握勾股定理的概念，而關于其運用的公式，教師引導學生從三角形的判斷進行逆向推理，并鼓勵他們做一回“數學家”，動手得出自己的理論.

隨后，學生通過計算教材出現的各種形狀的三角形后發現：直角三角形的最大邊的平方正好等于另外兩邊平方之和，這剛好論證了“勾股定理”的說法. 更有趣的是，大量實際測量數據證明：銳角三角形最大邊的平方小于另兩邊平方之和，而鈍角三角形最大邊的平方大于另兩邊平方之和. 學生通過動手實踐、測量，不僅論證了勾股定理，并且探索出用勾股定理的逆定理進行三角形形狀的識別與判斷的方法，這對于學生探索精神與創造能力的激發非常有幫助.

隨著時代對人才要求的不斷變化，葆有工匠精神、擁有扎實專業、富有創新精神的人才能在激烈的社會競爭中“激流勇進”. 學生自身能力的提升與學校教育息息相關，作為教師本身不僅要專注于傳授學科知識，更要在豐富而先進的教學理念中不斷激發學生的多元潛能. 初中數學課堂是學生潛能激發的優質平臺，教師要讓學生從實際出發，運用所學知識，發現數學現象、提出并解決數學疑問，進而發展數學，提升自我.