利用勾股定理列方程在線段長度問題中的應用
深圳市南山實驗教育集團南海中學(518054) 孫夏林
利用勾股定理列方程在線段長度問題中的應用
深圳市南山實驗教育集團南海中學(518054) 孫夏林
在本人這幾年的教學中,發現剛升上初二的學生對求線段長度的問題比較吃力,在這個階段方法不多,所以有時無從下手.在這里,我就利用勾股定理列方程解決此類問題,做一個分析和歸納.
1.斷樹問題:
例1.如圖,一棵大樹被臺風吹斷,頂端落在離大樹底部8米處,已知大樹原長16米,求大樹斷開處的高度.
分析:此題問高度,設斷開處的高度為X米,倒下部分為(16?x)米,根據勾股定理列方程X2+82=(16?X)2即可求出答案.此題是勾股定理的基本題型,方法是直接列方程求解.與之類似的還有旗桿問題,蘆葦問題等等.
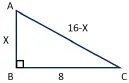
圖1
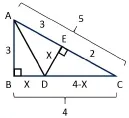
圖2
2.折疊問題:
例2.在直角三角形ABC中,∠B=90°,沿AD折疊后,使B落在斜邊AC上,若AB=3,BC=4.求BD的長度.
分析:此題為折疊問題,折疊后構造出直角三角形,計算問題常需要借助方程思想方法解證.此外,本題求垂線段DE長度,三角形各邊已知.還可利用等面積法列方程求高.

3.公共邊問題:
例3.在直角三角形ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15,求AD長.
分析:本題為常見的求直角三角形中線段問題,方法很多.但對于剛接觸勾股定理的初一學生來說,他們較常用的是等面積法求斜邊上的高CD,再在直角三角形ACD中利用勾股定理求AD.在學生充分思考后,我提出能否不先求CD而直接求AD,并引導他們思考圖中各條線段的數量關系,最后有學生就發現,兩個小直角三角形有公共的直角邊CD,把這個作為橋梁,就可列出含有AD的方程求解了.
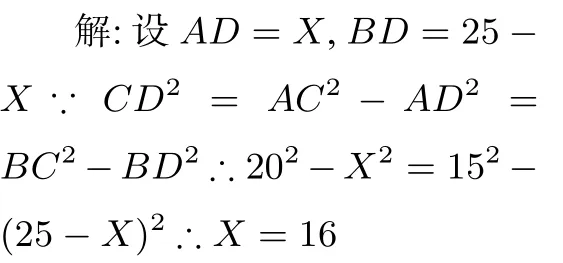
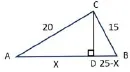
圖3
變式1.已知三角形ABC,AB=63,BC=30,AC=51.求三角形面積.
分析:本題已知三角形三邊求面積,就是先求高.由于不是直角三角形,等面積法不適用.然后學生發現這一題的圖和例3很像,也是兩個直角三角形有一條公共直角邊,于是他們用剛才的方法嘗試了一下,問題迎刃而解.

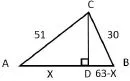
圖4
變式2.在三角形ABC中,∠C=90°,點M在BC上,若AB=17,AM=10,BM=9,求AC,CM的長.
分析:本題和前兩例類似,只不過兩個直角三角形在公共直角邊的同一側了,方法還是利用公共直角邊列方程.學生在做完前兩個題時,大多數基本上能想到這種思路.
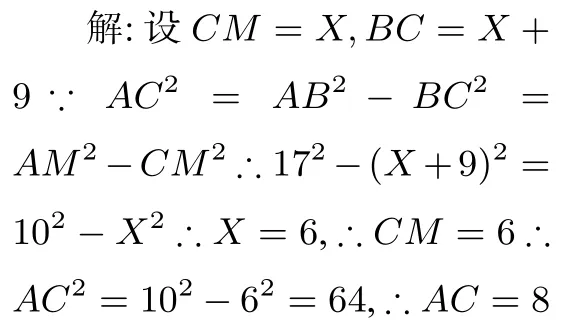
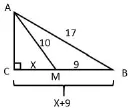
圖5
變式3.在三角形ABC中,AB=AC=20,BC=32,BM=9,D是BC上一點,且.AD⊥AC,求BD的長.
分析:此題中,不再是兩個三角形有公共直角邊,而是其中一個三角形的直角邊是另一個三角形的斜邊,學生在觀察思考后,發現只要是公共邊就能列出方程,從而達到了思維的靈活性.

