無痕教育的課堂實踐策略
——以《解決問題的策略》教學為例

徐　斌（特級教師）

理想的教育境界是教育無痕，然而“有”和“無”并不是完全對立矛盾，而是具有內在聯系的統一體。如何處理有痕與無痕之間的辯證統一關系呢？有痕，體現的是基礎知識和基本能力的顯性變化；無痕，體現的是必備品格和關鍵能力的隱性提升。有痕，更多地表現為課堂組織設計的精致與細膩；無痕，更多地表現為課堂教學過程的靈動與開放。有痕與無痕，是互相依存的和諧統一。要達到無痕的境界，需要經歷有痕的階段。在我看來，教育的最終目的是要讓學生獲得帶得走、看不見而又用得著的東西，即當下都在研究與提倡的核心素養。核心素養是學生發展的“隱形的翅膀”，具有“無形的力量”，如同武俠小說里面的“手中無劍，劍在心中”。無痕教育理念下的數學課堂實踐策略有哪些呢？下面以六年級《解決問題的策略：替換》一課的教學為例，闡述其教學實施策略。

一、不知不覺中開始

良好的開端是成功的一半，數學學習活動的開啟，應該在自然而然中出發，而不是赤裸裸地灌輸和強制性接受。只有引發了對新知的內在需要，才能激發起學生學習的內驅力。而要做到“不知不覺中開始”，前提是教師對所教內容的整體把握。優秀的教師總是能夠瞻前顧后、遷移滲透，把握所教內容與以前學習內容以及將來學習內容之間的實質性聯系，幫助學生選準合適的認知起點，讓學生在不知不覺中開始新知學習。

片斷1：引入“替換”的策略

（依次出示兩幅天平圖，引導學生觀察思考）

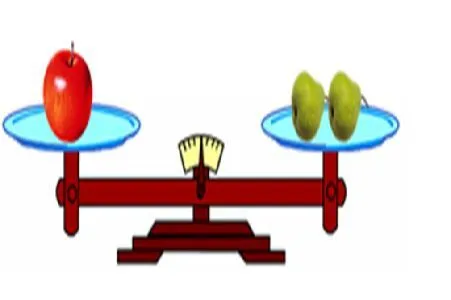
圖1

師：這是一架平衡的天平，從圖中你能看出一個蘋果的重量和一個梨的重量之間有什么關系嗎？（圖1）

生：一個蘋果的重量是一個梨的兩倍。

師：據兩幅天平圖，你能求出一個蘋果和一個梨的重量嗎？

生：把圖2中左邊的一個蘋果換成兩個梨，就成了4個梨重400克，這樣可以求出一個梨重100克，再求出一個蘋果重200克。

生：把圖2中左邊兩個梨換成一個蘋果，就是兩個蘋果重400克，一個蘋果就重200克，再求出一個梨重100克。

（課件動態演示把一個蘋果換成兩個梨或者把兩個梨換成一個蘋果）

師：在解決剛才這個問題時，大家用到了“換”的方法，這是數學中一種非常重要的策略——替換。（板書）

師：其實早在一千七百多年前有一個叫曹沖的小朋友，就用替換的策略演繹了一個生動的故事，你們聽說過嗎？

師：（出示“曹沖稱象”的圖片）曹沖是如何用替換的辦法稱出了大象的重量？

生：曹沖是用石頭替換大象的。

【解讀：如何讓學生在不知不覺中產生運用替換策略的需要？上述教學片斷中，通過形象直觀的方式引發了學生的初始學習進程。學生雖然是第一次正式學習用替換的策略解決問題，但在他們的生活經驗中已模糊地經歷過類似的方法，只是還沒有建立起一種完整的數學模型。所以在課的引入部分，從直觀的天平圖，到感性的數形結合，再到抽象的推理計算，并結合“曹沖稱象”的典故，一下就扣住學生心理，喚醒了他們頭腦里的已有生活經驗，為之后的探究過程奠定了良好的心理準備和認知基礎。】

二、潛移默化中理解

“為理解而教”是數學教學的重要目標，而理解知識的關鍵是順應學生的思維特點和認知規律。小學階段學生的認知水平屬于“具體運算思維”階段，其最大的特點是思維離不開具體事物的支持，他們的感知覺、觀察力和記憶均處于初步發展水平，學習數學的動機和興趣也很不穩定。在這樣的前提之下，小學生學習數學的過程，需要充分借助形象直觀的教學手段，充分利用新舊知識的相互作用，以順應學生的學習心理，讓他們在不露痕跡中獲得新知意義。

片斷2：理解“替換”的本質

例題：小明把720毫升果汁倒入6個小杯和1個大杯，正好都倒滿。小杯的容量是大杯的小杯和大杯的容量各是多少毫升？

生：大杯容量是小杯的3倍。

生：1個大杯可替換成3個小杯。

生：3個小杯可替換成1個大杯。

師：怎樣用替換的策略來解決這個問題呢？誰能把你的方法介紹給大家？

生：我把1個大杯換成3個小杯，這樣就有9個小杯，一共是 720 毫升，720÷9＝80，可以算出一個小杯的容量是80毫升，一個大杯的容量就是240毫升。

生：我是把6個小杯換成2個大杯，這樣就有3個大杯，720÷3＝240，先求出一個大杯的容量是240毫升80，再求出一個小杯的容量是80毫升。

師：如果把題中條件改成“大杯的容量比小杯多20毫升”，現在還可以替換嗎？

生：我認為不好替換。因為不是正好裝720毫升果汁。

生：我認為似乎可以替換，就是替換之后有可能720毫升果汁裝不下。

生：我也認為可以替換，不過替換之后也有可能不止裝720毫升果汁。

師：請同學們在練習紙上畫圖試一試，看看能否解決問題。不過要特別注意——在替換時，果汁的總量會有什么樣的變化？

（教師完成板書）

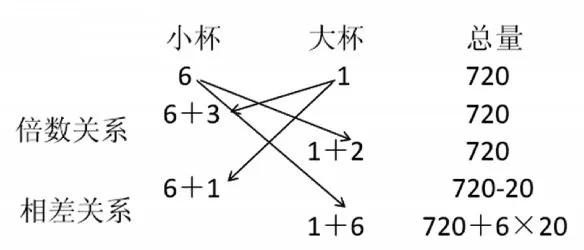
【解讀：如何讓學生在潛移默化中理解替換策略的本質？上述片斷中，先讓學生自主分析數量關系，然后組織小組討論尋求策略，接著獨立畫圖感悟思考，最后師生交流，教師用簡潔明了的板書加以體現。尤其是板書的設計具有啟發性，采用箭頭符號，讓學生直觀地感知大、小杯替換的過程。在學生初步學習了倍數關系的替換策略之后，教師抓住替換的依據進行變式，由“小杯的容量是大杯的”改變為“大杯的容量比小杯多20毫升”。當學生對兩個數量呈相差關系能否進行替換產生不同意見時，適時組織學生討論、辯論，從而獲得問題的解決。這樣的設計與教學，抓住兩個量之間的關系，靈活變化，充分調動了學生的探究欲望，利用知識間的遷移，突破了難點，并讓學生在比較中內化已有知識結構，明確了倍比、差比兩種不同類型的替換特征，在變化與不變中讓學生探尋聯系，感受到數學的規律美。】

三、循序漸進中掌握

學生學習數學的過程，既是在教師引導下的意義建構過程，也是在自身需求發展中的自主建構過程。數學教學是一種層次藝術，更是一種“進”與“退”的智慧。通過適當的“退”和必要的“進”，能使得學習過程成為學生潛移默化地掌握知識和技能的過程。表面上看，“進”和“退”是一對反義詞，然而，這兩者并不矛盾。從某種意義上說，“退”是“進”的準備和基礎，“進”是“退”的發展與提升。在課堂上，“進”“退”之間體現的是一種行云流水般的從容節奏，是一種水乳交融般的無痕狀態。

片斷3：掌握“替換”的策略

1.學生獨立審題，填寫替換的方法，不必列式計算：

（1）六（1）班 50名同學和楊老師、杜老師一起去參觀機器人科普展，買門票一共用去270元。已知每張成人票是每張學生票的兩倍，每張學生票多少元？每張成人票多少元?

想：把它們都看成（ ）票，可以把（）張（）票換成（）張（）票。那么270元相當于買了（）張（）票。

（2）在兩個同樣的大盒和五個同樣的小盒里裝滿球，正好是100個。每個大盒比每個小盒多裝8個，每個大盒和每個小盒各裝多少個？

想：如果把（ ）個（ ）盒換成（）個（ ）盒，總個數比原來（ ）（填“多”或“少”）（）個。

2.你能運用替換的策略解決這個問題嗎？

（部分學生看到題目就開始列式，部分學生沒有馬上列式，少數學生舉手發問）

生：這道題似乎缺少什么條件？

生：這道題目沒有告訴我們鉛筆和鋼筆單價之間的關系，因此不能做。

師：不錯，聰明的同學善于發現問題！如果運用替換的策略，就需要明白替換的依據。那么，要想用替換的策略解決這個問題，可以補充什么樣的條件？

生：可以補充倍數關系的條件，也可以補充相差關系的條件。

【解讀：有效的數學課堂不能止步于理解。為促進學生從理解走向掌握，上述片斷中設計了兩個層次的鞏固練習：前兩題是獨立審題并填寫替換方法，進行基礎性練習，其實是一種“退”；最后一題是缺少條件的替換問題，讓學生嘗試與討論，并補充相關條件，其實是一種“進”。這樣的設計與教學，學生在循序漸進中逐步走向替換策略的本質，形成相關技能，進而應用技能解決簡單的實際問題。】

四、春風化雨中提升

課堂學習的過程就是學生不斷發展和提升的過程。如何提升學生的數學素養？有道是：比知識更重要的是方法，比方法更重要的是思想，比思想更重要的是精神。課堂是師生人生中一段重要的生命經歷，課堂是充滿無限魅力的地方，課堂是學生充分發展的天空。無痕教育理念下的數學課堂，學生的學習經歷應是充實快樂的，學習結果應是充分有效的，學習的過程應是充滿智慧的。

片斷4：拓展“替換”的策略

師：剛上課時，我們觀察了天平圖，采用了替換的策略分別求出了兩種水果的重量。現在我們繼續觀察天平圖。

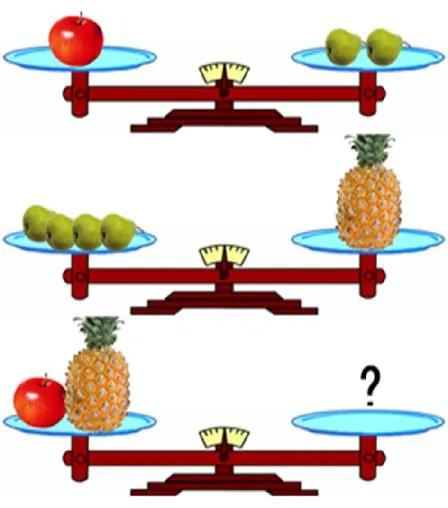
師：第一幅天平圖，顯示了兩種水果之間的重量關系；第二幅天平圖，出現了第三種水果——菠蘿；第三幅天平圖，右邊托盤里，如果放同一種水果，可以怎樣放？

生：可以放6個梨。

生：可以放3個蘋果。

生：可以放一個半菠蘿。

師：如果右邊托盤里放了一個600克的砝碼，天平保持平衡。你能分別求出一個梨、一個蘋果和一個菠蘿的重量嗎？

【解讀：學生學習數學的重要價值在于發現生活中的數學問題，并能利用所學的知識去解決問題。數學又是思維的體操，思維的靈活性、開放性、應變性直接關系到學生學習能力的高低。本課主要學習的是兩個量之間的替換，而此題已經拓展為三個量之間的替換，學生的思維能力得到極大的提高與開發。在課的結尾再次結合課始的直觀天平圖，并進行拓展和延伸，讓學生感受到替換策略的作用，去尋找生活中的替換現象，并從數學的角度去研究這些現象，進而從數學策略上升為數學思想，乃至于數學的理性精神。】