學(xué)會“挖井”思維

任衛(wèi)兵（特級教師）

【教學(xué)內(nèi)容】

蘇教版六年級上冊第21頁。

【教學(xué)過程】

一、出示習(xí)題

（出示數(shù)學(xué)書第21頁的一道習(xí)題）

用1立方厘米的正方體木塊堆成的兩個長方體，分別正好裝滿各自右邊的容器。你知道這兩個容器各能盛多少毫升水嗎？

師：要比較兩個容器的容積大小，如果不測量和計算，我們可以怎樣比？

師：為了便于表達(dá)，我們可以把左邊的容器叫做甲容器，右邊的為乙容器。誰來說說你的想法？

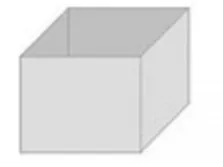
甲

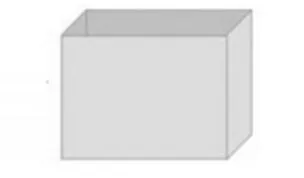
乙

師：把甲容器裝滿水，倒入乙容器，可能會出現(xiàn)幾種情況？

生：第一種情況，甲容器倒空，乙容器未滿，乙容器的容積大；第二種情況，甲容器倒空，乙容器正好裝滿，甲、乙容器的容積一樣大；第三種情況，甲容器未空，乙容器裝滿，甲容器的容積大。

師：無論是上面的哪一種情況，兩個容器中水的體積和總是怎樣的？

生：兩個容器中水的體積和是不變的。

【設(shè)計意圖：在學(xué)生學(xué)習(xí)了《長方體和正方體》單元知識后，需要對本單元進(jìn)行一次整理和復(fù)習(xí)。通過知識梳理和變式練習(xí)是一條路徑；借助書本習(xí)題，引導(dǎo)學(xué)生從不同的視角挖掘出新的問題，從而將相關(guān)知識有機(jī)統(tǒng)整到一起，則是另一條路徑。后一種路徑比起前一種來，可能更具挑戰(zhàn)性，更易激發(fā)學(xué)生的問題意識和探究欲望。】

二、拓展練習(xí)

拓展一：

師：現(xiàn)在我們從里面測量了甲容器的長是6厘米，寬5厘米，高（或深）4厘米，乙容器長7厘米，寬3厘米，高5厘米。

師：我們把甲容器裝滿水，再倒入乙容器。裝滿后，你們能提出哪些問題？

生：甲容器中剩下的水的體積是多少立方厘米？

生：甲容器中剩下的水的高度是多少厘米？

生：甲容器中剩余部分的空間有多大？

師：同樣把甲容器裝滿水，再倒入乙容器。但這一次不倒?jié)M，如果要使兩個容器中的水面一樣高，你們能求出現(xiàn)在兩個容器中的水深都是多少厘米嗎？

（全班交流，請小組代表介紹各自的解決方案）

第一種想法：因為兩個容器中水的體積和是不變的，還等于原來甲容器中的水的體積，所以我們可以列方程來解答。解：設(shè)現(xiàn)在兩個容器中的水深都是x厘米。5×6×x+7×3×x=5×6×4。最后求出這個方程的解是。

師：兩個容器中水的高度是一樣的，我們都用字母h來表示，底面積不同，分別用字母S1、S2來表示，那么兩個容器中水的體積和就可以用什么來表示？（S1h＋S2h）還有其他的表示方法嗎？

生：還可以應(yīng)用乘法分配律，用（S1＋S2）h 來表示。

師：那如果不列方程，還可以怎樣求現(xiàn)在兩個容器中的水深呢？

第二種想法：我們可以假設(shè)把兩個容器粘在一起，然后抽調(diào)中間的隔板，再把水重新倒入這個特別的容器中。用原來甲容器中水的體積，除以兩個容器的底面積的和，也可以求出現(xiàn)在的水深。列式為（5×6×4）÷（5×6＋7×3）。

師：剛才的兩種解法，如果細(xì)細(xì)觀察，還是能發(fā)現(xiàn)它們之間是有聯(lián)系的。有興趣的話，課后還可以從“比”這個角度去想想其他的一些解法。

【設(shè)計意圖：在比較兩個容器的容積大小時，如果不測量和計算，而用倒水的方法來比較，那么可能會有幾種不同的情況呢？引導(dǎo)學(xué)生全面地思考問題，需要自然、無痕地進(jìn)行滲透。在學(xué)生列舉出所有可能的情況后，教師適時地總結(jié)出無論哪一種情況，兩個容器中的水的體積和是不變的，這也為接下來解決“兩個容器中的水深相等”這一問題做了鋪墊。教會學(xué)生“挖井”思維，需要教師適當(dāng)?shù)貫閷W(xué)生鋪設(shè)一個臺階，確定一個大致方向，這樣才便于學(xué)生積累一定的經(jīng)驗。只有當(dāng)學(xué)生有了自己的經(jīng)驗后，別人的經(jīng)驗才能夠接得上去。】

拓展二：

師：剛才我們是從體積（容積）這個角度來提出、解決新問題的，下面我們換個視角，來看這兩個長方體，你們又能提出哪些新問題呢？

課件出示：

師：如果把這兩個長方體表面涂漆，再切成1立方厘米的小正方體，那么三面、兩面、一面涂色以及六個面都未涂色的小正方體各有多少個呢？你們覺得這個問題與“表面涂色的正方體”有哪些相同之處？又有哪些不同呢？

師：同桌兩人分工，一起來算一算：把第一個長方體切開后，各種涂色小正方體的個數(shù)。

【設(shè)計意圖：從“表面涂色的正方體”拓展到“表面涂色的長方體”，不僅能讓學(xué)生更好的掌握長方體和正方體的特征，更有利于學(xué)生建構(gòu)相應(yīng)的模型，積淀數(shù)學(xué)思想。】

拓展三：

1.比較這兩個長方體，你還有什么不同的發(fā)現(xiàn)？

（適當(dāng)提示：剛才我們分別從體、面這幾個角度發(fā)掘出了新問題，如果從棱的角度呢？）

2.大家注意到?jīng)]有，這兩個長方體的棱長總和怎樣？（都是60厘米）根據(jù)這一特點，你又能提出什么新問題呢？

（棱長總和是60厘米的長方體，體積最大是多少？最小是多少？）

師：還可進(jìn)一步提煉為棱長總和相等的長方體或正方體，誰的體積最大？

3.尋求策略。

師：棱長總和是60厘米的長方體，有多少種不同的情況？解決這類問題適合采用哪種策略？

（那我們可以從哪一種情況開始列舉呢？）

4.合理猜想。

師：通過不完全列舉，你能提出什么猜想？

（棱長總和相等的長方體和正方體，正方體的體積最大。）

【設(shè)計意圖：也許教材編寫者也沒有意識到書本習(xí)題中的兩個長方體的棱長總和恰好相等，教師敏銳地捕捉到了這一特點，引導(dǎo)學(xué)生提出問題“棱長總和相等的長方體和正方體，誰的體積大”，并通過有序列舉、不完全列舉，啟發(fā)學(xué)生大膽地提出自己的猜想。可見，“大問題教學(xué)”并非一定要確定一個多大、多綜合的問題，有時一個小問題一樣能作出大文章。】

拓展四：

如果這是一個封閉容器，不小心在它的前面破了個洞，洞口下端距底面2厘米。這個容器最多能裝水多少毫升呢？

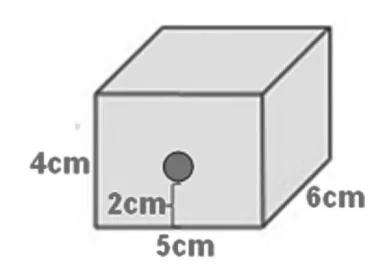
師：有認(rèn)為能裝水60毫升的同學(xué)嗎？還有不同的答案嗎？說說你是怎么想的？

【設(shè)計意圖：學(xué)會“挖井”思維，并非一味地求綜合、求深入，有時還要學(xué)會應(yīng)變。一個有破洞的容器最多能裝多少水，如果固守著底面不變，那么只能得到60毫升的結(jié)果，可是如果能靈機(jī)一動，把容器翻轉(zhuǎn)一下以后面作底面，讓洞口朝上，那么最多就能裝水120毫升。不僅能入乎其內(nèi)，還要能出乎其外，學(xué)會知入知出，才能彰顯出智慧。】

三、總結(jié)

師：通過這堂課的學(xué)習(xí)，你們對“學(xué)會‘挖井’思維”又有了哪些新的體會？（同一個問題，換個角度去看，就會有不同的發(fā)現(xiàn)）正所謂：思維一變天地寬，知入知出顯智慧。