數形結合在圓錐曲線中的應用

☉江蘇省蘇州第十中學校 陳 蕾

數形結合在圓錐曲線中的應用

☉江蘇省蘇州第十中學校 陳 蕾

高考數學“考綱”明確地指出，高考不僅要對學生的基礎知識、基礎能力進行考核，還要加強學生的數學思想、數學思維的考查，而數形結合就是現階段高中最重要的數學思想之一，幾乎在每一套高考數學試卷中，都會出現對數形結合思想的考查.數形結合的考查方式也有很多，比如圓錐曲線、函數、三角函數、數列，還有線性規劃，這些都可以考查學生對數形結合思想的掌握情況.在數學學習和解題過程中，要善于運用數形結合的方法來尋求解題途徑，制定解題方案，養成數形結合的習慣，解題先想圖，以圖助解題.用好數形結合的方法，能起到事半功倍的效果，用一句話來形容就是，“數形結合千般好，數形分離萬事休”.下面本文將介紹一下數形結合思想在圓錐曲線中幾類常見題型中的應用.

一、直線和圓錐曲線的位置關系

計算Δ=64k2-4（m+4k2）（4-4m）.

令Δ≥0，可解得m≥1且m≠4.

解法2（數形結合解法）：根據直線l：y=kx+1的方程

評注：（1）解法1是學生通常能想到的解法，雖然想法很簡單，但是解題的計算量很大，對于計算能力不強的同學來說，難度還是很大的.解法2的中心思想是利用圖形本身的性質，如果直線和橢圓至少有一個交點的話，也就是說直線和橢圓一定是相切或者相交的，換句話說就是直線所過的定點一定要在橢圓上或者橢圓內.（2）如果直線中只含有一種參數，則直線一定經過定點，把含有參數的項合并在一起，然后令等式兩端為零，即可得出所過定點坐標.

二、距離問題

例2如圖1所示，M是拋物線y2=4x上的一個點，F是拋物線的焦點，∠MFx=60°，求|FM|.

解法1（普通解法）：因為∠MFx=60°，所以直線MF的斜率

圖1

與拋物線方程聯立可得一元二次方程3x2-10x+3=0，解得

所以可以最終確定M的坐標為（3，2■3）.

又|NH|=|GF|=2，

所以m=4，即|MF|=4.

圖2

評注：（1）解法1是常規辦法，根據直線的傾斜角得出直線的斜率，進而設出直線方程，通過聯立解出M點的坐標，最后利用兩點之間的距離公式來解出最后答案.此方法想法簡單，一般同學都可以想到，但缺點是計算量較大，對于計算能力差的同學來說，不僅浪費時間，還不容易得出正確答案.（2）解法2利用數形結合，作垂線之后，形成一個特殊的直角三角形，利用圖形本身的數量關系來解出所需要的|MF|值，此種解法雖然需要作輔助線，但是計算量極大簡化，即使計算能力不好，也很容易得出正確答案，推薦同學們使用此種解法，在今后的學習中，要注意總結.

三、參數取值范圍問題

例3已知直線l過點D（0，3），且與橢圓4x2+9y2=36交于不同兩點M、N，設實數λ的取值范圍.

解法1（普通解法）：如圖3，設M（x1，y1），N（x2，y）2.

圖3

當直線l的斜率不存在時，由于，且λ＜0，

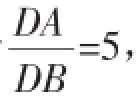
易知λ=-5或

當直線l的斜率存在時，設l：y=kx+3，聯立方程

消去y，得（9k2+4）x2+54kx+45=0.①

由①得Δ=（54k）2-180（9k2+4）＞0，

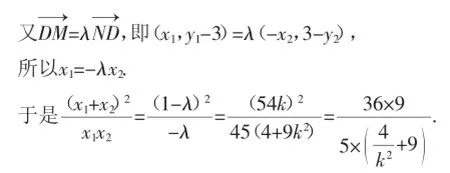
圖4

因為直線l繞點D在直線l1和y軸之間旋轉時，

數形結合的方法在高中數學的應用非常廣泛，本文只是給出了在圓錐曲線題目中的幾個應用，篇幅有限，還請廣大數學同仁給予批評和指正.