從數(shù)學(xué)核心素養(yǎng)看高等數(shù)學(xué)教學(xué)

羅 靜

（韶關(guān)學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院， 廣東 韶關(guān) 512005）

從數(shù)學(xué)核心素養(yǎng)看高等數(shù)學(xué)教學(xué)

羅 靜

（韶關(guān)學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院， 廣東 韶關(guān) 512005）

數(shù)學(xué)思想是大學(xué)數(shù)學(xué)核心素養(yǎng)最重要的內(nèi)容，當(dāng)前大學(xué)數(shù)學(xué)課程存在重計(jì)算輕思想的現(xiàn)象，偏離了培養(yǎng)“數(shù)學(xué)核心素養(yǎng)”的目標(biāo)，然而良好的數(shù)學(xué)素養(yǎng)對(duì)學(xué)生未來(lái)成就將發(fā)揮重要的作用。以《高等數(shù)學(xué)》課程為例，討論如何在教學(xué)中滲透數(shù)學(xué)思想，幫助學(xué)生學(xué)會(huì)數(shù)學(xué)思維，進(jìn)而逐步形成人生發(fā)展所必須的“核心素養(yǎng)”。

數(shù)學(xué)核心素養(yǎng)；數(shù)學(xué)思想；高等數(shù)學(xué)教學(xué)

“核心素養(yǎng)”是當(dāng)下教育領(lǐng)域的一個(gè)新熱點(diǎn)，是2014年3月教育部印發(fā)的《關(guān)于全面深化課程改革、落實(shí)立德樹(shù)人根本任務(wù)的意見(jiàn)》中提出來(lái)的，是課堂改革、教學(xué)方式改革的重要方向。在義務(wù)教育階段，數(shù)學(xué)教學(xué)中如何落實(shí)“核心素養(yǎng)”培養(yǎng)有一系列的理論研究與實(shí)驗(yàn)驗(yàn)證，并已取得卓越的成果。但關(guān)于大學(xué)階段最重要的數(shù)學(xué)公共課程《高等數(shù)學(xué)》該如何培養(yǎng)“核心素養(yǎng)”的研究寥寥無(wú)幾，本文將就高等數(shù)學(xué)教學(xué)該如何落實(shí)“核心素養(yǎng)”展開(kāi)初步的探討。

一、“數(shù)學(xué)核心素養(yǎng)”與“數(shù)學(xué)思想”

“數(shù)學(xué)核心素養(yǎng)可以理解為學(xué)生學(xué)習(xí)數(shù)學(xué)應(yīng)當(dāng)達(dá)到的有特定意義的綜合能力”，“核心素養(yǎng)基于數(shù)學(xué)知識(shí)技能，又高于具體的數(shù)學(xué)知識(shí)技能，核心素養(yǎng)反映數(shù)學(xué)本質(zhì)與數(shù)學(xué)思想，是在數(shù)學(xué)學(xué)習(xí)過(guò)程中形成的，具有綜合性、階段性和持久性。”［1］

“學(xué)科核心素養(yǎng)，粗略的說(shuō)是指凸顯學(xué)科本質(zhì)，具有獨(dú)特、重要育人價(jià)值的素養(yǎng)。”［2］

以上兩種說(shuō)法，是專家基于多年對(duì)義務(wù)教育階段數(shù)學(xué)教育研究和實(shí)踐得出的關(guān)于“核心素養(yǎng)”理解。《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》明確提出10個(gè)核心素養(yǎng)，即數(shù)感、符號(hào)意識(shí)、空間觀念、幾何直觀、數(shù)據(jù)分析觀念、運(yùn)算能力、推理能力、模型思想、應(yīng)用意識(shí)和創(chuàng)新意識(shí)。在完成了義務(wù)教育和高中階段學(xué)習(xí)后，學(xué)生已基本具備以上“核心素養(yǎng)”，那么在大學(xué)階段數(shù)學(xué)教育中，我們?cè)撊绻M(jìn)一步培養(yǎng)學(xué)生“核心素養(yǎng)”呢？

在高等數(shù)學(xué)教學(xué)中，我們關(guān)注的不是獨(dú)立的知識(shí)點(diǎn)是否掌握，而是數(shù)學(xué)思想方法或者數(shù)學(xué)整體知識(shí)的領(lǐng)悟和控制，希望學(xué)生通過(guò)高等數(shù)學(xué)學(xué)習(xí)，建立起認(rèn)識(shí)、分析和解決社會(huì)事務(wù)所具備的思維品質(zhì)。“數(shù)學(xué)邏輯結(jié)構(gòu)的一個(gè)特殊的最重要的要素是數(shù)學(xué)思想，整個(gè)數(shù)學(xué)科學(xué)就是建立在這些思想的基礎(chǔ)上，并按照這些思想發(fā)展起來(lái)的。”［3］所謂數(shù)學(xué)思想“一是數(shù)學(xué)產(chǎn)生以及數(shù)學(xué)發(fā)展過(guò)程中所必須依賴的那些思想。二是學(xué)習(xí)過(guò)數(shù)學(xué)的人所具備的思維特征。”［4］所以，在完成了基礎(chǔ)教育數(shù)學(xué)課程后，高等數(shù)學(xué)核心素養(yǎng)應(yīng)落足于一個(gè)能統(tǒng)領(lǐng)全局、獨(dú)特且不可替代的數(shù)學(xué)靈魂——數(shù)學(xué)思想。

綜上所述，數(shù)學(xué)思想是高等數(shù)學(xué)核心素養(yǎng)最重要的內(nèi)容，其最突出的特點(diǎn)是具有綜合性和持續(xù)性，并具有其他學(xué)科不可取代的育人價(jià)值。

二、“數(shù)學(xué)核心素養(yǎng)”與《高等數(shù)學(xué)》教學(xué)

“三種基本思想，即抽象、推理和模型”［4］。這三種思想，涵蓋了數(shù)學(xué)的起源、數(shù)學(xué)科學(xué)的形成和發(fā)展、數(shù)學(xué)與現(xiàn)實(shí)世界的聯(lián)系，最具有本質(zhì)意義的重要思想，其培養(yǎng)的邏輯思維能力及廣泛的應(yīng)用性，正是高等數(shù)學(xué)課程最核心的教學(xué)目標(biāo)。

“數(shù)學(xué)雖不研究事物的質(zhì)，但任一事物必有量與形，所以數(shù)學(xué)是無(wú)處不在，無(wú)時(shí)不用的。”［5］例如，定積分概念與性質(zhì)教學(xué)中最經(jīng)典的引例——曲邊梯形的面積，通過(guò)劃分、近似、求和與逼近四個(gè)步驟，計(jì)算不規(guī)則圖形的面積，及變速直線運(yùn)動(dòng)的路程計(jì)算中，可以用同樣的思路解決問(wèn)題。從以上兩個(gè)例子可以看出，雖然要計(jì)算的量的實(shí)際意義各不相同，但這些量的計(jì)算方法和步驟都是相同的，反映在數(shù)量上可歸結(jié)為相同結(jié)構(gòu)的和式的極限，拋開(kāi)這些問(wèn)題的具體意義，可以抽象出定積分的概念。撥開(kāi)云霧看清事物的能力正是大學(xué)數(shù)學(xué)課堂該教給學(xué)生的“核心素養(yǎng)”。

歸納演繹推理也是高等數(shù)學(xué)常用的思維方式。在一些運(yùn)算的算理中，其實(shí)也用到了演繹推理的方法，如在學(xué)習(xí)不定積分的計(jì)算時(shí)，“看積分，想微分”是用微分、積分互為逆運(yùn)算的方法。而這個(gè)過(guò)程表述為，“因?yàn)?x是x2的一個(gè)原函數(shù)，所以∫2xddx=x2+c”，如果加上“積分與微分互為逆運(yùn)算”這個(gè)大前提，這就是一個(gè)完整的三段論推理。

模型思想的建立是學(xué)生體會(huì)和理解數(shù)學(xué)與外部世界聯(lián)系的基本途徑。建立和求解模型的過(guò)程包括：從現(xiàn)實(shí)生活或具體情境中抽象出數(shù)學(xué)問(wèn)題中的數(shù)量關(guān)系和變化規(guī)律，求出結(jié)果并討論結(jié)果的意義。在《高等數(shù)學(xué)（經(jīng)管類）》課程中，數(shù)學(xué)建模思想體現(xiàn)得淋漓盡致。

例1：（考研數(shù)學(xué)三2015年第17題）為了實(shí)現(xiàn)利潤(rùn)最大化，廠商需要對(duì)某商品確定其定價(jià)模型，設(shè)Q為該商品的需求量，P為價(jià)格，MC為邊際成本，η為需求的彈性（η＞0）。

（Ⅱ）若該商品的成本函數(shù)為C(Q)=1 600+Q2，需求函數(shù)為Q=40-P，試由（Ⅰ）中定價(jià)模型確定此商品的價(jià)格。

首先理清每個(gè)經(jīng)濟(jì)術(shù)語(yǔ)的定義，結(jié)合追求利潤(rùn)最大的現(xiàn)實(shí)，抽象出數(shù)學(xué)表達(dá)式，是解決這個(gè)問(wèn)題的關(guān)鍵。

解：（Ⅰ）利潤(rùn)函數(shù)L(Q)=R(Q)-C(Q)=QP-C(Q)，其中R(Q)為總收益函數(shù)，C(Q)為總成本函數(shù)。

從上述例子可以看出，抽象、推理和模型思想在大學(xué)專業(yè)課程學(xué)習(xí)中同樣有這重要的作用。提倡“數(shù)學(xué)核心素養(yǎng)”就意味著對(duì)高等數(shù)學(xué)教學(xué)提出更高的要求，不是計(jì)算技巧和技能的培養(yǎng)，而是通過(guò)數(shù)學(xué)學(xué)習(xí)掌握數(shù)學(xué)思想，體會(huì)數(shù)學(xué)思維的作用進(jìn)而提高數(shù)學(xué)修養(yǎng)。

三、《高等數(shù)學(xué)》 “數(shù)學(xué)核心素養(yǎng)”的育人價(jià)值

在大學(xué)階段，學(xué)生除了學(xué)習(xí)某些必需的基礎(chǔ)知識(shí)、基本技能之外，更重要的是掌握如何獲得更多知識(shí)以及如何應(yīng)用知識(shí)解決各類問(wèn)題的能力。在茫茫的知識(shí)海洋中選取最恰當(dāng)?shù)姆椒ǎ纬煽尚械淖罴阉悸罚⒁画h(huán)一環(huán)有條不紊地解決問(wèn)題，這就是高等數(shù)學(xué)最不可取代的育人價(jià)值。所以，在高等數(shù)學(xué)的教學(xué)中，我們不應(yīng)只注重知識(shí)量的增加，應(yīng)該關(guān)注知識(shí)網(wǎng)絡(luò)的建構(gòu)，為捕抓人生的大魚(yú)作充足的準(zhǔn)備。本題主要運(yùn)用變上限求導(dǎo)公式和型函數(shù)的洛

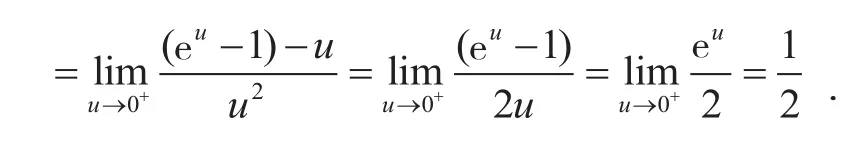
必達(dá)法則求極限。從復(fù)雜的式子中提取出本質(zhì)屬性，排除各種非本質(zhì)的屬性干擾，最終找到解決問(wèn)題的方法，通過(guò)高等數(shù)學(xué)的學(xué)習(xí)，培養(yǎng)學(xué)生的學(xué)習(xí)能力，面對(duì)各種復(fù)雜的情境，能獨(dú)立完成舍次求主的分析活動(dòng)。有一套相互關(guān)聯(lián)、環(huán)環(huán)相扣的知識(shí)網(wǎng)絡(luò)，積極主動(dòng)解決問(wèn)題的愿望和恰如其分提出關(guān)鍵問(wèn)題的能力，這是數(shù)學(xué)解題的必備條件，也將會(huì)在未來(lái)工作生活中發(fā)揮重要作用。

四、總結(jié)和展望

H.費(fèi)賴登塔爾有一句名言：“沒(méi)有一種數(shù)學(xué)思想，以它被發(fā)現(xiàn)時(shí)的那個(gè)樣子發(fā)表出來(lái)，一個(gè)問(wèn)題被解決以后，相應(yīng)的發(fā)展成一種形式化的技巧，結(jié)果使得火熱的思考變成了冰冷的美麗。”［6］這句話真實(shí)的反映了《高等數(shù)學(xué)》教學(xué)的現(xiàn)狀：教學(xué)就是講座，學(xué)習(xí)就是大量的練習(xí)。標(biāo)準(zhǔn)化的教學(xué)模式導(dǎo)致學(xué)生在模式化的教學(xué)中失去了學(xué)習(xí)數(shù)學(xué)的興趣，一成不變是課程標(biāo)準(zhǔn)扼殺了學(xué)科之間的交叉性，最終高數(shù)數(shù)學(xué)不可取代的育人價(jià)值就淹沒(méi)在冰冷的符號(hào)里。在今后的教學(xué)中，希望能借鑒中學(xué)課改的經(jīng)驗(yàn)，把活動(dòng)教學(xué)等能有效提高學(xué)生學(xué)習(xí)興趣的教學(xué)模式引入大學(xué)數(shù)學(xué)課堂，致力于培養(yǎng)學(xué)生淘金式思維，讓《高等數(shù)學(xué)》課程成為培養(yǎng)大學(xué)生核心素養(yǎng)最有利的工具。

［1］馬云鵬.關(guān)于數(shù)學(xué)核心素養(yǎng)的幾個(gè)問(wèn)題［J］.課程·教材·教法，2015（9）：36-39.

［2］曹培英.從學(xué)科核心素養(yǎng)與學(xué)科育人價(jià)值看數(shù)學(xué)基本思想［J］.課程·教材·教法，2015（9）：40-43.

［3］費(fèi)里德曼.中小學(xué)數(shù)學(xué)教學(xué)心理學(xué)原理［M］.陳心五.譯. 北京：北京師范大學(xué)出版社，1987：21.

［4］史寧中.漫談數(shù)學(xué)基本思想［J］.中國(guó)大學(xué)教學(xué)，2011（7）：9-11.

［5］中國(guó)科學(xué)數(shù)學(xué)物理部.今日數(shù)學(xué)及其應(yīng)用［J］.自然辯證法研究，1994（1）：5.

［6］張奠宙.微積分教學(xué)：從冰冷的美麗到火熱的思考［J］.高等數(shù)學(xué)研究，2006（2）：2-4.

A Review of High Mathematics from the Key Mathematical Competence

LUO Jing
（Department of Mathematics and Statistics，Shaoguan University，Shaoguan 512005，Guangdong，China）

Mathematics thought is the core of “key mathematical competences ”.There exists the phenomenon attaching importance to computations and neglecting ideas in college mathematics courses. Without a doubt, mathematics culture has important influence on the study and life. For example，in the course of calculus，it puts forward several suggestions of infiltrating mathematics thought ，makeing good use of the course to improve thinking and form the key mathematical competence.

key mathematical competence； mathematical thought； calculus teaching

G642.421

A

1007-5348（2017）05-0083-03

（責(zé)任編輯：邵曉軍）

2016-12-26

2015年韶關(guān)學(xué)院科研項(xiàng)目“韶關(guān)學(xué)院高等數(shù)學(xué)教學(xué)現(xiàn)狀調(diào)查研”（S201501021）

羅靜（1982-），女，廣東興寧人，韶關(guān)學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院講師，碩士；研究方向：數(shù)學(xué)教育、高等數(shù)學(xué)教育。