對三角函數(shù)“誘導(dǎo)公式”幾種導(dǎo)入方案的對比評說

馬娟平

[摘 要] 本文記錄在一次區(qū)級的評優(yōu)課中幾位參賽選手引入“誘導(dǎo)公式”的不同方案，然后筆者深入分析不同方案的優(yōu)劣以及適用性，提出針對不同的學生要有不同的“課堂引入”，讓“引入”能提高學生的學習興趣，提高學生對新知識的接受能力和理解能力，最終提高學生對數(shù)學的理解.

[關(guān)鍵詞] 誘導(dǎo)公式；課堂引入；教學方案；教學方案評說

在一次針對必修4中“1.2.3三角函數(shù)誘導(dǎo)公式”（第一課時）數(shù)學評優(yōu)課中，幾位選手的設(shè)計，在自然、思維及有效性等方面各有千秋. 我們知道，良好的開端是成功的一半，那么如何設(shè)計課堂導(dǎo)入更能貼近學生，更能激發(fā)學生的興趣，更趨合理？以下選取幾節(jié)有代表性的課堂導(dǎo)入，談?wù)劰P者的一些想法，與同行交流.

[?] 教材簡析

三角函數(shù)的誘導(dǎo)公式是三角函數(shù)的基礎(chǔ)，誘導(dǎo)公式的認知基礎(chǔ)是終邊所對角的三角函數(shù)定義、單位圓坐標表示、三角函數(shù)線. 教學目標是借助單位圓推導(dǎo)出正弦、余弦的誘導(dǎo)公式，能正確運用誘導(dǎo)公式將任意角的三角函數(shù)轉(zhuǎn)化為銳角三角函數(shù)，并解決有關(guān)三角函數(shù)的求值、化簡及證明問題.方法是從特殊推廣到一般，涉及轉(zhuǎn)化思想、數(shù)形結(jié)合思想.

[?] 方案呈現(xiàn)

1. 方案1：復(fù)習引入

（1）在平面直角坐標系中，任意角α的正弦、余弦、正切是如何定義的？

學生由任意角的三角函數(shù)定義得：sinα=_____，cosα=_____，tanα=_____.

（2）為簡單起見，取r=1，選取角α的終邊與單位圓的交點為P（x，y）.

則sinα=_____，cosα=_____，tanα=_____. 此時P點的坐標可表示為_____.

探究新知：

請在單位圓中作出390°角的終邊，交圓周于點P，并根據(jù)任意角三角函數(shù)的定義求出：

sin390°=______________；

cos390°=______________；

tan390°=______________.

探究一：角的終邊與角α的終邊相同的三角函數(shù)值之間的關(guān)系. （略）

2. 方案2：問題串引入

的值嗎？

教師（解說）：大家可以看到，這兩個角的特征，一個大于360°，一個小于0°，這類角的三角函數(shù)值，該如何求？

讓學生探索1～2分鐘，說說想法.

通過畫圖，發(fā)現(xiàn)390°的終邊與30°的終邊相同.

教師：終邊相同的角的三角函數(shù)值有什么關(guān)系？

學生：相同.

教師：為什么？

過渡句：公式一可以將任意角的三角函數(shù)值，轉(zhuǎn)化為[0，2π]內(nèi)的角的三角函數(shù)值.那么對于[0，2π]內(nèi)非銳角的三角函數(shù)，能否轉(zhuǎn)化成銳角三角函數(shù)呢？

3. 方案3：教材引入

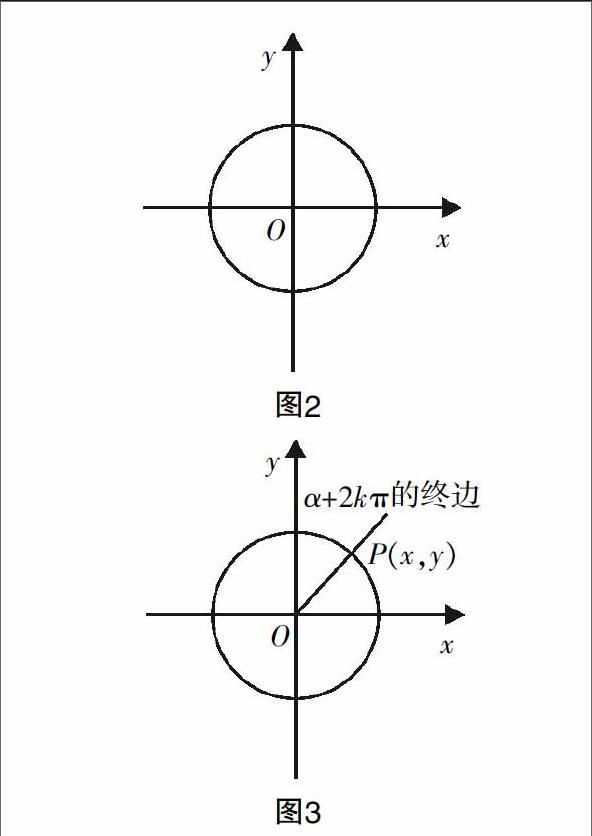
由三角函數(shù)的定義可以知道，終邊相同的角的同一三角函數(shù)值相等，即

sin（α+2kπ）=__________（k∈Ζ）；

cos（α+2kπ）=__________（k∈Ζ）；

tan（α+2kπ）=__________（k∈Ζ）.

除此之外還有一些角，它們的終邊具有某種特殊關(guān)系，如關(guān)于坐標軸對稱、關(guān)于原點對稱等，那么它們的三角函數(shù)值有何關(guān)系呢？如果角α的終邊與角β的終邊關(guān)于x軸對稱，那么α與β的三角函數(shù)值之間有什么關(guān)系？

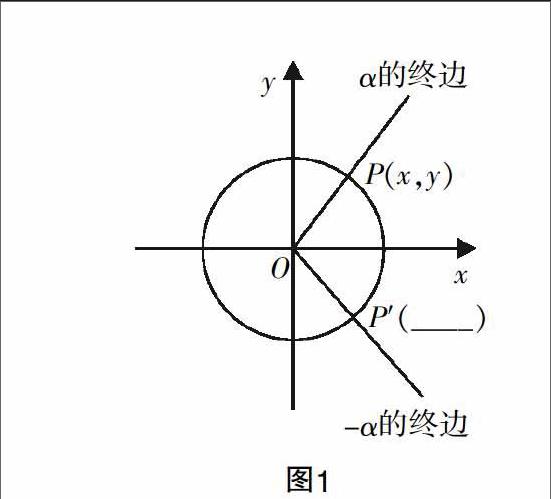
然后，設(shè)α與β與單位圓交于點P，P′，則P，P′關(guān)于x軸對稱，點P的坐標是（cosα，sinα），點P′的坐標是（cosβ，sinβ），則cosβ=cosα，sinβ=-sinα. 得到sin（-α）=-sinα，cos（-α）=cosα，tan（-α）=-tanα.

其他的類似可以求得.

4. 方案4：談話式導(dǎo)入

教師：前面，我們已經(jīng)學習了任意角，范圍擴大到大于360°或小于0°，學習了三角函數(shù)的定義、象限角及同角三角函數(shù)的關(guān)系式，研究三角函數(shù)的一個重要問題就是求值. 對于0～90°的角，借助數(shù)表或計算器都能求它們的三角函數(shù)值；對于90°～360°的角，大于360°的角，小于0°的角，該如何求它們的三角函數(shù)值呢？

我們先研究如何求大于360°的角和小于0°的角的三角函數(shù)值.

比如，sin390°=______. 請你嘗試解決一下.

學生畫出390°，部分學生聯(lián)想到單位圓，在單位圓上作出390°的角，其終邊交圓周于點P.

教師巡視，問：對你畫出的角有什么發(fā)現(xiàn)？

學生會發(fā)現(xiàn)390°的角的終邊與30°的角的終邊相同，教師要接著問“終邊相同的角的三角函數(shù)值有什么關(guān)系”.

生：根據(jù)任意角三角函數(shù)的定義，可得sin390°=sin30°.

教師：那么cos390°=_____，tan390°=_____.

學生輕松得出. （略）

教師：這個結(jié)論能推廣嗎？30°改成銳角α可以嗎？

學生不難得出：sin（360°+α）=sinα；cos（360°+α）=cosα，tan（360°+α）=tanα.

教師：當α為任意角時，公式還成立嗎？

……

[?] 對四種課堂導(dǎo)入方案的對比評說

新課程的基本理念是以學生的發(fā)展為本，一個好的教學方案，必須符合教學目標，符合學生的認知特點，因為數(shù)學學科的一個重要任務(wù)是培養(yǎng)學生的思維能力. 因此，課堂導(dǎo)入是否能產(chǎn)生思維的憤悱狀態(tài)，是否有利于學生進行思維訓練，是非常關(guān)鍵的. 而“強扭的瓜不甜”，學生對不自然的導(dǎo)入不容易接受，因此，要考慮課堂引入的自然性；又“興趣是最好的老師”，故課堂導(dǎo)入要考慮是否能激發(fā)學生的學習興趣；當然，課堂導(dǎo)入還要有益于學生理解數(shù)學，所以還應(yīng)考慮引入的有效性.由此，對以上四種方案進行簡要對比評說.

方案1是先復(fù)習舊知，從任意角的三角函數(shù)定義到單位圓上點的坐標，然后從單位圓中作出390°角的終邊進行探索.這樣從已知到未知，并融入數(shù)學文化：從布龍克爾（英）名句“圓是第一個最簡單、最完美的圖形優(yōu)化設(shè)計”，循序漸進，學生循著教師的步伐“走”，很容易走穩(wěn)，對知識容易理解，但都是教師事先安排好的，適宜于層次較低的學生.不足點：鋪墊偏多，留給學生思考的余地不大，長此以往，學生就會產(chǎn)生思維上的惰性，在面臨新問題時束手無策，缺乏經(jīng)驗，容易形成畏難心理. 方案1對學生的思維訓練顯得不足，有教師牽著學生走之嫌.

方案2是基于哈爾摩斯的名言“問題是數(shù)學的心臟”進行的問題驅(qū)動，先后提出了兩個富于挑戰(zhàn)性的計算問題. 問題1旨在研究對于大于360°的角或小于0°的角的三角函數(shù)求值，從解決問題的需要研究新知；問題2是為了引出需要求解在第四、第二、第三象限的角的三角函數(shù)值的問題而設(shè)置的，若設(shè)角α是第一象限角，則讓學生說出-α，π-α，π+α分別是第幾象限角. 問題1和問題2的共同點都是為了解決學習這五組誘導(dǎo)公式的必要性問題. 弄清了為什么要學習新知，明確了方向，就會產(chǎn)生自覺的行動. 問題3是誘導(dǎo)公式的基礎(chǔ)，也是學生理解的難點，即（cosα，sinα）. 若問題3解決了，則三個角-α，π-α，π+α的終邊都可以用三角函數(shù)值表示. 這三個問題解決好了，這五組誘導(dǎo)公式的意義建構(gòu)就完成了. 這種方案是從解決問題的角度出發(fā)的，促使學生產(chǎn)生憤悱的狀態(tài)，產(chǎn)生解決問題的愿望，凸顯其必要性. 這種方案有益于培養(yǎng)學生的思維能力，這種方案適宜于層次中等或中等以上的學生.

方案3是通過兩個角α，β特殊的對稱關(guān)系，求出單位圓上對應(yīng)的坐標關(guān)系，得出誘導(dǎo)公式. 提出的問題很自然，敘述簡約、清楚，也有利于學生理解數(shù)學，適宜層次中等及中等以下的學生.其不足點是沒有問題驅(qū)動來得強烈，不利于學生求知欲的激發(fā).

方案4是對教材方法的一種改造，通過與學生的對話引入. 其一，從已知逐漸過渡到未知，順應(yīng)學生的認知基礎(chǔ)，符合學生的認知規(guī)律，與學生做朋友，容易激發(fā)學生的興趣，形成了和諧的課堂氛圍；其二，引入、過渡很自然，亦步亦趨，易于學生操作，有益于教學生學會學習，今后遇到類似問題，學生也會類似地解決；其三，注重知識的前后聯(lián)系，其后教師的提問“當α為任意角時，公式還成立嗎？”為誘導(dǎo)公式的理解、記憶做好了鋪墊.

我們知道，鋪墊有益于學生的理解，但不利于培養(yǎng)學生的思維；跳躍思維不利于學生的理解，但能促使學生思考，培養(yǎng)他們的思維. 限時的課堂教學實踐表明：教學需要一定的鋪墊.因此，要求教師基于學情，把握好鋪墊的度，而這個鋪墊（即導(dǎo)入）是教師譜寫優(yōu)美教學樂章的前奏，是師生情感共鳴的第一個音符，也是課堂教學藝術(shù)的重要組成部分. 著名特級教師于漪曾說過：“課的第一錘要敲在學生的心靈上激發(fā)他們思維的火花，就像磁石一樣把學生牢牢吸住.” 由此可見，導(dǎo)入對于一堂課的成功與否非常重要，所以我們要重視課堂的導(dǎo)入.