高中數學核心概念及其教學策略探究

雷蕾

[摘 要] 數學概念是數學學科課程內容的基本組成要素，處于學科的中心位置，對于學生學習數學知識具有重要的支撐作用. 本文在分析數學核心概念的內涵和特征的基礎上，提出了一些高中數學核心概念教學策略.

[關鍵詞] 高中數學；核心概念；內涵；策略

隨著近幾年數學改革越來越多元化，高中數學概念教學越來越被重視，尤其是處于連接知識與知識，構成知識體系的核心概念教學更是受到極大的重視. 高中課程新標準在解讀“核心概念”時也明確指出要重視“核心概念”產生數學思想，學習數學概念是數學基礎. 因此數學教學中教師應以核心概念的構建為突破口，引領學生更加深入地領悟概念，引發心理共鳴，形成內心感悟，從而真正優化學生的認知結構.

[?] 數學核心概念的內涵解讀

數學概念是用高度概括化語言描述研究對象空間和數量關系，具有“內涵和外延”雙重性，所以數學概念具有穩定性和靈活性.

高中數學核心概念就是指高中數學學科的主干知識，能夠形成數學這門學科的所有概念和所有原理的知識. 高中數學概念就是高中數學知識的核心，如函數概念、統計概念以及導數概念等，始終作為高中數學概念的核心貫穿教材始終，并將主導高中數學的思想形式（如數形結合思想、空間思想、統計學思想等）. 但是還有學者認為，核心概念就是一種即使忘掉其基礎信息或者次要信息，但依舊能被廣泛應用的陳述性知識. 又或者將那些早已經超越高中數學教學的，并且會隨著時間變化而不會改變價值的概念叫作核心概念.

[?] 高中數學核心概念的特征

1. 高中數學核心概念具有基礎性

核心概念將數學思想貫穿整個數學知識體系，這對于整個數學學科的發展都具有基礎性. 其余概念也是因它而生，所以體現其核心性. 例如，函數概念不僅可以延伸出奇偶性，還有周期性、單調性，一次函數、二次函數、指數函數、對數函數等，這些概念的基礎都是“函數”概念，所以很好地體現出了核心概念的基礎性.

2. 高中數學核心概念要具有聯系性

高中數學核心概念就是能將普通的一般概念聯系在一起的“組織者”，這也體現了核心概念與概念的關系. 例如，在三角函數中，“三角函數”概念就是核心概念，以它為基礎，能夠推出單調性、函數圖形、弧度制、三角函數性質、三角函數應用、誘導公式等一切基礎概念，這就是起到核心概念的“聯系性”.

3. 高中數學核心概念具有豐富性

通過對核心概念的描述得知，核心概念是非常豐富的概念，其包含的內容非常多，這不是一個簡單的概念所能比擬的，其作為一個基礎概念，自然會涉及多個下位概念，其所體現的數學思想也是無窮無盡的，異常豐富，甚至還存在于其他學科交叉的現象，所以其豐富性很強. 例如，對于一個以原點為中心，2為半徑的圓，通過“集合”概念，可以表示為P={（x，y）∈R

x2+y2=4}，這就體現出集合的豐富性，準確用P={x

p（x）}來表達所以具備P性質的點，這讓整個概括更加整齊，更具有研究的價值.

[?] 高中數學核心概念教學策略分析

通過對高中核心概念的分析和認識，加強教師對核心概念的理解和教學，做好學生對核心概念問題的掌握，擴大學生的思維方式.

1. 對于核心概念要加強理解推導過程

在核心概念的推導過程中學生往往會出現理解不透徹的現象，并且很容易將核心概念與一般概念弄混淆，所以在核心概念教學策略中，首先要指導學生對核心概念的理解和認識，注重其推導過程，這才是核心概念被學生掌握和利用的基本要求. 例如，在“三角函數”核心概念中，要掌握其兩角和差公式，但是這套公式本身比較復雜，而且推導過程也比較麻煩，所以很容易造成學生在研究和使用中不注重對其推導過程加以理解，只會“死記硬背”，經常出現錯誤. 教師需要幫助學生演示該過程的推算規律和三角函數的運算法則，在對二倍角和和差公式的推算中加強學生對于核心概念的理解和產生思維方法，并促進計算. 例如，在“sin145°sin205°+ sin245°sin335°”的解答過程中需要對兩組計算進行變形，通過正余弦變化、和差公式的推導、余弦公式，最終結合誘導公式導出結果. 這道例題就充分展示了對核心公式的推導與演示，讓學生在正余弦公式、兩角和差公式的演示推算中理解和把握核心概念的推導，進一步解決問題.

2. 充分利用概念二重性的性質

高中數學核心概念也是要遵守概念的二重性，即概念既可以是整個過程，也可以是被認知的對象，所以可以借助二重性來解決核心概念的教學.

（1）通過過程化的概念，解決概念的認知

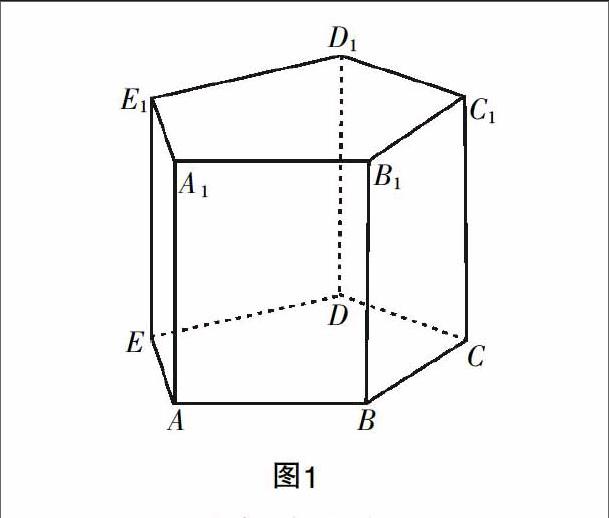
由于核心概念在認識上比較抽象，于是在認知過程中可以先通過過程來理解核心概念，然后再將其放置在被研究的對象上，增加學生理解的過程，不只是記住概念，而且還要形成良好的思維方式. 例如，在“立體幾何”核心概念的理解中，學生先通過對“立體幾何”的描述來理解概念，但是可能還是不完善，于是教師可以借助多媒體將“立體幾何”圖像投影在黑板上，學生自然在研究過程中就掌握了“立體幾何”的概念，彌補描述的不足. 再如，在幾何圖形的“棱柱”概念的教學中，可能學生對“棱柱”概念認知不熟悉，但是可以借助“棱柱”的幾何圖形解釋的過程來解釋不同的“棱柱”概念. 學生先將“棱柱”的概念從字面上進行理解，看看能理解到什么程度，緊接著教師將圖1投射到幕布上，學生看見圖形，再結合棱柱的概念，然后通過添加不同的條件，如添加“棱AA1垂直于底面ABCDE”，那么這個棱柱就變成了“直棱柱”；又或者加上“底面ABCDE是正多邊形”，那么通過過程變化，形成了“正棱柱”的概念. 所以正是不同的過程變化，導致出現不同的“棱柱”的概念，幫助學生熟練掌握.

（2）反思進步，實踐驗證

在核心概念教學中要善于反思，總結學生認識的不足，并組織學生進行實踐驗證. 例如，在學習“空間點線面”后，要結合生活，觀察概念學習是否準確，利用教室中的桌椅板凳來實踐，通過其位置進一步認識核心概念的定義.

學生對于核心概念的理解不是一朝一夕的，而是需要反復漸進，并長期堅持，最終才能加深理解，所以教師要在這個過程中不斷重復核心概念，利于學生記憶.

3. 概念非形式化的合理使用

如果學生能夠通過自己的描述準確反映核心概念的內容，那么會對概念的教學大有裨益. 在教學概念之前，可以組織學生先通過自己探索將核心概念用非形式化的語言表達出來，然后教師再組織學生驗證和修改核心概念的“描述”. 例如，在“一元二次函數”概念教學中，教師通過對“一元一次方程”和“一元一次函數”解讀，指導學生對比“一元二次方程”與“一元二次函數”，學生自己探索認知的概念最牢靠，也便于學生打開思維，提升解決問題的能力.

4. 充分應用，全面掌握核心概念

對于高中數學核心概念的應用是掌握核心概念的關鍵，概念在認知中會經歷“模糊—具體”的變化，而教學過程是“模糊”過程，但是應用概念的過程卻是比較清晰的過程，所以高中數學教師要加強學生對數學概念的應用，然后進一步深刻地理解和把握核心概念. 例如，在二次函數概念講解完畢后，教師可以運用函數例題來檢驗學生的掌握情況：求f（x）=x2-2x-3在區間[2，a-3]上的最小值. 這道題要根據二次函數的概念，并結合參數討論求解. f（x）=x2-2x-3=（x-1）2-4，根據二次函數的概念畫出函數曲線（如圖2）.

當x=1時， f（x）可以取得最小值-4，那么依據二次函數的概念，可以對a-3進行參數討論，最終確定在區間[2，a-3]上求函數的最值問題. 本題就是通過對二次函數概念的靈活運用，展示學生對概念的理解能力和水平，從而讓學生更好地掌握數學的核心概念.

總之，數學概念是數學學科課程內容的基本組成要素，對于學生學習數學知識具有重要的支撐作用. 掌握核心概念，也是高中學生學好數學的關鍵. 因此，在高中數學概念教學中，教師應以核心概念的構建為突破口，用科學的方法研究核心概念理論，并指導核心概念教學實踐，使學生在親歷構建概念、運用概念的過程中，實現對概念的透徹理解，主動地進行知識建構和意義學習.