關于水輪轉動問題教學幾個困惑的探究

譚圓之

[摘 要] 水輪轉動問題是一個典型的三角函數模型的應用問題，轉動水輪上的質點所做的簡諧運動實際上就是在原地打轉，根本就沒有“走”，既然原地打轉，三角函數圖像卻可以跑得很遠.教學中，利用任意角的三角函數定義很自然地研究質點運動與時間的函數關系，利用單位圓的正弦線作正弦函數圖像形成過程建立兩者之間的聯系，在實際圖形與三角函數圖像之間需要建立一種默契和信任.

[關鍵詞] 水輪轉動；三角函數模型；教學困惑

水輪轉動的問題在蘇教版教材作為例題、習題多次出現，而在調研試卷中也時隱時現. 但是作為簡單的簡諧運動，在數學中應用三角函數圖像來研究水輪所做的圓周運動，尤其是高三文科班學生，理解起來還是有一定的距離. 今再次審視這部分內容，感觸頗深.

[?] 課本例題再現

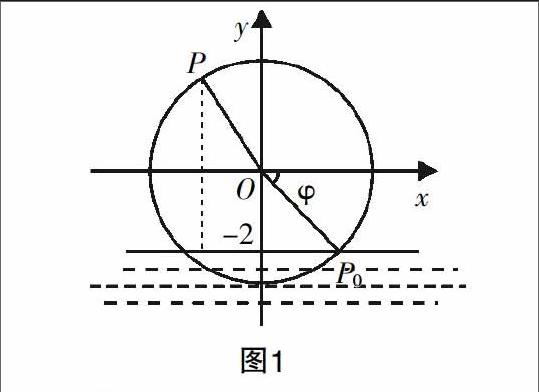
蘇教版教材必修4第43頁例2：一個半徑為3 m的水輪如圖1所示，水輪圓心O距離水面2 m，已知水輪每分鐘轉動4圈，如果當水輪上的點P從水面浮現時（圖中點P0）開始計算時間.

（1）將點P距離水面的高度z（m）表示為時間t（s）的函數？

（2）點P第一次到達最高點大約要多少時間？

事實上在這個例題之前的例1，是研究簡諧運動的物體對平衡位置的位移x與時間t之間的函數關系，其與三角函數圖像更貼近，而本題是一個有關圓周運動的問題，研究圓周運動的點距離平衡位置的高度與時間t之間的函數關系，它與三角函數圖像的聯系，從表面上看僅僅在于動點P相對x軸上下呈現周期性出現，因此兩者聯系起來在教學實踐中顯得稍微抽象些，尤其隨著新課學習時間的流逝，特別是進入高三以后，在遇到這種類型的問題，總感覺牽強得很.

[?] 為什么水輪轉動的問題可以抽象成三角函數模型

在教學實踐中，筆者曾經嘗試過利用物理概念解釋，也嘗試過用任意角的三角函數的定義等兩種策略.

1. 物理知識解釋說

在我們的印象中，三角函數是典型的周期函數，而水輪轉動恰好也是周期運動的，從這一點上看，水輪轉動和三角函數有相似之處，把水輪轉動的數學模型抽象成三角函數具有一定的合理性，因此我國的高中物理新教材教師用書中說：凡符合正弦或余弦變化的運動，都叫簡諧運動. 由此看來，簡諧運動是被烙上正弦函數模型的烙印了，所以理科班的學生理解起來困難不太大，而對于物理不是很精通的文科班學生就難說了.

為了讓學生能夠在自己的最近發展區里尋找到一點物理的味道，教學實踐中筆者翻查了物理書中相關概念，嘗試讓文科班學生能形成一種認同感.

（1）圓周運動：一個做勻速圓周運動的物體在一條直徑上的投影所做的運動即為簡諧運動；

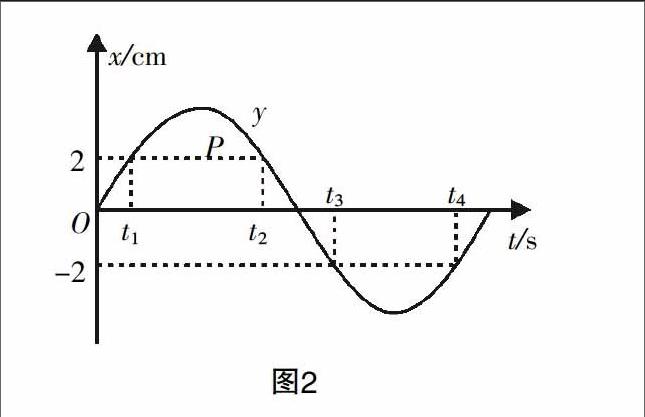
（2）簡諧運動：如圖2，如果質點的位移是隨時間按正弦函數的規律變化的，即它的振動圖像（x-t圖像）是一條正弦曲線，這樣的振動叫簡諧運動. 由此可見，上述例題水輪所做的圓周運動中，點P距離與水面平行的那條直徑的位移，也就是包含正負號的高度的變換，就完全符合簡諧運動的特征，水輪上的點P的位移隨時間，就應該按照正弦函數的規律變化，即它的振動圖像（x-t圖像）是一條正弦曲線.

2. 任意角的三角函數定義說

在教學中，筆者嘗試先搭建幾個臺階：

（1）當水輪上的點P從水平直徑右端點開始計時，在t s內所轉過的角為θ，試求出點P距離水直徑的高度y表示為θ的函數.

（2）當水輪上的點P從豎直直徑上端開始計時，在t s內所轉過的角為θ，試求出點P距離水直徑的高度y表示為θ的函數.

（3）當水輪上的點P從豎直直徑下端開始計，在t s內所轉過的角為θ，試求出點P距離水直徑的高度y表示為θ的函數.

（4）當水輪上的點P從水平直徑右端點開始計時，在t s內所轉過的角為θ，試求出點P距離水直徑的高度y表示為時間t（s）函數.

（5）當水輪上的點P從剛浮出水面開始計時，在t s內所轉過的角為θ，試求出點P距離水直徑的高度y表示為時間t（s）函數.

[?] 水輪轉動中質點“運動實圖”與三角函數圖像怎樣建立函數關系

水輪轉動時，質點所做的簡諧運動實際上就是在原地打轉，根本就沒有“走”，它每次偏離平衡位置最遠不超過振幅，而且也永遠逃不出振幅畫定的圈圈之外. 但是，不少學生就是搞不明白，既然原地打轉，為什么三角函數圖像卻可以跑得很遠？于是糾結而不能自拔. 除了利用任意角的三角函數定義很自然地研究質點運動與時間的函數關系，教學實踐中筆者也嘗試利用單位圓的正弦線作正弦函數圖像形成過程建立兩者之間的聯系.

只要稍微回憶一下單位圓作三角函數圖像，我們不難想象作圓周運動的質點離開水平線的位移，實質上就是單位圓正弦線上以相應角度為該運動時刻所對應的位移. 明白這個道理，不難理解圓周運動的質點的“運動實圖”可以類比單位圓，只不過“運動實圖”的半徑不一定是1個單位，進而理解“運動實圖”模擬正、余弦函數圖像. 我們就拿前面的五個臺階來討論這個話題：

（1）當水輪上的點P從水平直徑右端點開始計時，時間為0，位移也是0，就是說三角函數圖像過（0，0），之后位移增大，這是標準的正弦函數y=Asinθ圖像；

（2）當水輪上的點P從豎直直徑上端開始計時，時間為0，位移也是A，就是說三角函數圖像過（0，A），之后位移減小，這是標準的余弦函數y=Acosθ圖像；

（3）當水輪上的點P從豎直直徑下端開始計時，時間為0，位移也是-A，就是說三角函數圖像過（0，-A），之后位移增大，這是函數y=-Acosθ圖像；

可見，我們只需要根據質點旋轉角終邊位置高度為縱坐標，以計時時間為橫坐標，確定對應三角函數圖像上的點，比如將水輪上的點P初始位置看作正弦函數圖像上的一個特殊點，再加上圓周運動的周期，最后可以利用代點法不難求出函數的解析式.

[?] 水輪轉動計時的不同，對正弦函數y=Asin（ωt+φ）的哪些量有影響

水輪轉動計時開始的時間就是轉動時間t=0的時刻，那么它直接決定了函數圖像與y軸的交點的位置，相當于三角函數圖像開始的位置，那么t=0的時刻就可以得到圖像的一個點的坐標. 同時，根據水輪轉動的方向和點P位移的增減，還可以判斷函數圖像的變換趨勢.

可見，水輪轉動計時開始的時間就是轉動時間t=0的時刻，由t=0的時刻可以得到圖像的一個點的坐標，再用代點法可以求出變量φ，而其他基本量沒有形成直接影響. 當然至此我們也能獲得振幅、角速度、周期、初相位等概念在圓周運動中的實際意義：振幅是振動物體離開平衡位置的最大距離，在圓周運動中，R是勻速圓周運動的半徑；角速度ω是勻速圓周運動的單位時間內所旋轉的角度；周期是做簡諧運動的物體完成一次全振動所需要的時間，也就是轉動一周的時間；初相位φ是t=0時勻速圓周運動的物體偏離該直徑的角度（逆時針為正方向）.

[?] 點P距離水面的高度與到水面的距離有何區別

教學中，部分學生對于例題中高度是否需要加絕對值，總要糾結一番. 其實，高度的概念，和在學生剛剛認識負數的時候接觸到的海拔高度的概念、溫度的度數等概念一樣，本身應該有正負之分，也就是說在水面上方為正，下方為負，這一點在題目中不像單擺運動、質點簡諧振動那樣要規定哪個方向為正.但是只要研究距離，當然應該是高度或者位移的絕對值.

[?] 水輪轉動問題動點P相對的平衡為何總是指向水平直徑而簡諧運動卻選點

在教學中，我們也會不自覺地產生一種莫名的疑惑，為什么水輪轉動問題總是研究P到水平直徑的高度或者位移？動點P到水輪的任一條直徑的位移都是一種三角函數模型，但是我們經常要研究動點到水面的高度的變化規律，所以把水平直徑作為平衡才具有現實意義.

試問，為何不選擇軸心作平衡位置？這個問題很簡單，因為水輪上的點P到軸心距離不變，研究它干什么？當然這并不意味著“點”不可以作為平衡位置.

案例3 如圖4所示，點O為做簡諧運動的物體的平衡位置，取向右的方向為物體位移的正方向，若已知振幅為3 cm，周期為3 s，且物體向右運動到平衡位置最遠處時開始計時.

評注：本題屬于質子振動問題，也可以仿效水輪轉動問題研究，除了不能直接在實物圖上簡歷直角坐標系，只能利用待定系數法. 題中物體向右運動到平衡位置最遠處時開始計時，實際上說明正弦函數圖像經過點（0，3），這是求φ的關鍵條件.當然本題既然知道三角函數圖像的這一特征，實際上我們在設函數時也可以直接設y=Acos（ωt）.