解析幾何學(xué)習(xí)困難因素分析與對(duì)策

徐立

[摘 要] 解析幾何是中學(xué)數(shù)學(xué)的重點(diǎn)和難點(diǎn)，學(xué)生在學(xué)習(xí)解析幾何中遇到學(xué)習(xí)困難的因素是多方面的，引導(dǎo)學(xué)生解決解析幾何學(xué)習(xí)中的困難，是提高其圓錐曲線問(wèn)題解決能力的關(guān)鍵.

[關(guān)鍵詞] 解析幾何；數(shù)學(xué)；困難；因素；對(duì)策；雙曲線；概念；性質(zhì)

解析幾何是高中數(shù)學(xué)知識(shí)體系中非常重要的一塊內(nèi)容，是提高學(xué)生的數(shù)形結(jié)合能力、運(yùn)算求解能力、數(shù)據(jù)處理能力的重要載體之一. 在教學(xué)的過(guò)程中，通過(guò)不同曲線的教學(xué)，讓學(xué)生能從直觀入手，歸納總結(jié)出不同曲線的幾何性質(zhì)，并能用通過(guò)代數(shù)運(yùn)算或結(jié)合幾何性質(zhì)來(lái)解決相應(yīng)的解析幾何問(wèn)題. 但是在學(xué)生學(xué)習(xí)解析幾何的過(guò)程中存在著很多困難，教師也在不斷地改進(jìn)解析幾何的教學(xué)過(guò)程，如何提高學(xué)生學(xué)習(xí)有效性，如何提高教師教學(xué)有效性，是值得深入研究的.

一方面是學(xué)生的學(xué)習(xí)過(guò)程中，學(xué)生感覺(jué)解決解析幾何問(wèn)題時(shí)的方法選擇上比較單一、模式化，計(jì)算錯(cuò)誤頻現(xiàn)，做題積極性不高；另一方面教師在教學(xué)的過(guò)程中，如何才能找到學(xué)生的“最近發(fā)展區(qū)”，讓學(xué)生在已有的知識(shí)和能力的基礎(chǔ)上，更好地體會(huì)和探究解析幾何問(wèn)題解決的一般解題規(guī)律，探尋解析幾何的本質(zhì)，這也是教師需要思考的問(wèn)題.

[?] 問(wèn)題的歸因與分析

造成學(xué)生解析幾何學(xué)習(xí)困難的成因是多方面的，主觀方面有學(xué)生學(xué)習(xí)的方法、思維以及心理等原因，客觀方面有教師在教學(xué)中存在的一些問(wèn)題.原因分析如下：

1. 初中平面幾何教學(xué)與高中解析幾何教學(xué)的銜接不協(xié)調(diào)

學(xué)生在初中階段學(xué)習(xí)平面幾何的時(shí)候，一方面對(duì)于剛剛接觸幾何的初中來(lái)說(shuō)，幾何方面的知識(shí)儲(chǔ)備是非常少的，另一方面學(xué)生的生理成長(zhǎng)階段決定了他們還沒(méi)有達(dá)到一個(gè)很高的抽象概括和邏輯思維能力水平，也認(rèn)識(shí)不到抽象出來(lái)的概念之間存在的內(nèi)在關(guān)系，而推理是建立在對(duì)概念的理解上的，因此很多學(xué)生并不適應(yīng)嚴(yán)密的推理過(guò)程和形式.尤其是初中新課程實(shí)施以來(lái)對(duì)平面幾何教學(xué)要求的降低，“三段論”推理教學(xué)沒(méi)有很好落實(shí). 使得學(xué)生往往重于結(jié)果，輕推理過(guò)程.學(xué)生平面幾何知識(shí)的匱乏，邏輯能力不高，導(dǎo)致解析幾何學(xué)習(xí)困難加大.

2. 解析幾何概念性質(zhì)存在理解困難

直線中傾斜角與斜率的相關(guān)概念聯(lián)系，直線和圓、兩圓位置關(guān)系，橢圓、雙曲線、拋物線的第一定義、性質(zhì)等等對(duì)于學(xué)生而言難度較大，其內(nèi)容本身比較困難，形式化程度較高，對(duì)于學(xué)生的理解存在障礙.

3. 學(xué)生運(yùn)算能力的不足以及對(duì)于運(yùn)算存在的心理障礙

計(jì)算器在初中教學(xué)中的應(yīng)用，降低了對(duì)學(xué)生運(yùn)算能力的要求，導(dǎo)致學(xué)生對(duì)基本的數(shù)字運(yùn)算普遍能力不高. 初中數(shù)學(xué)對(duì)字母運(yùn)算和因式分解教學(xué)要求降低，導(dǎo)致學(xué)生在解析幾何學(xué)習(xí)時(shí)對(duì)于字母運(yùn)算和變形化簡(jiǎn)顯得力不從心. 即使是解決的方法已經(jīng)找到，還是不能將問(wèn)題的解決進(jìn)行到底. 一方面在運(yùn)算的過(guò)程頻頻出錯(cuò)，到處碰壁；另一方面是學(xué)生對(duì)于比較煩瑣的數(shù)學(xué)運(yùn)算存在心理障礙，或不愿意算下去，或?qū)\(yùn)算失去了信心，主動(dòng)放棄.

4. 教師在教學(xué)過(guò)程中存在的一些問(wèn)題

一方面教師在教學(xué)過(guò)程中偏重解題策略的尋找，輕視學(xué)生計(jì)算方法的引導(dǎo)，將許多計(jì)算步驟跳過(guò)，美其名曰讓學(xué)生自己去算，其實(shí)學(xué)生根本沒(méi)算，問(wèn)題不斷積累；另一方面在課堂教學(xué)中留給學(xué)生思考、交流的時(shí)間不夠.再加之一種“問(wèn)題模式化”的教學(xué)方式，影響了學(xué)生學(xué)習(xí)能力的提高.

[?] 案例剖析與對(duì)策

1. 概念教學(xué)

圓錐曲線的概念有很多種定義，中學(xué)數(shù)學(xué)中一般有三種. 第一種是教材中的第一定義，第二種是傳統(tǒng)教材中的統(tǒng)一第二定義，第三種是教材章頭圖中的介紹.從教學(xué)來(lái)看，一般教學(xué)僅圍繞第一定義做出了概念的闡述、分析，導(dǎo)致學(xué)生對(duì)橢圓、雙曲線、拋物線的認(rèn)知不足，現(xiàn)階段不少問(wèn)題并不僅僅研究與定義相關(guān)的問(wèn)題，更多的是從數(shù)學(xué)本質(zhì)的角度思考問(wèn)題，因此要全方位地滲透定義教學(xué)是概念教學(xué)的關(guān)鍵. 筆者給出概念全面性的三個(gè)層次問(wèn)題，提升概念學(xué)習(xí)的理解，從而解決概念學(xué)習(xí)的困難.

問(wèn)題1：已知雙曲線-=1（a>0，b>0），右支上一點(diǎn)P（m，n）到左焦點(diǎn)F1和右焦點(diǎn)F2的距離差為12，兩焦點(diǎn)之間的距離為20，求雙曲線標(biāo)準(zhǔn)方程.

問(wèn)題2：已知平面內(nèi)動(dòng)點(diǎn)P（x，y）到定點(diǎn)A（3，0）的距離比上到定直線x=的距離值等于3，求動(dòng)點(diǎn)P（x，y）的軌跡方程，并說(shuō)明其是什么曲線.

問(wèn)題3：AB與平面α所成角為20°，記斜足為B，若點(diǎn)C是位于平面α上的動(dòng)點(diǎn)，且∠CAB=30°，則點(diǎn)C在平面α上的軌跡是______________.

分析1：從問(wèn)題1可以發(fā)現(xiàn)，本題是典型的雙曲線概念的理解和運(yùn)用，學(xué)生通過(guò)第一定義可以清晰地認(rèn)識(shí)雙曲線的實(shí)軸和焦距，這種概念相關(guān)的問(wèn)題屬于第一層次，學(xué)生對(duì)于概念的理解比較到位，這是源于課堂教學(xué)中數(shù)學(xué)實(shí)驗(yàn)“拉鏈運(yùn)動(dòng)”環(huán)節(jié)進(jìn)行的設(shè)計(jì)，從而獲得了良好的解題體驗(yàn).

分析2：?jiǎn)栴}2是對(duì)于第二定義的一種考查，若沒(méi)有第二定義的理解和思考，本題的入手角度自然是以軌跡求解中的直接法，但是其運(yùn)算量比較大，學(xué)生若能從第二定義的角度入手思考，本題的解決具備了更高的理論高度，自然水到渠成.

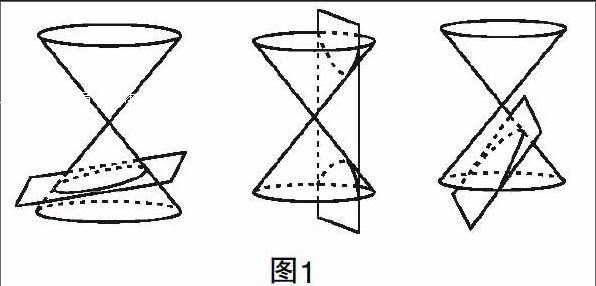
分析3：?jiǎn)栴}3是概念教學(xué)考查的核心. 從圓錐曲線名稱來(lái)說(shuō)，橢圓、雙曲線和拋物線都是有其來(lái)源的. 古希臘數(shù)學(xué)家研究圓錐時(shí)，用不同角度的平面去截取圓錐，從而得到了不同的曲線形態(tài). 如圖，章頭圖很好地闡述了這種變化，教師在教學(xué)中要緊緊地以教材為主，加深概念的思辨性，從而獲得概念教學(xué)的最高層次和境界.

問(wèn)題的解決也比較容易，以AB軸，點(diǎn)C在空間的軌跡恰為圓錐的表面，現(xiàn)截面與軸成20°角，其小于圓錐軸與母線的夾角30°，因此顯然截口曲線是雙曲線.

從上述三個(gè)概念問(wèn)題辨析，對(duì)于概念教學(xué)獲得了層層遞進(jìn)式的理解和運(yùn)用，讓學(xué)生在圓錐曲線概念上的理解得到了進(jìn)一步的提升，只要對(duì)比進(jìn)行問(wèn)題設(shè)計(jì)與嘗試，學(xué)生獲得了全面的概念感知，對(duì)于圓錐曲線概念的學(xué)習(xí)不再是難點(diǎn)，上述以雙曲線為例，橢圓等概念讀者類似可進(jìn)行設(shè)計(jì)教學(xué).

2. 性質(zhì)教學(xué)

圓錐曲線的性質(zhì)比較多，多數(shù)圍繞對(duì)稱性、離心率、位置關(guān)系等進(jìn)行問(wèn)題的設(shè)計(jì). 從學(xué)生學(xué)習(xí)圓錐曲線的性質(zhì)教學(xué)來(lái)看，學(xué)生對(duì)于基本性質(zhì)的認(rèn)識(shí)是了解的，但是并沒(méi)有理解到內(nèi)心深處. 作為教師知道，諸如對(duì)稱性等是橢圓、雙曲線等圖形的基本性質(zhì)，離心率是圓錐曲線統(tǒng)一的性質(zhì). 如何破解有關(guān)性質(zhì)的難題，需要教師合理設(shè)計(jì)問(wèn)題，讓學(xué)生通過(guò)問(wèn)題的解決獲得性質(zhì)使用的感悟.

問(wèn)題5：雙曲線虛軸的一個(gè)端點(diǎn)為M，兩個(gè)焦點(diǎn)為F1，F(xiàn)2，∠F1MF2=120°，則雙曲線的離心率為_(kāi)_____.

分析：離心率研究是雙曲線的重要性質(zhì)的學(xué)習(xí)，關(guān)于離心離的解決主要是從三個(gè)方面入手的. 其一是圓錐曲線定義的使用，其二是平面幾何相關(guān)性質(zhì)的使用，最后是利用點(diǎn)坐標(biāo)方式進(jìn)行運(yùn)算. 學(xué)生最主要的困擾在于后兩種，既無(wú)視平面幾何中諸如三角形正弦定理、余弦定理、角平分線性質(zhì)等使用的不足，又沒(méi)有從運(yùn)算的角度進(jìn)行足夠的計(jì)算，導(dǎo)致離心率問(wèn)題陷入困境. 思考本題不難發(fā)現(xiàn)，可以從平面幾何圖形三角形入手，結(jié)合余弦定理進(jìn)行求解，給出簡(jiǎn)要解答：

總之解析幾何教學(xué)是不折不扣的一個(gè)難點(diǎn)，但是從深入概念本質(zhì)、體會(huì)性質(zhì)的角度做一番獨(dú)到的思辨，有助于教師在后續(xù)教學(xué)中增加教學(xué)的經(jīng)驗(yàn)，將圓錐曲線教學(xué)化繁為易，讓學(xué)生獲得更多的解題體驗(yàn)、快樂(lè). 限于篇幅未能就運(yùn)算方面做出一進(jìn)步的分析，懇請(qǐng)讀者繼續(xù)補(bǔ)充.