基于ANSYS的有限元強(qiáng)度折減法分析邊坡穩(wěn)定安全系數(shù)

何 聰

(重慶交通大學(xué)土木工程學(xué)院 重慶 南岸 400074)

基于ANSYS的有限元強(qiáng)度折減法分析邊坡穩(wěn)定安全系數(shù)

何 聰

(重慶交通大學(xué)土木工程學(xué)院 重慶 南岸 400074)

本文利用有限元強(qiáng)度折減法求邊坡的安全穩(wěn)定系數(shù)。首先介紹了該方法的原理，然后討論各屈服準(zhǔn)則換算以及判斷邊坡失穩(wěn)依據(jù)，最后算例通過有限元強(qiáng)度折減法換算出新的黏聚力和內(nèi)摩擦角輸入ANSYS中進(jìn)行計(jì)算，當(dāng)有限元計(jì)算不收斂時(shí)，此時(shí)的折減系數(shù)作為邊坡的安全穩(wěn)定系數(shù)。

ANSYS;有限元;折減法;安全系數(shù)

一、引言

當(dāng)前，研究邊坡穩(wěn)定性的傳統(tǒng)方法主要有:瑞典條分法，簡(jiǎn)化的畢肖普法等。這些方法主要是建立在極限平衡理論基礎(chǔ)上的，在進(jìn)行穩(wěn)定性分析時(shí)沒有考慮土體內(nèi)部的應(yīng)力應(yīng)變關(guān)系，無(wú)法分析邊坡破壞的發(fā)生和發(fā)展過程，在求安全系數(shù)時(shí)通常需要假定滑動(dòng)面形狀為折線、圓弧、對(duì)數(shù)螺旋線等。而有限單元法不但滿足力的平衡條件，還考慮了材料的應(yīng)力應(yīng)變關(guān)系。求解安全系數(shù)時(shí)，不需要假定滑移面的形狀和位置，也無(wú)需進(jìn)行條分，這使得計(jì)算結(jié)果更加合理精確。有限元法較傳統(tǒng)的方法有如下優(yōu)點(diǎn)：①能夠?qū)哂袕?fù)雜地貌、地質(zhì)的邊坡進(jìn)行計(jì)算；②考慮了土體的非線性彈塑性本構(gòu)關(guān)系，以及變形對(duì)應(yīng)力的影響；③能夠模擬土體的失穩(wěn)過程及其滑移面的形狀。滑移面大致在水平位移突變的地方及塑性變形發(fā)展嚴(yán)重的部位，呈條帶狀；④能夠模擬土體與支護(hù)的共同作用[1]。

二、有限元強(qiáng)度折減法理論

(一)有限元強(qiáng)度折減法的原理

建立在強(qiáng)度折減有限元分析基礎(chǔ)上的邊坡穩(wěn)定分析的基本原理是將邊坡強(qiáng)度參數(shù)黏聚力c和內(nèi)摩擦角φ同時(shí)除以一個(gè)折減系數(shù)F，得到一組新的黏聚力c′和內(nèi)摩擦角φ′[2]。即：

然后作為一組新的材料參數(shù)輸入，再進(jìn)行試算。當(dāng)計(jì)算不收斂時(shí)，對(duì)應(yīng)的折減系數(shù)就是邊坡的安全系數(shù)，此時(shí)，邊坡達(dá)到極限狀態(tài)，發(fā)生剪切破壞，同時(shí)可得到臨界滑動(dòng)面所在的塑性區(qū)。

(二)屈服準(zhǔn)則和流動(dòng)法則的選取

本文計(jì)算采用理想的彈塑性模型。表1是一個(gè)通用的表達(dá)式，通過改變的表達(dá)式就可以在有限元計(jì)算中實(shí)現(xiàn)不同的屈服準(zhǔn)則的轉(zhuǎn)換。是與巖土材料內(nèi)摩擦角φ和黏聚c有關(guān)的常數(shù)。對(duì)于不同的α，k在φ平面上有不同的圓，如圖1，各準(zhǔn)則的α，k在見下表1。

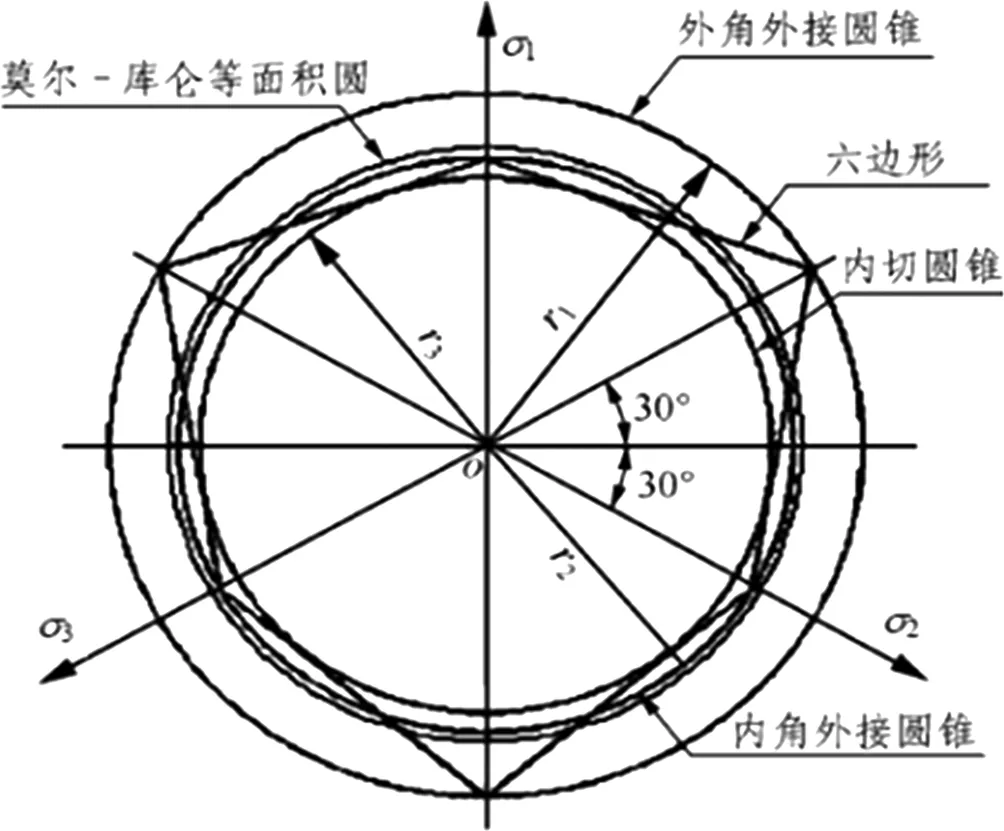
圖1 各屈服準(zhǔn)則在π平面上的曲線

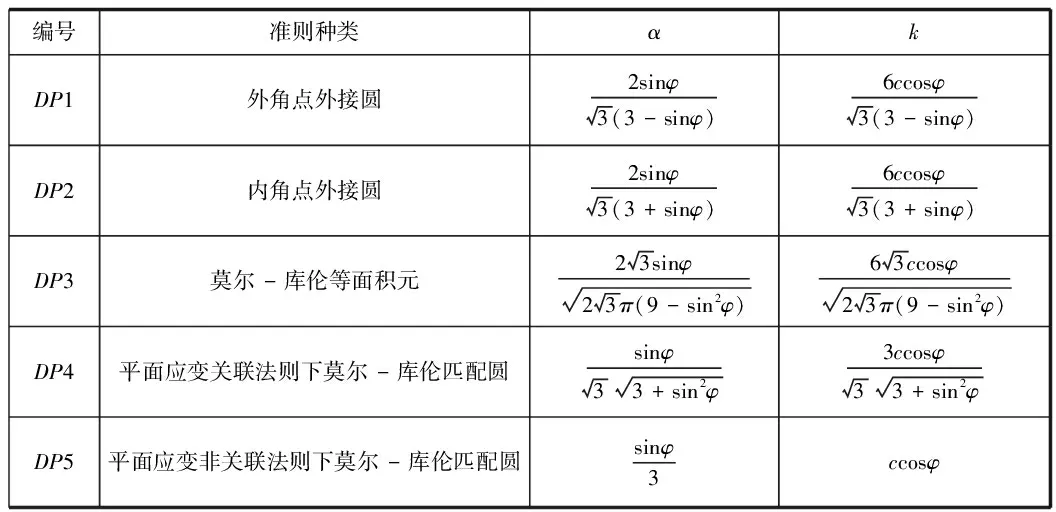
表1 各準(zhǔn)則參數(shù)換算

不同的DP準(zhǔn)則會(huì)得到不同的穩(wěn)定安全系數(shù)，采用外角外接圓DP1屈服準(zhǔn)則與傳統(tǒng)的莫爾庫(kù)倫屈服準(zhǔn)則的計(jì)算結(jié)果有較大出入，不管是評(píng)價(jià)邊坡穩(wěn)定性還是計(jì)算地基極限承載力等，在實(shí)際工程中采用該準(zhǔn)則的安全系數(shù)都偏大，所以是偏于不安全的，因此對(duì)屈服準(zhǔn)則的轉(zhuǎn)換是必要的[3-5]。

(三)邊坡失穩(wěn)判斷依據(jù)

目前，邊坡破壞判斷依據(jù)有如下幾種：①以有限元計(jì)算不收斂時(shí)作為判斷依據(jù)。通常以力或位移的迭代作為邊坡不收斂的判斷依據(jù)。②以廣義的塑性區(qū)從坡腳到坡頂貫通作為邊坡整體失穩(wěn)的標(biāo)志。③土體破壞的標(biāo)志應(yīng)當(dāng)是滑動(dòng)土體無(wú)限移動(dòng)，此時(shí)土體滑移面上應(yīng)變和位移發(fā)生突變且無(wú)限發(fā)展[6]。

三、工程應(yīng)用

(一)計(jì)算模型

某一均質(zhì)土坡，坡高H=20m,坡面傾角β=30°。土容重=20kN/m3，土體彈性模量1×107Pa，泊松比v=0.35，內(nèi)聚力C=42kPa，內(nèi)摩擦角Ф=17°，屈服準(zhǔn)則采用外接圓屈服準(zhǔn)則。計(jì)算按照平面應(yīng)變問題處理，土體用平面單元plane2模擬，兩側(cè)為水平滑動(dòng)支撐，基底采用剛度邊界，上部邊界為自由邊界，網(wǎng)格劃分如圖下。本例中取得折減系數(shù)為1.0,、1.56、1.57三種情況。

圖2 有限元模型

(二)邊坡穩(wěn)定性分析

從以下圖3～圖8分析得出：當(dāng)折減系數(shù)為1.0時(shí)，計(jì)算機(jī)自動(dòng)計(jì)算至收斂，邊坡的x方向位移不大，塑性區(qū)位移不大；隨著折減系數(shù)增加，當(dāng)折減系數(shù)為1.56時(shí)，計(jì)算機(jī)自動(dòng)計(jì)算至收斂，邊坡的x方向位移也隨之增大；當(dāng)折減系數(shù)為1.57時(shí)，計(jì)算不收斂，塑性區(qū)貫通，此時(shí)x方向上的位移值發(fā)生突變，任務(wù)邊坡發(fā)生破壞。所以，邊坡安全安全系數(shù)為1.57。

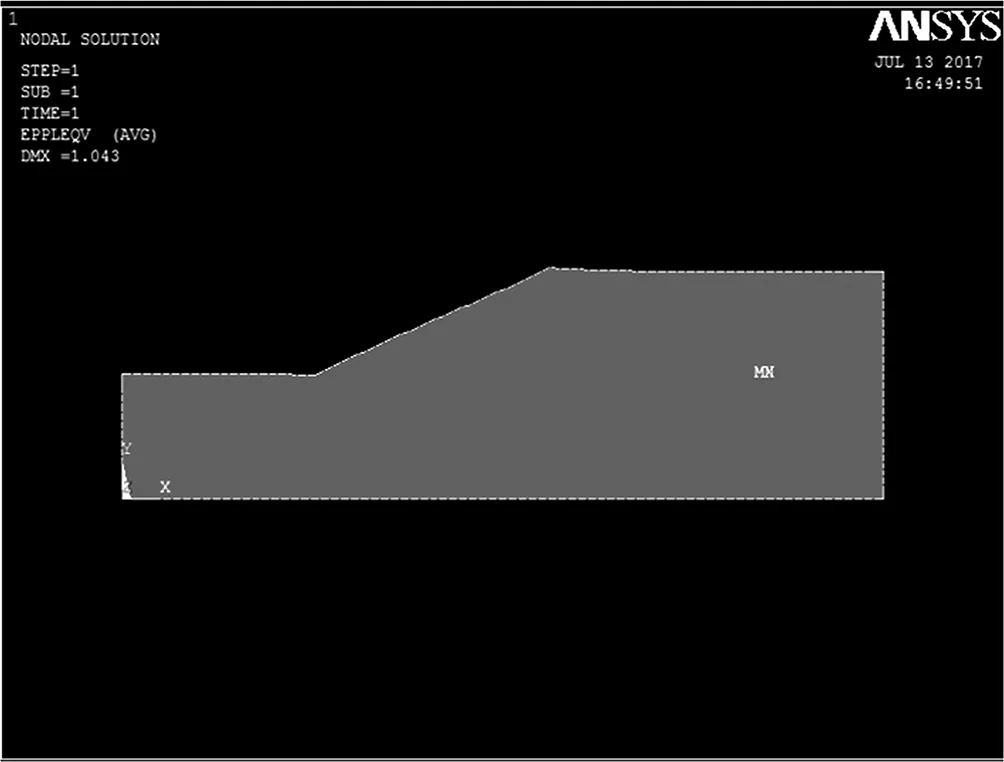
圖3 折減系數(shù)F=1.0X方向等效位移

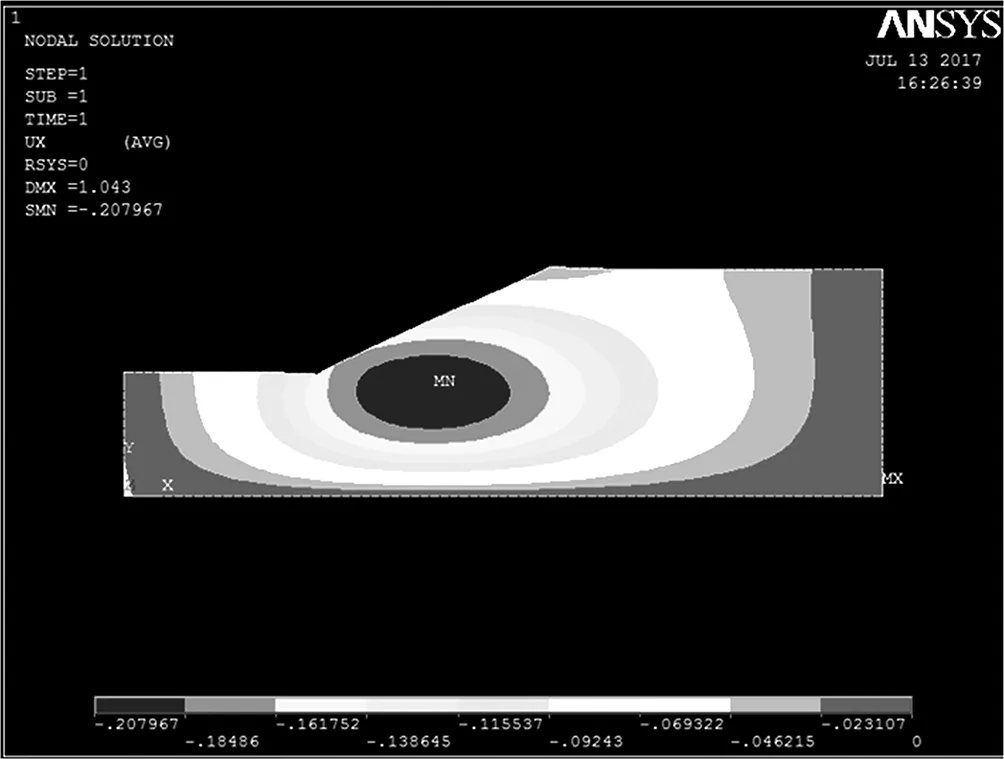
圖4 折減系數(shù)F=1.0等效塑性區(qū)

圖5 折減系數(shù)F=1.56X方向等效位移

圖6 折減系數(shù)F=1.56等效塑性區(qū)

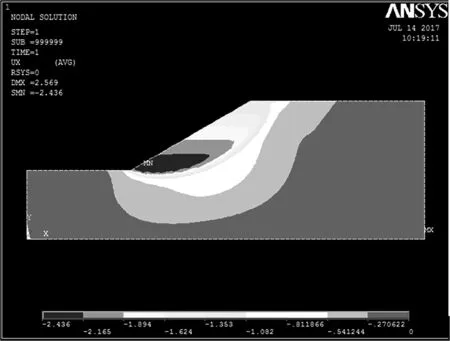
圖7 折減系數(shù)F=1.57X方向等效位移

圖8 折減系數(shù)F=1.57等效塑性區(qū)

四、結(jié)語(yǔ)

通過以上分析，可以得出以下結(jié)論：

1.有限單元法不需要作任何假定，計(jì)算模型不僅滿足力的平衡方程，而且滿足土體的應(yīng)力應(yīng)變關(guān)系，計(jì)算結(jié)果更可靠。該方法能分析各種復(fù)雜形狀的邊坡，不需要假設(shè)滑動(dòng)面。

2.有限單元折減法分析邊坡的穩(wěn)定性，折減系數(shù)本身就是傳統(tǒng)意義上的邊坡穩(wěn)定系數(shù)，通過折減土體材料的強(qiáng)度來(lái)分析邊坡的穩(wěn)定性，直到不收斂，此時(shí)的折減系數(shù)即為邊坡的安全系數(shù)。利用ansys后處理程序可以得出直觀的坡體實(shí)際滑動(dòng)面。

3.通過有限元強(qiáng)度折減，當(dāng)坡體到達(dá)極限狀態(tài)時(shí)，邊坡塑性區(qū)將得到從坡腳到坡頂出現(xiàn)貫通的滑動(dòng)帶。因此塑性區(qū)的貫通可以作為邊坡安全系數(shù)的重要依據(jù)。

在強(qiáng)度折減后得出的位移和變形值不能真正反映邊坡實(shí)際的位移和變形，只是用強(qiáng)度折減法，使得模型計(jì)算不收斂，從而得到邊坡的安全系數(shù)。

[1]趙尚毅，鄭穎人，等.用有限元折減法求邊坡穩(wěn)定安全系數(shù)[J].巖土工程學(xué)報(bào)，2002,24(3)：343-346.

[2]徐干成，鄭穎人.巖土工程中屈服準(zhǔn)則應(yīng)用的研究[J].巖土工程學(xué)報(bào)，1990,12(20):93-99.

[3]李守華.基于不同D—P屈服準(zhǔn)則的邊坡安全系數(shù)比較[J].甘肅科技,2012,28(10):108-109.

[4]陳鵬.公路順層巖質(zhì)邊坡穩(wěn)定及其影響因素分析[D].浙江大學(xué),2012.

[5]高姝妹,李曉寧,馮君.基于有限元強(qiáng)度折減法的土質(zhì)邊坡穩(wěn)定性分析[J].山東工業(yè)技術(shù),2016(14):244-245.

[6]陳琰.巖土邊坡的有限元穩(wěn)定性分析[D].河海大學(xué),2006.

何聰(1990.12-)，男，漢，四川達(dá)州，學(xué)生，碩士研究生，重慶交通大學(xué)，研究方向：隧道與地下工程設(shè)計(jì)。