基于“案例導入式”的統計學教學實踐探討

蔡宏宇

摘要：統計學作為收集、整理和分析數據的方法科學，其統計理論和方法較為枯燥難懂，“案例導入式”教學方法應運而生，本文主要從統計理論、統計方法、統計模型和統計分析四個大的方面闡述“案例導入式”教學方法的運用。

關鍵詞：案例導入式；統計學；教學實踐

統計學則是一門收集、整理和分析數據的方法科學。收集、整理和分析數據需要設計一些項目、確定收集資料的方式和方法、整理和分析數據的原理及技巧。因此，“案例導入式”教學方法實踐主要從統計理論、統計方法、統計模型和統計分析四個大的方面進行闡述，重點介紹統計學中比較難以理解的部分內容，以拋磚引玉。

一、統計理論案例導入式教學實踐

統計學以其嚴密的統計思維、科學的搜集、整理、分析數據信息的理論和方法，成為智慧學、大數據背景下數據科學家的搖籃。沒有統計理論做基礎，統計方法就無章可循。以“統計總體”和“標志”理論為例闡述統計理論案例導入式教學實踐。

1.“統計總體”概念案例導入式教學實踐

日常生活中，我們經常講到“整體”，其實統計學管它叫做“總體”，那么，怎么界定？它具備哪些特征？

案例導入：我們這個班有包括貿易、金融、稅收、財管、會展五個專業、同學們自不同地方、各自興趣愛好不同、政治面貌不同、民族不同、有男女性別之分……，但大家有一點是相同的，那就是大家都選在同一時間和同一個老師一起學習《統計學》，因此組成了一個整體（臨班0437），統計學稱這個整體叫做“統計總體”。

“統計總體”概念和特征導出：“客觀存在的、同一性質基礎上結合起來的許多個別事物的整體”。具備大量性、同質性和差異性的特點。

2.“標志”概念案例導入式教學實踐

統計總體中包括許多個體（總體單位），每一個個體具有不同的屬性特征，即標志。標志其實就是標準、水準、測量依據等等，統計學中的標志定義怎么界定？

案例導入：臨班0437同學按照“性別”標準可以劃分為男同學和女同學；按照“民族”標準可以分為漢族、苗族、維吾爾族和土家族四個民族；按照“年齡”標準可以分為20周歲以下、20至21周歲、21周歲以上三個年齡段。

以上“性別”和“民族”分別說明了臨班0437同學的性別和民族的品質屬性，“年齡”說明了臨班0437同學年齡的數量特征。

“標志”概念導出：“標志是指對客觀現象總體內個體單位的屬性和數量特征進行測量所依據的標準，或用來說明總體單位特征或屬性的名稱。分為品質標志和數量標志，前者不能用數量表現而只能用文字、符號或代碼來說明；后者能用數量表現。

二、統計方法案例導入式教學實踐

統計學中統計方法很多，如集中和離散趨勢測度、時間序列分析測度、統計指數測度、抽樣估計、假設檢驗以及相關和回歸分析測度等。列舉其中幾個學生不容易理解和容易出錯的統計方法實踐案例導入式教學方法。

1.調和平均數案例導入式教學實踐

案例導入：菜場上有1元錢起售的蔬菜，若早上購買每斤0.33元，中午購買每斤0.25元，下班后購買每斤0.2元，試問：早中晚各用1元錢購買的蔬菜平均每斤多少錢？

分析求解：根據算術平均數的定義，計算算術平均數，需要已知變量數列中某數量標志值之和與全部單位總數，題中雖然已知數量標志值之和，但總體單位數未知，然已知每次購買金額和單價，就可以每次購買金額除以每次購買單價得出早中晚三次的購買數量分別為3斤、4斤和5斤，這樣就可以求出平均單價：

總結概括：這種算法是以支出額為權數，以每次購買單價為變量值，以變量值的倒數形式求出平均價格，稱為簡單調和平均數；如果每次購買金額不同，則用每次購買金額為權數進行加權求出平均數： ，這就是加權調和平均數。

上述案例：如果早、中、晚購買的金額分別是1元、2元和3元，則平均價格：

可見，調和平均數是在總體單位數未知的情況下求平均數的一種統計方法，也可以說是算術平均數的一種特例（詳見“統計方法之間推導案例導入式教學實踐”）；簡單調和平均數是加權調和平均數的特例。

調和平均數計算公式導出：調和平均數是各個變量值倒數的算術平均數的倒數。又稱為倒數平均數。用H表示，分為： 簡單調和平均數、加權調和平均數。

（1）簡單調和平均數： （據未分組資料計算）

（2）加權調和平均數： （據分組資料計算）

2.序時平均數案例導入式教學實踐

序時平均數是根據時間序列中各個時期或時點的發展水平即指標值加以平均所得到的平均數。因時間序列可分為絕對指標、相對指標和平均指標時間序列，所以序時平均數可分別不同序列求解。

因時點數列都是瞬間數據，兩個時點之間一般都有一定間隔，因此，時點數列一般都是間斷的。但如果時點數列的資料是逐日記錄，且逐日排列的，這樣的時點數列就可看作是連續的，無論是連續時點數列還是間斷時點數列，都存在間隔相等和間隔不等兩種情況，據此根據時點數列計算序時平均數，有以下四種方法。這里僅以間隔相等間斷時點數列為例闡述案例導入式教學方法實踐。

圖1：時點數列計算序時平均數的四種情形

案例導入：已知某省2016年人口資料如表1，求該省2016年年平均人口數。

表1 某省2016年各季首人口資料

分析求解：已知5個時點數據，每兩個數據之間距離相等，都是三個月，且均為各季首數據，即可先求出各季平均數，然后據各季平均數用簡單平均法求全年平均數：

計算公式導出：時間數列是按間隔相等的時點數編制的，如月末、季末等職工人數、資產額、庫存額等時間數列大都是間隔相等的時點數列；可假定現象在相鄰兩個時點之間的變動是均勻的；則可對相鄰兩個時點求簡單算術平均數；然后將這些平均數相加除以平均數的個數，即為整個數列的序時平均數 ，稱為“簡單序時平均法”或“首末（尾）折半法”。endprint

即

3.統計方法之間推導案例導入式教學實踐

統計方法之間由于已知條件的不同，方法之間可以互相轉化，這里以算術平均數和調和平均數之間互相轉化為例，闡述案例導入式教學方法的應用。

案例導入：菜場上有1元錢起售的蔬菜，若某人早上用1元錢購買了一種蔬菜共3斤，每斤0.33元；中午降價時又買了4斤，每斤0.25元；晚上削價處理時又用1元錢買了5斤，每斤0.2元，試問：某人早中晚各用1元錢購買的蔬菜平均每斤多少錢？

分析求解：上述問題根據不同的資料可用三種方法計算蔬菜的平均價格：

方法1，如已知早中晚各買1元錢，共3元，共計買了12斤菜，可用簡單算術平均法計算平均價格：

方法2，如已知早上買3斤、中午買4斤、傍晚買5斤，又知價格分別為0.33元/斤、0.25元/斤、0.2元/斤，則可用加權算術平均數方法計算平均價格：

方法3，如已知早上買1元錢、中午買1元錢、傍晚也買1元錢，知道每次購買單價分別為0.33元/斤、0.25元/斤、0.2元/斤，但每次購買數量未知，根據加權算術平均數計算公式無法求出蔬菜的平均價格，需先根據每次購買金額和單價求出其數量，即求出平均單價公式的分母，再用總金額除以三次購買的數量之和，求出平均價格：

這種算法是以支出額為權數，每次購買單價為變量值，以變量值的倒數形式求出平均價格，稱為簡單調和平均數；如果每次購買金額不同，則用每次購買金額為權數進行加權求出平均數：

，這種計算平均數的方法稱為加權調和平均數。

上述案例：如果早中晚購買的金額分別是1元、2元和3元，則平均價格：

總結導出：

（1）當權數m1都等于1時， ，可見簡單調和平均數是加權調和平均數的特例；

（2）社會經濟生活中，加權調和平均數，一般作為加權算術平均數的變形之式使用，當m=xf 時，

（3）由相對數或平均數分組資料計算平均數時，若已知分子、分母兩個總量指標時，可直接對比求 ；若已知分母、缺分子資料時，可用加權算術平均法求 ： ；若已知分子、缺分母資料時，可用加權調和平均法求 ： 。可見由相對數或平均數計算的平均數，其實質就是數列的總相對數或總平均數。

三、統計模型案例導入式教學實踐

這里以相關和回歸最小二乘法模型為例，闡述統計模型案例導入法教學方法實踐。

1.最小二乘法模型案例導入

從某高校2012級經濟學專業45名同學中隨機抽取了10位同學，收集到該樣本的高等數學與統計學考試成績資料如表2所示。要求：（1）擬合統計學成績y倚高等數學成績x之間的直線回歸方程，并指出高等數學成績每增加1分時統計學成績如何變化？

表2 高等數學與統計學成績分布表

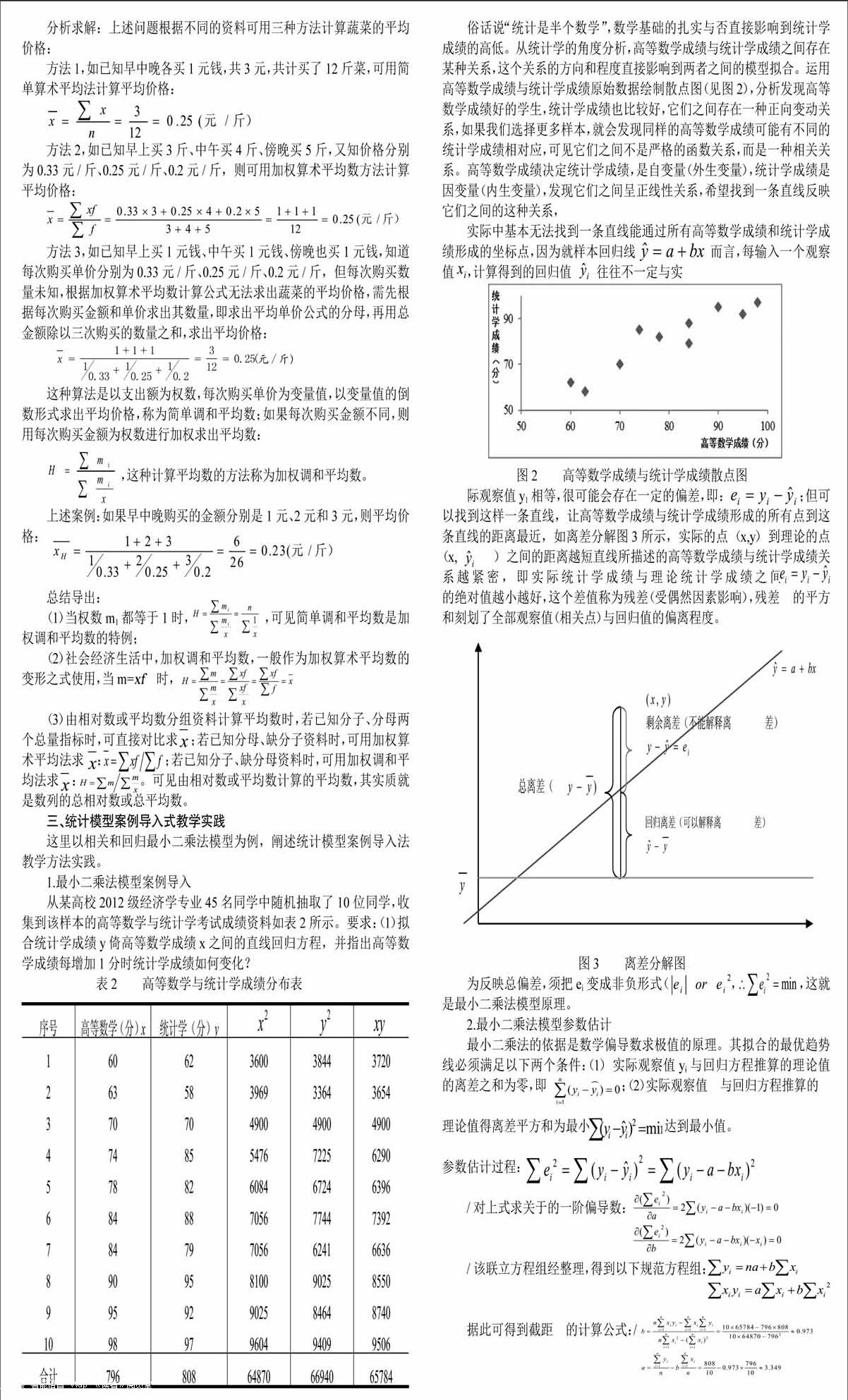
俗話說“統計是半個數學”，數學基礎的扎實與否直接影響到統計學成績的高低。從統計學的角度分析，高等數學成績與統計學成績之間存在某種關系，這個關系的方向和程度直接影響到兩者之間的模型擬合。運用高等數學成績與統計學成績原始數據繪制散點圖（見圖2），分析發現高等數學成績好的學生，統計學成績也比較好，它們之間存在一種正向變動關系，如果我們選擇更多樣本，就會發現同樣的高等數學成績可能有不同的統計學成績相對應，可見它們之間不是嚴格的函數關系，而是一種相關關系。高等數學成績決定統計學成績，是自變量（外生變量），統計學成績是因變量（內生變量），發現它們之間呈正線性關系，希望找到一條直線反映它們之間的這種關系，

實際中基本無法找到一條直線能通過所有高等數學成績和統計學成績形成的坐標點，因為就樣本回歸線 而言，每輸入一個觀察值 ，計算得到的回歸值 往往不一定與實

圖2 高等數學成績與統計學成績散點圖

際觀察值y1相等，很可能會存在一定的偏差，即： ；但可以找到這樣一條直線，讓高等數學成績與統計學成績形成的所有點到這條直線的距離最近，如離差分解圖3所示，實際的點（x，y）到理論的點（x， ）之間的距離越短直線所描述的高等數學成績與統計學成績關系越緊密，即實際統計學成績與理論統計學成績之間的離差 的絕對值越小越好，這個差值稱為殘差（受偶然因素影響），殘差 的平方和刻劃了全部觀察值（相關點）與回歸值的偏離程度。

圖3 離差分解圖

為反映總偏差，須把ei變成非負形式（ ， ，這就是最小二乘法模型原理。

2.最小二乘法模型參數估計

最小二乘法的依據是數學偏導數求極值的原理。其擬合的最優趨勢線必須滿足以下兩個條件：（1）實際觀察值yi與回歸方程推算的理論值 的離差之和為零，即 ；（2）實際觀察值 與回歸方程推算的

理論值得離差平方和為最小 達到最小值。

參數估計過程：

/對上式求關于的一階偏導數：

/該聯立方程組經整理，得到以下規范方程組：

據此可得到截距 的計算公式：/

由此可求得樣本回歸模型： =a+bx

3.最小二乘法模型構建及詮釋

根據案例數據可求得a、b兩個參數：

把相關數據代入模型代入相關數據可得高等數學成績與統計學成績回歸模型： ，可見高等數學成績每增加一個分，統計學成績平均增加0.97分。

四、統計分析案例導入式教學實踐

統計分析方法較多，以統計指數因素分析為例，闡述“案例導入式”教學方法在統計分析中的實踐。

1.因素分析案例導入

如果某公司只銷售三種商品，它們報告期和基期的單價和銷售量如表3。公司經理問：“作為統計員請告訴我報告期我們公司銷售額增加多少？是什么因素引起的？這些因素分別影響多少？”公司數據如表3：endprint

表3 某公司銷售資料

分析表3發現，因各種商品單位不同，無法直接匯總計算；但知道銷售額等于商品單價乘以銷售量，也就是公司銷售額變動受單價和銷售量兩個因素影響，這兩個因素中任何一個變動都會引起銷售額相應變動；顯然，報告期總銷售額除以基期總銷售額，就可計算出報告期發展速度；報告期總銷售額減去基期總銷售額，就可得到報告期銷售額增減額；但這個發展速度和增減額中，有多少是因為銷售量的變動引起的？又有多少是因商品單價變動帶來的？

這是個因計量單位不同引起的無法綜合計算的問題，需要運用綜合指數。從而導出綜合指數的概念和編制。

2.綜合指數編制

（1）綜合指數的概念。綜合指數就是研究不能直接加總的復雜現象的綜合變動程度的相對數，如消費品價格指數、股票價格指數等等。綜合指數的編制需要引進兩個概念：指數化指標和同度量因素。

指數化指標是指數所要測定其變化程度的那個因素。如銷售量指數中的銷售量就是指數化指標；同度量因素是指在編制綜合指數時，將不能直接相加的指數化指標乘上另一個因素，使之可以相加，那個乘上的因素就是同度量因素。如銷售量指數中的價格因素就是同度量因素。

（2）綜合指數的編制原理

①物價綜合指數：綜合說明商品或產品價格綜合變動程度的相對數，是質量指標指數。

為兩個時期的價格，是物價指數要研究的對象，稱為指數化指標； 為報告期物量，作權數，稱為同度量因素。具有以下三個特點：其一，先綜合后對比；其二，計算資料要求較全面；最后，綜合指數分子和分母的差額稱為“影響效果”， 即為價格變動對物值變動的影響額。

②物量綜合指數：說明商品銷量或產品產量綜合變動程度相對數，它是數量指標指數。

：指數化因素； ：同度量因素。

③物值綜合指數：表明物值變動程度的總指數。

相對數：

絕對數：

可見，銷售量和銷售價格兩個因素影響銷售額，分析兩者對銷售額的影響時，在有現實經濟意義的前提下，實現指數體系的成立，可以先假定銷售價格（銷售量）不變，分析銷售量（銷售價格）變動；因社會經濟現象復雜不能直接綜合，需要引進同度量因素，將同度量因素固定以消除同度量因素變動的影響；可見指數編制原則：編制數量指標指數時，其同度量因素固定在基期；編制質量指標指數時，其同度量因素固定在報告期。

（3）綜合指數編制實踐

根據導入案例數據資料，計算得出報告期、基期及假定銷售額數據，如表4：

表4 某公司報告期與基期銷售額數據

根據表4數據，代入綜合指數公式，可求得該公司銷售量、價格指數和銷售額總指數：

解：

分析：該公司銷售額報告期比基期增長89.1%，增加298.4萬元；其中：因銷售量增長19.1%，增加64萬元；因銷售價格上漲58.7%，增加234.4萬元。

參考文獻：

[1]Joan Garfield.Teaching Statistics Using Small-Group Cooperative Learning.Journal of Statistics Education ， 1993，（1）.

[2]J Martin Bland.Teaching statistics to medical students using problem-based learning： the Australian experience. BMC Medical Education BMC series ，2004， （4）

[3]伍亞舟，易東，張彥琦，劉嶺，趙增煒，陳軍..案例教學法在醫學統計學教學中的應用[J].基礎醫學教育，2011，13（7）：635～638.

[4]宋繼華，宋華艷.基于項目驅動的統計學課程教學改革與實踐研究[J].商業經濟，2013，（4）：118～119.endprint