基于多項式擬合的抗干擾慣性系對準算法
胡華峰,劉 明,李 旦
(湖北航天技術研究院總體設計所,武漢 430040)
基于多項式擬合的抗干擾慣性系對準算法
胡華峰,劉 明,李 旦
(湖北航天技術研究院總體設計所,武漢 430040)
針對包含陣風、發動機振動、人員上下車等環境下進行慣性系對準時因慣性器件偏差及外界擾動帶來的比力干擾導致離散化解算對準精度差的問題,在對慣性系對準過程中的參考矢量進行了詳細推導分析的基礎上,提出將多項式擬合應用到慣性系對準中。該算法對整個對準過程中的視速度進行多項式擬合,利用擬合后的視速度代替容易受擾動引起跳變的單周期輸出。仿真及測試結果表明,相比于不進行擬合的傳統方案,該方案能明顯提升對準精度,方位對準精度提高了7倍以上,能方便地進行工程應用,且工程應用效果好。
抗干擾;慣性系;多項式擬合;初始對準
慣性導航系統(INS)中一個十分重要的問題就是其初始對準問題[1]。慣性導航系統的初始對準,是指導航系統尚未進入導航工作狀態之前,確定載體坐標系與導航坐標系之間的關系,為導航計算提供必要的初始條件,因此,慣導系統初始對準的好壞,將直接關系到慣導工作性能的好壞[2]。
傳統固定位置的靜基座粗對準方法是根據陀螺儀對地球自轉角速度的測量值和加速度計對地球重力加速度的測量值來計算出載體的初始姿態矩陣。在實際對準過程中經常受到外界的復雜干擾[3],如陣風、海浪搖擺、發動機振動、人員上下車等擾動環境,車載慣導系統中陀螺儀和加速度計的輸出信號中包含了因載體擺動而產生的誤差信息。如果不及時補償這種誤差,直接采用靜基座粗對準方法進行初始粗對準,將產生較大的粗對準誤差,使系統的精對準時間延長甚至無法進入精對準階段[4]。
目前,為了解決載體在較大幅度晃動下的對準問題,常用慣性系對準方案解決在晃動基座上的對準問題[5-7]。慣性系對準方案對搖擺基座和存在垂蕩、橫蕩、縱蕩或者干擾近似是周期性的干擾時(即在對準時間內通過積分運算,正、負部分能基本抵消)有較好的性能。該方案可以有效地分離載體由于搖擺而產生的加速度干擾,以此達到高精度的對準。法國IXSEA 公司的PHINS 采用的就是基于慣性系的對準方案。
在實際工程應用中,慣性器件偏差及擾動運動的影響會導致加速度計的輸出在慣性系下的投影中存在干擾加速度信息。如何消除干擾的影響得到相對純凈的重力加速度信息是慣性系對準的關鍵所在。有學者提出了頻域內濾波器(IIR 或FIR 低通濾波器)來提取慣性系下參考矢量,從而實現對準的方案[8-9]。文獻[10-11]提出利用小波濾波的方法進行預處理降低器件噪聲,提升對準精度。文獻[12]針對振動干擾的影響,分析了初始導航慣性系下參考矢量的時域特性,提出了參考矢量的最小二乘擬合模型,根據該模型設計了抗干擾重力加速度積分粗對準算法,最后通過仿真驗證了算法的有效性,但未給出詳細的線性表達式、直接的擬合階次分析及工程應用考核。
本文針對工程應用中用離散化方式進行慣性系粗對準時對振動干擾抑制能力差的問題,對慣性系對準過程中的參考矢量進行詳細推導,給出了BI0系(初始捷聯慣導慣性坐標系,0時刻與體系重合)下視速度的線性表達式,并提出采用多項式擬合的方式對進行擬合,利用擬合結果進行對準解算。通過仿真分析及試驗驗證了該算法的有效性。
1 慣性系對準算法
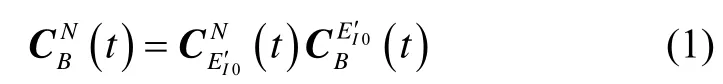
其中:N為導航坐標系;B為載體坐標系;EI′0為初始時刻地球慣性坐標系。在準靜基座情況下:
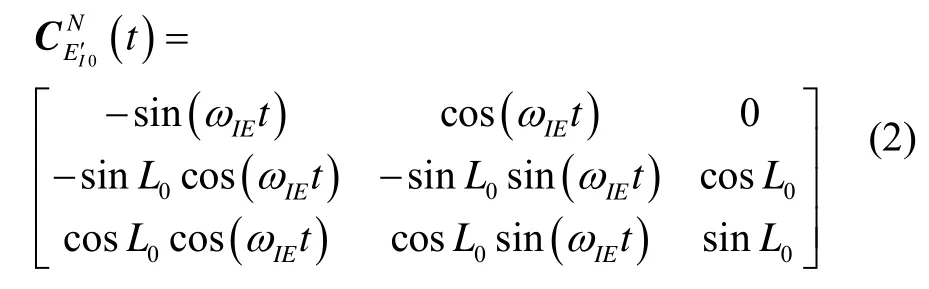
式中:0λ和L0分別為對準起始t0時刻捷聯慣組的經度和緯度。求得矩陣之后,姿態矩陣的實現就轉換為求解為捷聯慣導相對于初始時刻慣性空間的變換矩陣。可將進一步拆寫成:
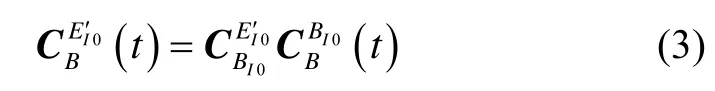
式中:利用陀螺輸出的角運動信息,通過捷聯慣導姿態更新式可以求得矩陣即
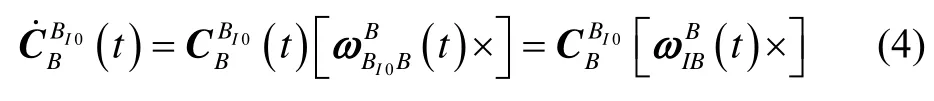
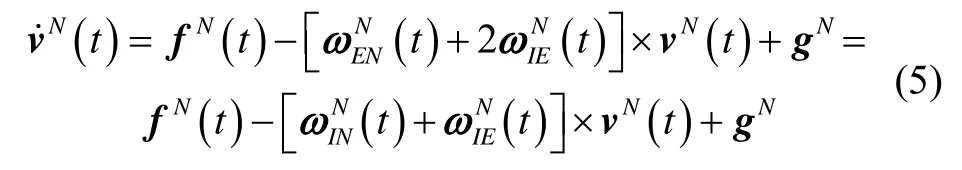
將式(5)改寫如下:
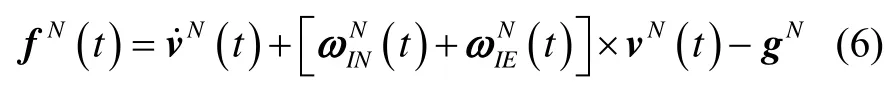
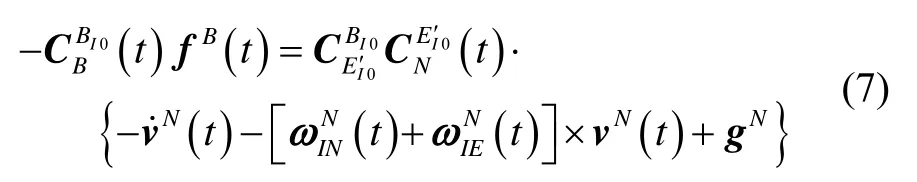
在準靜基座情況下(即載體無對地運動,地速為零),N系對地速度及加速度為零,代入式(7)可得:
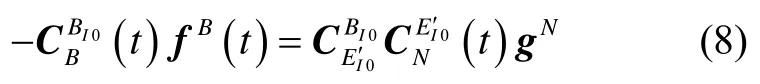
將式(8)兩邊從t0時刻到t時刻同時積分,可得:
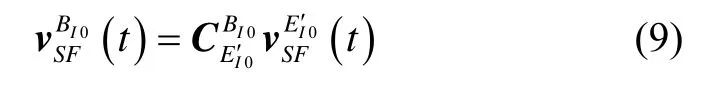
其中:
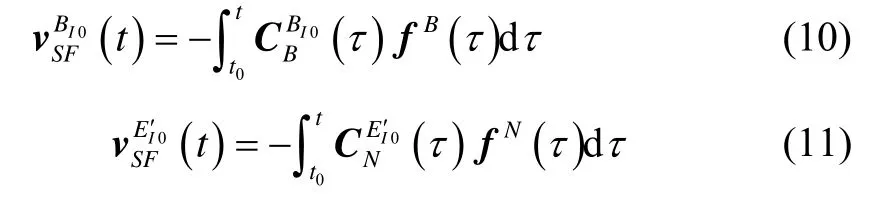
分別取t=t1和t=t2兩個對準過程中的不同時刻,根據矩陣構造算法即可求得常值矩陣即
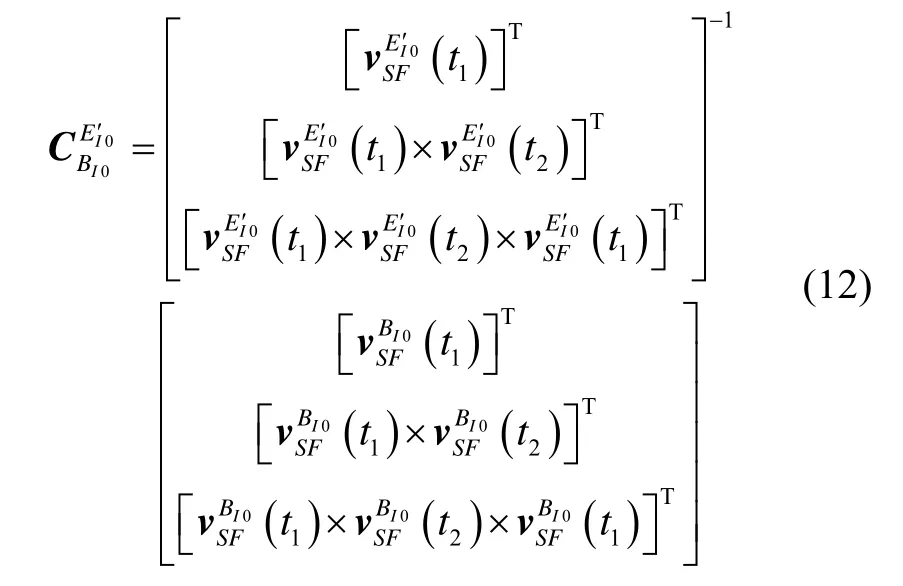
2 多項式擬合平滑視速度
在工程實際應用中,以離散化方式計算BI0系下視速度時,容易因單采樣周期間器件輸出的跳變導致輸出不穩定,影響對準結果。本節研究對進行多項式擬合的方法。由第1節知:
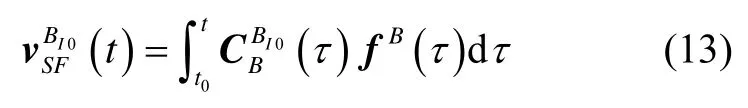
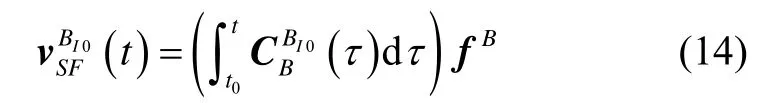
其中:
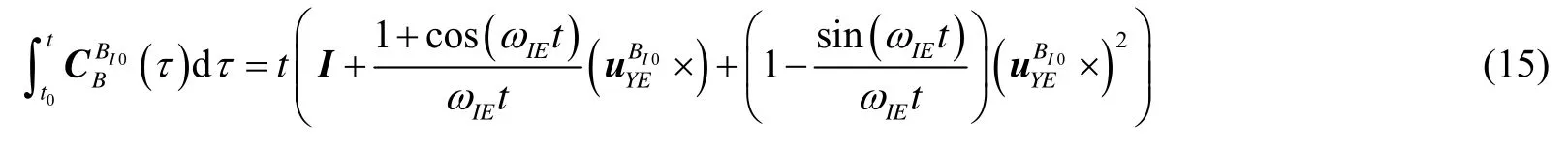
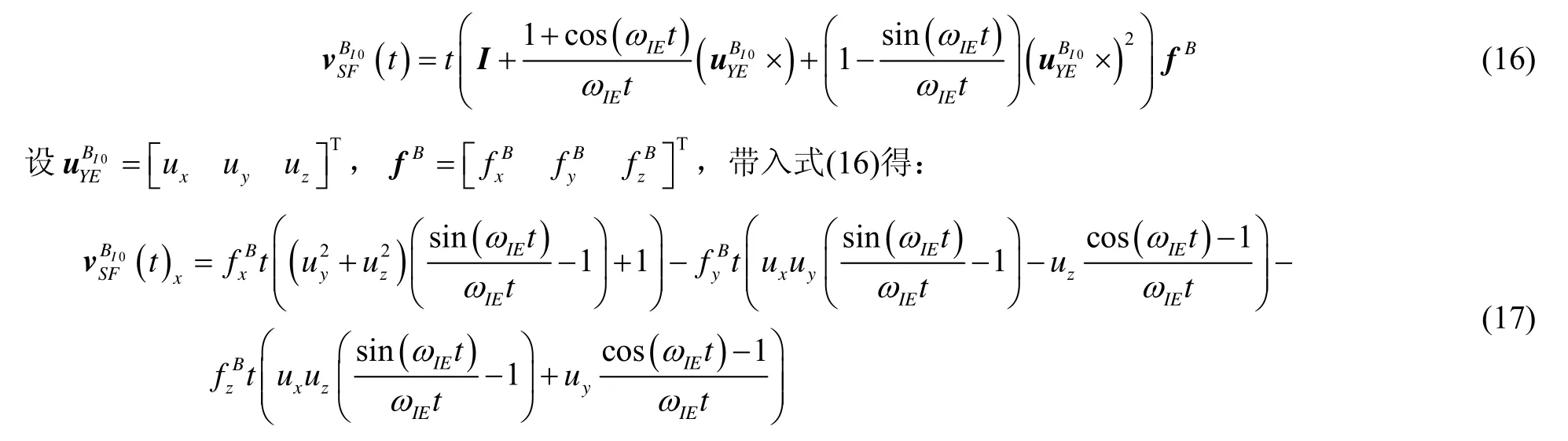
考慮對準時間一般較短,ωIEt為小量,忽略三階及以上項,有:
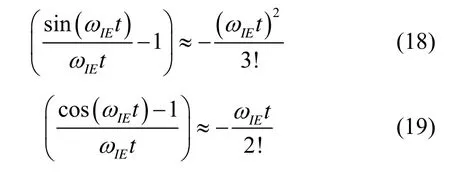
因此式(17)可以簡化為
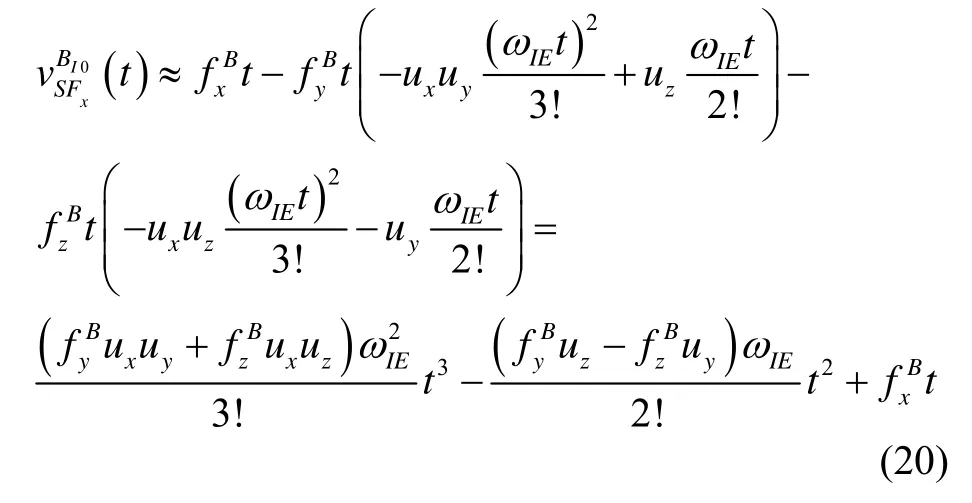
同理,
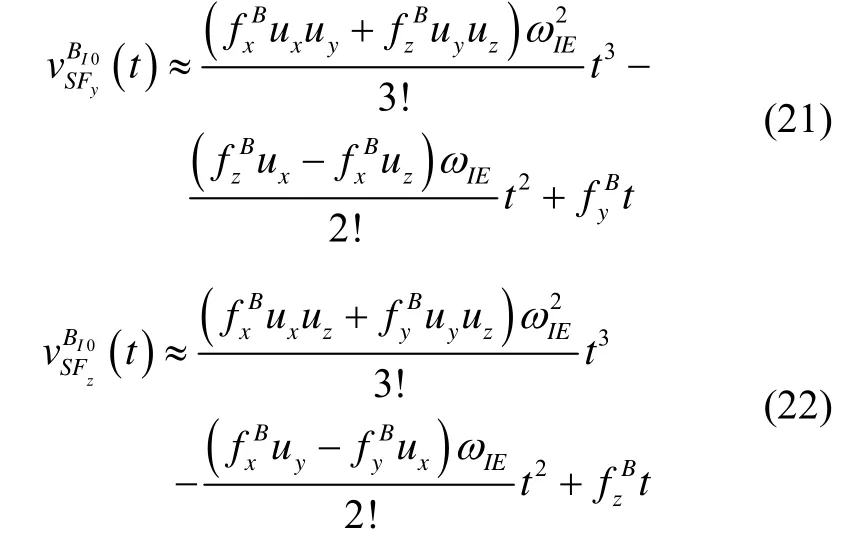
因此,可以采用多項式擬合。
為驗證上述推到與數學仿真的吻合程度,不失一般性假設在進行對準時初始載體系與當地水平系重合,XY軸水平,有:
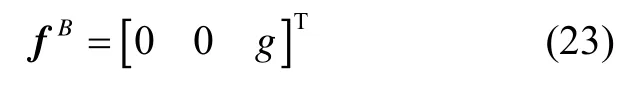
因此,
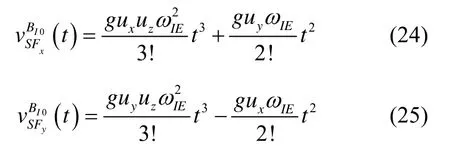

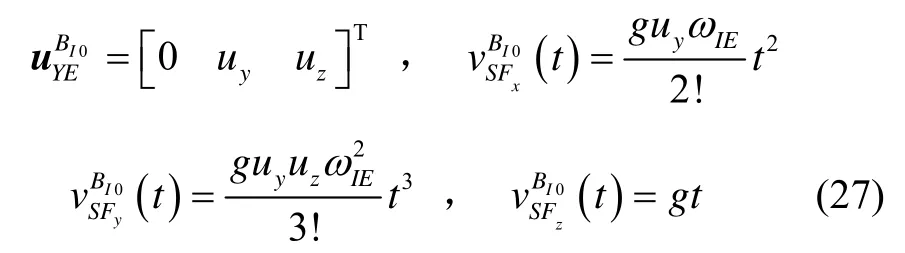
3 仿真分析
為了驗證上述多項式擬合分析的正確性,進行數據仿真分析。
3.1 無器件誤差的仿真
設慣性器件無誤差,進行慣性系對準仿真計算,并實時輸出解算中間數據,初始體坐標系與導航系重合,仿真計算時長為30 s。
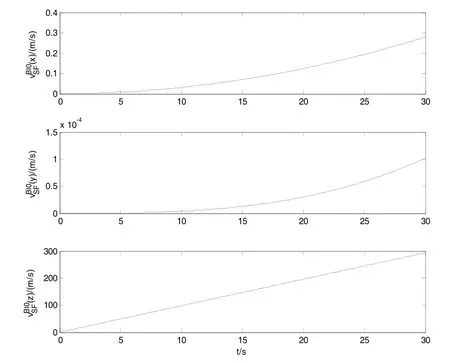
圖1 視速度計算值Fig.1 Calculated values of specific velocity
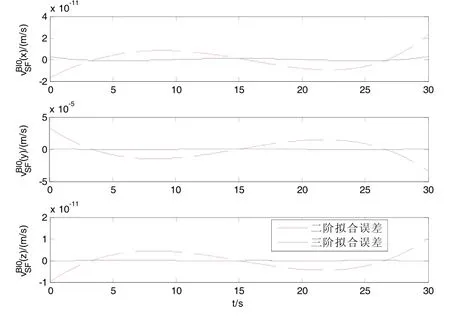
圖2 視速度擬合誤差Fig.2 Fitted values of specific velocity
為充分分析上述擬合對對準結果的影響,分別采用一階、二階、三階、四階擬合進行對準仿真,仿真結果如表1所示(方位真值為270°)。
從表1中可以看出,在無器件誤差的情況下無需擬合,采用一階和二階擬合對對準精度有影響,采用三階、四階不影響對準精度。
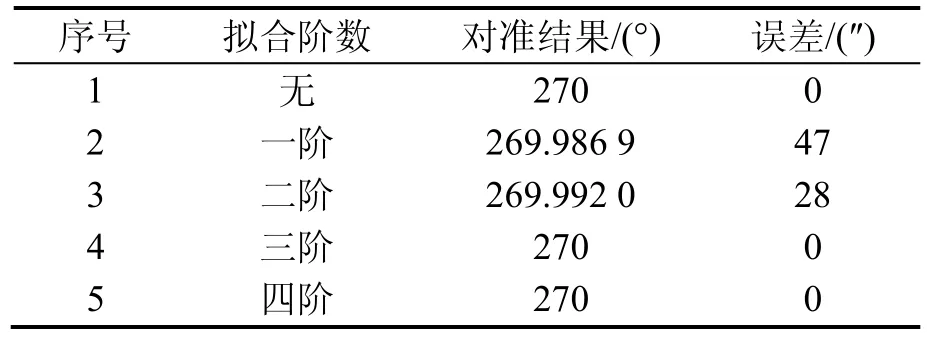
表1 無誤差不同擬合階數對準結果Tab.1 Fitted results without IMU error
3.2 含器件常值誤差的仿真
仿真用器件常值誤差如表2所示。加入上述條件的器件常值誤差后,仿真結果如表3所示。
從表2~3中可以看出,在僅包含常值誤差時,三階、四階擬合的對準結果與無擬合的效果相當,一階、二階擬合對對準精度有影響,誤差有抵消的作用,為了更真實地反映擬合效果,需進行含器件隨機誤差和振動環境的仿真。

表2 常值誤差參數表Tab.2 IM U constant error
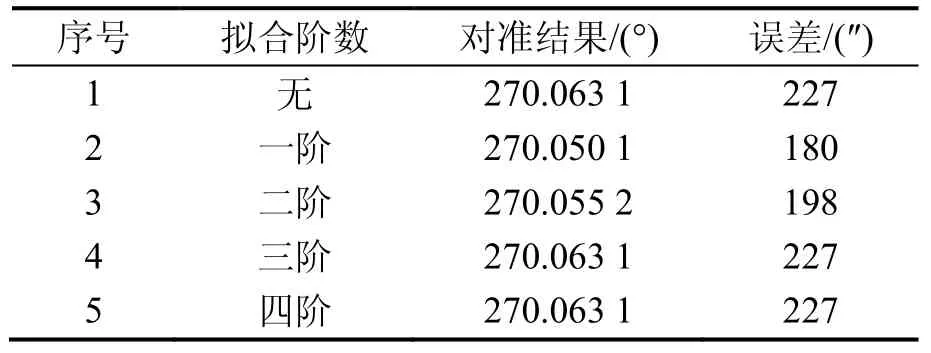
表3 常值誤差不同擬合階數對準結果Tab.3 Fitted results with constant IMU error
3.3 含器件隨機誤差的仿真
在上述常值誤差的基礎上加入隨機誤差,并進行蒙特卡洛仿真。隨機誤差如表4所示。
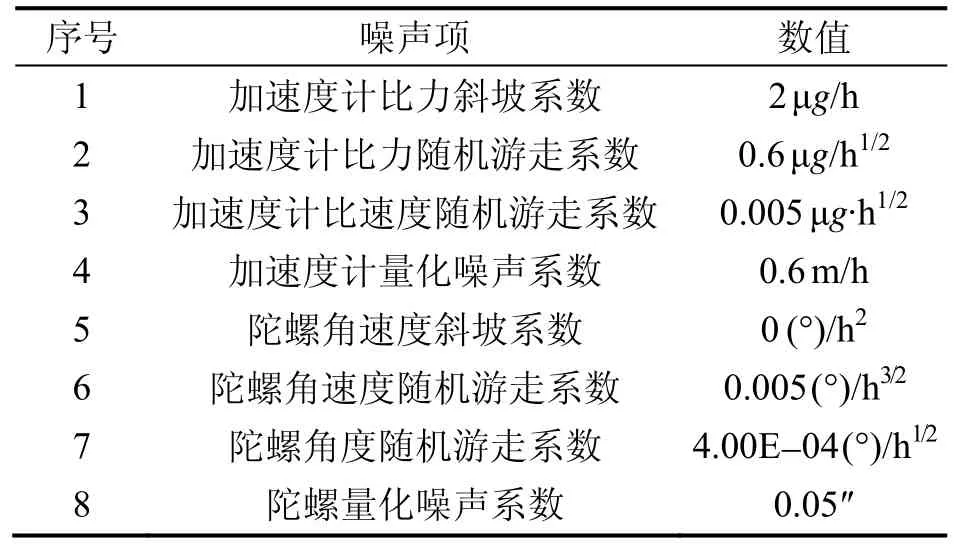
表4 隨機噪聲參數表Tab.4 IM U random noise
200次蒙特卡洛仿真如表5所示(3倍均方根)。
從表5可以看,二階及以上擬合結果明顯好于無擬合結果,驗證了該方案的可行性。
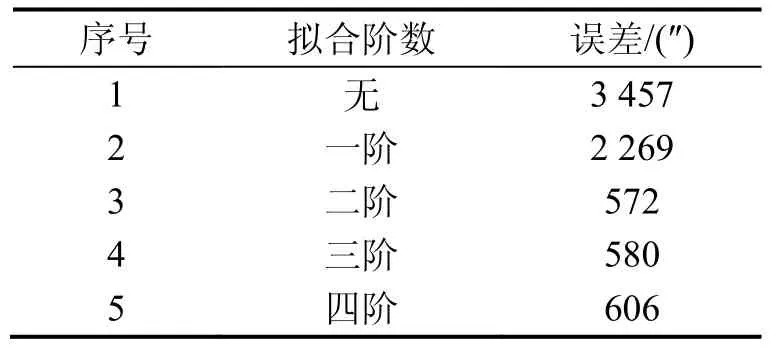
表5 蒙特卡洛仿真不同擬合階數對準結果Tab.5 Fitted results with Monte Carlo
3.4 振動環境的仿真
為了能仿真分析該方案在振動條件下的效果,將某型號慣組在試驗車上采集的靜態數據進行去除趨勢項的噪聲提取,將噪聲加入上述仿真器件輸出進行對準仿真,仿真結果如表6所示(3倍均方根)。
從表6可看出該方案的有效性,二階及以上階次的擬合相對于無擬合方案的精度提升了一個數量級。
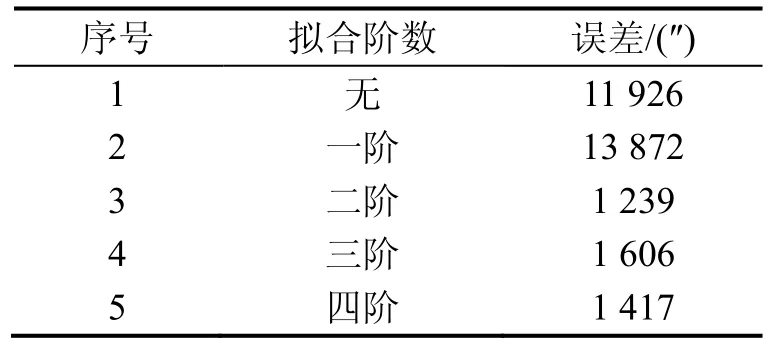
表6 振動仿真不同擬合階數對準結果Tab.6 Fitted results with vibration noise
4 測試試驗驗證
為了驗證該方案在工程中的應用效果,通過實際慣組進行測試驗證,驗證內容包括靜態對準測試、動態對準測試。
4.1 靜態對準測試
采集某型號用慣組在大理石平臺上的8 h數據,利用各對準時間段(30 s)的數據進行對準離線分析,求取多個對準簇對準結果的穩定性(3倍標準差),結果如表7所示。
從表 7可以看出,采用二階、三階、四階擬合效果相差不大,比不采用擬合及一階擬合的穩定性要好很多。上述試驗結果表明,在沒有振動干擾的條件下,僅器件噪聲也能對慣性系對準精度產生影響,導致對準精度降低,通過采用擬合的方法可以有效提升對準精度。
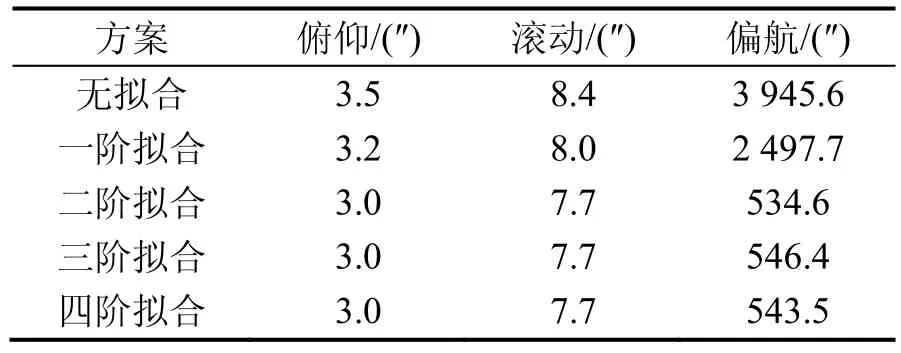
表7 靜態對準穩定性測試結果Tab.7 Fitted results with static test
4.2 動態對準測試
將某型號慣組放置在專用試驗車上進行動態對準測試,開啟車輛的底盤發動機和設備供電發電機,中途有人員上下車,共進行6個不同方位的試驗,每個方位進行8次試驗,每次對準時間為30 s,每次試驗結束后靜止1 min,統計8次試驗的穩定性(3倍標準差),以此判斷對準精度。不同方位在不同擬合方案下的結果如表8所示。
從表8可以看出,在慣組處于振動情況時,不進行擬合處理的慣性系對準將出現較大誤差,最大約17°,明顯超出振動幅度,當進行二階以上擬合后,最大約2.5°,精度提升明顯。上述試驗結果表明,基于多項式擬合的抗干擾慣性系粗對準算法能有效抑制外界振動環境帶來的比力干擾。
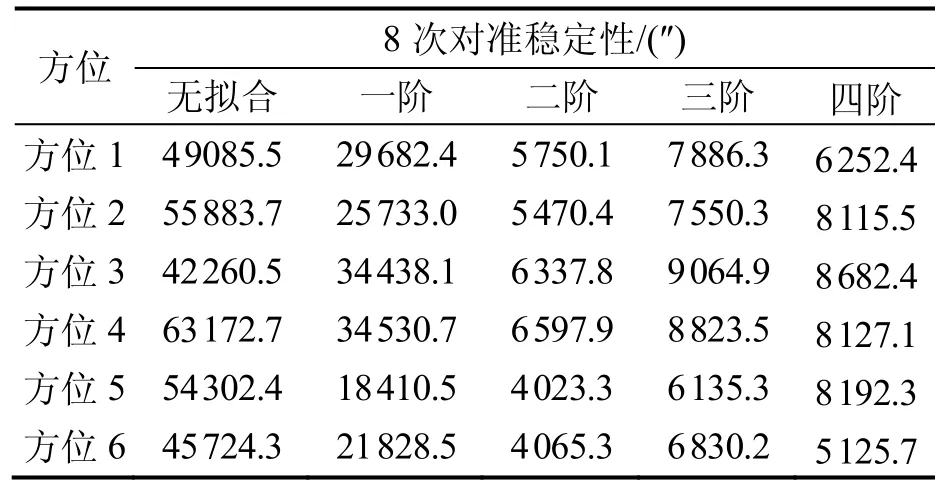
表8 動態對準穩定性測試結果Tab.8 Fitted results with dynamic test
5 結 論
慣性系對準能較好地解決了振動條件下的對準問題,在實際工程中得到了廣泛應用,但在以離散化方式計算BI0系下視速度時,容易因慣性器件偏差及擾動帶來的加速度干擾信息導致輸出不穩定,影響對準結果。本文在詳細分析慣性系對準中視速度解算方法的基礎上,提出了利用多項式擬合的分析方法。詳細分析了擬合階次,并進行了仿真分析和實物測試驗證。仿真及測試結果表明,相比于不進行擬合的傳統方案,該方案能明顯提升對準精度。
(References):
[1]Liu X X, Zhao Y, Liu X J, et al.An improved self- alignment method for strapdown inertial navigation system based on gravitational apparent motion and dual-vector[J].Review of Scientific Instruments, 2014, 85(12): 125108.
[2]徐曉蘇, 劉心雨.一種改進的粒子濾波算法在SINS初始對準中的應用[J].中國慣性技術學報, 2016, 24(3): 299-305.Xu X S, Liu X Y.Improved particle filter algorithm in SINS initial alignment[J].Journal of Chinese Inertial Technology, 2016, 24(3): 299-305.
[3]Li J, Xu J, Chang L, et al.An improved optimal method for initial alignment[J].Journal of Navigation, 2014,67(4): 727-736.
[4]王志偉, 秦俊奇, 楊功流, 等.炮載捷聯慣導晃動誤差補償方法[J].中國慣性技術學報, 2017, 25(1): 37-42.Wang Z W, Qin J Q, Yang G L, et al.Compensation method for vehicle-body shaking errors of gun-board SINS[J].Journal of Chinese Inertial Technology, 2014, 67(4): 727-736.
[5]Liu Y H, Liu M Y, Teng H J, et al.Anti-jamming alignment method for rotary RLG SINS[J].Journal of Chinese Inertial Technology, 2012, 20(6): 654-657.
[6]崔鵬程, 鄒志勤, 王翌, 等.桿臂效應誤差對晃動基座粗對準的影響[J].中國慣性技術學報.2013, 21(4): 462-466.Cui P C, Zou Z Q, Wang Y, et al.Influence of lever-arm effect error on coarse alignment on shaking base[J].Journal of Chinese Inertial Technology, 2013, 21(4): 462-466.
[7]Liu X J, Li Y T.Fast alignment algorithm of inertial fixed frame in quasi-static environment[J].Journal of Chinese Inertial Technology, 2014, 22(4): 459-462.
[8]Wang R Y, Liu W C, Bian H W, et al.Fast alignment algorithm with order-reduced filter for SINS[J].Journal of Chinese Inertial Technology, 2016, 24(5): 607-618.
[9]Li Q, Ben Y Y, Sun F.A novel algorithm for marine strapdown gyrocompass based on digital filter[J].Measurement, 2013, 46(1): 563-571.
[10]黃鳳榮, 高峰, 付中澤, 等.基于小波濾波的激光陀螺SINS晃動基座初始對準[J].中國慣性技術學報, 2014,22(2): 157-160.Huang F R, Gao F, Fu Z Z, et al.Wavelet used in initial alignment of SINS on a rocking base[J].Journal of Chinese Inertial Technology, 2014, 22(2): 157-160.
[11]Qin F J, Li A, Xu J N.Improved fast alignment method of strapdown INS using bidirectional processes and denoising[J].Journal of Chinese Inertial Technology,2014, 22(4): 453-458.
[12]趙長山, 秦永元, 魏亮.抗干擾重力加速度積分粗對準算法[J].宇航學報, 2010, 31(10): 2335-2339.Zhao C S, Qin Y Y, Wei L.A gravity-based antiinterference coarse alignment algorithm[J].Journal of Astronautics, 2010, 31(10): 2335-2339.
Anti-disturbance inertial-frame alignment algorithm based on polynomial fitting
HU Hua-feng, LIU Ming, LI Dan
(Overall Designing Institute of Hubei Space Technology Academy, Wuhan 430040, China)
Inertial-frame alignment accuracy will be affected by various specific-force-disturbing factors such as gusts of wind, vehicle vibration, loading, offloading, and sensor noise.To solve this problem, the reference vectors used in inertial-frame alignment is deducted and analyzed, and then a polynomial fitting method is proposed.The method fits the specific velocity within the whole alignment duration by polynomials, and uses the fitted vectors instead of the original cyclic-calculated vectors which are easily disturbed.Simulation and experiment results show that the new method can accomplish the alignment with higher precision.The alignment accuracy of INS is improved by more than 7 times.In addition, the new method can be easily applied in engineering.
disturbance; inertial frame; polynomial fitting; initial alignment
V249.3
A
1005-6734(2017)05-0571-05
10.13695/j.cnki.12-1222/o3.2017.05.003
2017-05-14;
2017-08-18
武器裝備“十三五”預研資助(30401020402)
胡華峰(1986—),男,工程師,主要從事慣性技術研究。E-mail: h-hfeng@163.com

