車輛動力學(xué)模型輔助的慣性導(dǎo)航系統(tǒng)

張月新，王立輝，湯新華

（東南大學(xué) 儀器科學(xué)與工程學(xué)院微慣性儀表與先進導(dǎo)航技術(shù)教育部重點實驗室，南京 210096）

車輛動力學(xué)模型輔助的慣性導(dǎo)航系統(tǒng)

張月新，王立輝，湯新華

（東南大學(xué) 儀器科學(xué)與工程學(xué)院微慣性儀表與先進導(dǎo)航技術(shù)教育部重點實驗室，南京 210096）

為提高車輛導(dǎo)航系統(tǒng)的精確度和可靠性，提出一種車輛動力學(xué)模型輔助慣性導(dǎo)航系統(tǒng)的方法。建立車輛非線性動力學(xué)模型，利用四階龍格庫塔法實時解算速度信息。以慣導(dǎo)誤差方程為狀態(tài)方程，動力學(xué)模型與慣性導(dǎo)航解算的速度差為觀測量，設(shè)計了容積卡爾曼濾波器，并用估計的狀態(tài)誤差對慣導(dǎo)進行校正。仿真結(jié)果表明，所提出的利用車輛動力學(xué)模型輔助慣導(dǎo)的方法能有效抑制慣導(dǎo)誤差的發(fā)散，位置精度和速度精度比純慣導(dǎo)系統(tǒng)提高了一個數(shù)量級，航向角精度提高了73%。

慣性導(dǎo)航系統(tǒng)；車輛動力學(xué)模型；容積卡爾曼濾波；組合導(dǎo)航

慣性導(dǎo)航系統(tǒng)（Inertial navigation system, INS）具有信息量豐富、自主性等優(yōu)勢，但INS導(dǎo)航誤差隨時間積累，無法長時間單獨定位[1]。衛(wèi)星導(dǎo)航系統(tǒng)用于輔助 INS應(yīng)用最廣，但自主性差，在其失效階段，組合導(dǎo)航系統(tǒng)只能依賴INS工作，無法保證車輛導(dǎo)航系統(tǒng)長時間工作的精度[2-3]。而車輛動力學(xué)模型（Vehicle dynamic model, VDM）對載體狀態(tài)估計，不需依賴外部條件，具有較強的自主性和適用性[4]，可以利用VDM有效地輔助INS進行導(dǎo)航。

目前，基于VDM的車輛狀態(tài)估計主要有兩類，一類是以速度為已知量，利用非線性VDM對側(cè)偏角等狀態(tài)進行估計[5-6]，該類方法對速度的精度要求較高。第二類是以輪胎力為已知量，基于擴展卡爾曼濾波器、一階斯梯林插值濾波器、遞推最小二乘法濾波器，估計車速、橫擺角速度、質(zhì)心側(cè)偏角等狀態(tài)[7-9]。但第二類方法中將非線性模型簡化為線性時會造成一定的誤差，降低測量精度，并且VDM估計的狀態(tài)信息沒有用于輔助其他導(dǎo)航系統(tǒng)，具有一定的局限性。

針對第二類方法的不足，基于容積卡爾曼濾波器（cubature Kalman filter, CKF）提出VDM輔助INS的組合導(dǎo)航方法。建立車輛三自由度非線性動力學(xué)模型，利用四階龍格庫塔法實時解算速度信息。以 INS誤差方程為狀態(tài)方程，VDM與INS解算的速度差為觀測量，設(shè)計了CKF，并用估計的狀態(tài)誤差對INS進行反饋和輸出校正。該方法中所采用的CKF算法無需對狀態(tài)模型線性化，直接通過非線性系統(tǒng)方程對容積點進行傳播，估計精度高。VDM輔助INS的組合導(dǎo)航方法可有效抑制INS導(dǎo)航誤差發(fā)散，改善車輛導(dǎo)航系統(tǒng)的可靠性。

1 VDM輔助INS的組合導(dǎo)航系統(tǒng)模型

基于CKF的VDM輔助INS的組合導(dǎo)航系統(tǒng)如圖1所示，INS根據(jù)微慣性器件輸出的角增量和比力，利用姿態(tài)更新、速度更新和位置更新算法解算車輛的姿態(tài)、速度和位置；VDM 以方向盤轉(zhuǎn)角和縱向力為輸入量，利用四階龍格庫塔法實時解算載體坐標(biāo)系的速度，根據(jù)INS得到的姿態(tài)矩陣轉(zhuǎn)換為導(dǎo)航坐標(biāo)系下的速度；設(shè)計了CKF，以INS和VDM測量的速度之差作為觀測量，INS的誤差方程為狀態(tài)方程，估計INS狀態(tài)誤差，并用估計狀態(tài)誤差對INS進行校正。

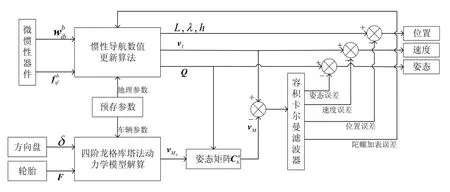
圖1 VDM輔助INS原理圖Fig.1 Schematic diagram of VDM aided INS

1.1 INS數(shù)值更新算法

INS數(shù)值更新算法利用六軸加速度計和陀螺儀測量載體的比力和角增量，根據(jù)已知的初始條件，解算出載體當(dāng)前時刻的導(dǎo)航參數(shù)。導(dǎo)航坐標(biāo)系n采用東北天地理坐標(biāo)系，載體坐標(biāo)系b采用右前上坐標(biāo)系。INS基本方程包含姿態(tài)微分方程、比力微分方程和位置微分方程。其中，姿態(tài)四元數(shù)微分表達式為

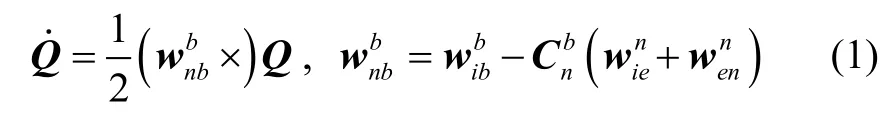
式中：Q為姿態(tài)四元數(shù)；為載體系相對于導(dǎo)航系的角速度；為陀螺輸出的載體系相對于慣性系的角速度為地球自轉(zhuǎn)引起的導(dǎo)航系旋轉(zhuǎn)角速度；為載體運動產(chǎn)生的位移角速度；為導(dǎo)航系轉(zhuǎn)換到載體系的姿態(tài)旋轉(zhuǎn)矩陣。

比力微分方程為

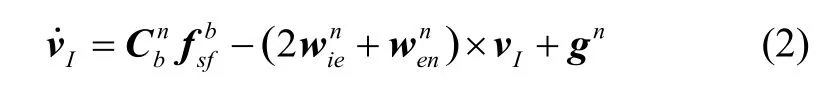
INS的位置（緯度L、經(jīng)度λ、高度h）微分方程式如下：

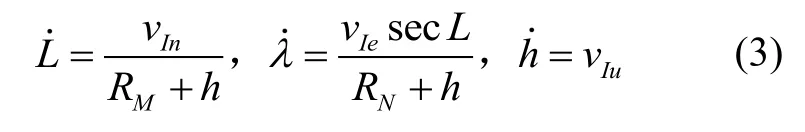
對于在路面上行駛的車輛，可以假設(shè)車輛不離開地面，則車輛在載體坐標(biāo)系下的向上速度等于0，得到其非完整約束條件為

1.2 車輛動力學(xué)模型

VDM 利用載體自身的輸入量，解算出載體的部分運動參數(shù)，如速度、角速率等。VDM 解算結(jié)果輔助校正INS的輸出，從而構(gòu)成INS/VDM的組合導(dǎo)航系統(tǒng)，提高車輛導(dǎo)航精度。建立橫向、縱向、橫擺三自由度非線性車輛動力學(xué)模型，忽略左右輪差異后模型可等效簡化為前、后車輪分別集中在車輛前、后軸中點而構(gòu)成的一個自行車模型，如圖2所示。為導(dǎo)航坐標(biāo)系，軸向東，軸向北；為固定在車輛質(zhì)心上的載體坐標(biāo)系，軸與載體橫軸重合，向右為正，軸與載體縱軸重合，向前為正。

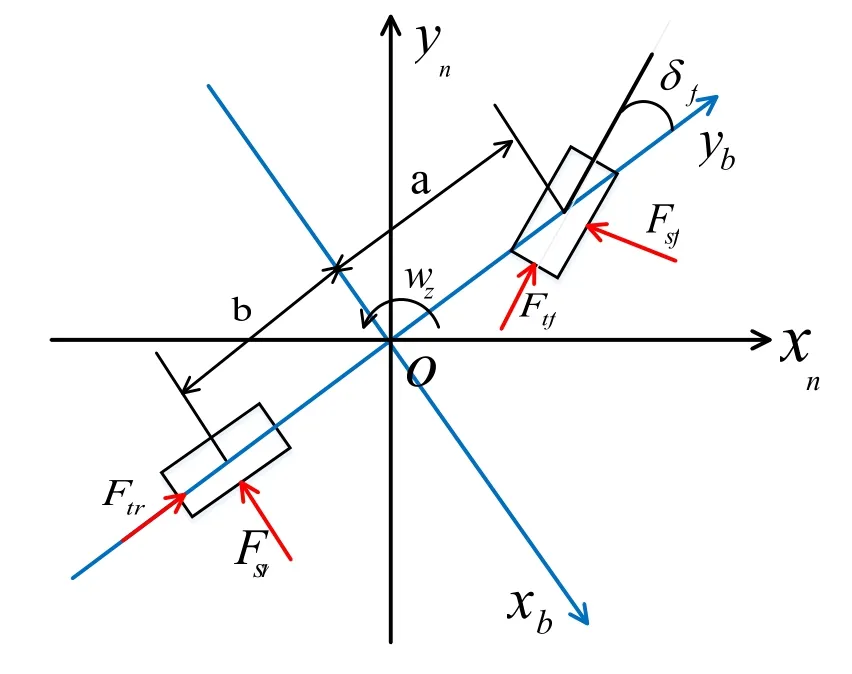
圖2 車輛動力學(xué)模型示意圖Fig.2 Schematic diagram of vehicle dynamic model

據(jù)牛頓力學(xué)，車輛的動力學(xué)模型為

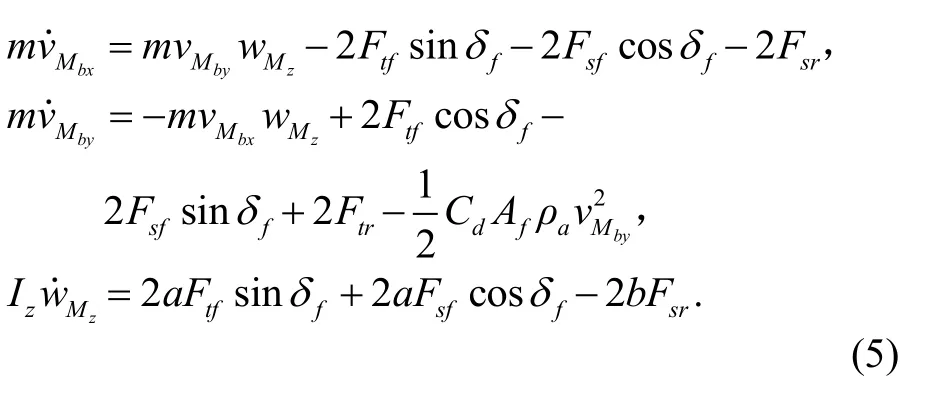
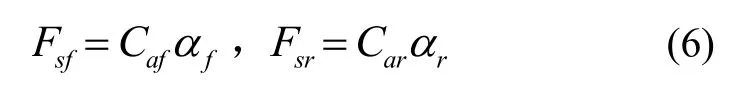
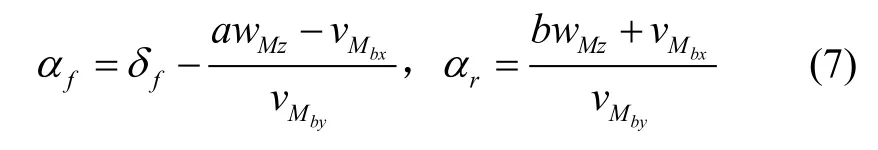
車輛大部分行駛情況下前輪轉(zhuǎn)向角小于 10°，在極限情況下前輪轉(zhuǎn)向角在30°到40°之間，為應(yīng)用方便通常可假定前輪轉(zhuǎn)向角δf為小角度。將式(6)(7)代入式(5)，并考慮到δf是小角度（即且忽略二階及以上的高階微量），經(jīng)整理后可得：

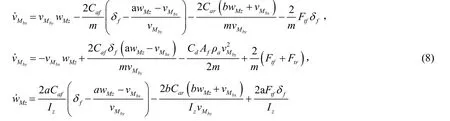
利用方向盤轉(zhuǎn)角傳感器和車輪力傳感器信息得到車輛動力學(xué)模型的控制輸入向量通過四階龍格庫塔法求解微分方程(8)可得載體坐標(biāo)系下車輛的橫向速度縱向速度和橫擺角速度根據(jù)INS解算的姿態(tài)矩陣，可得到導(dǎo)航坐標(biāo)系下由動力學(xué)模型計算的速度：

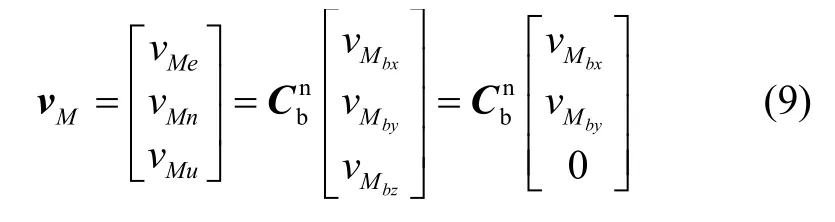
2 VDM輔助INS濾波器設(shè)計

2.1 狀態(tài)方程和量測方程

采用組合導(dǎo)航間接濾波法，綜合考慮系統(tǒng)的精度和實時性，誤差狀態(tài)變量包括3個姿態(tài)誤差、2個速度誤差、2個位置誤差、3個陀螺常值漂移、2個加速度計常值零偏，即

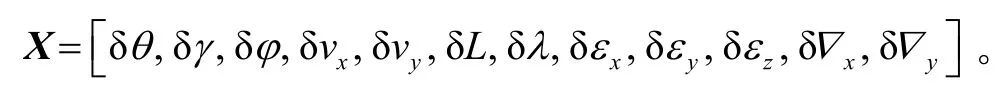
卡爾曼濾波器的狀態(tài)方程為

式中：A為相應(yīng)的狀態(tài)轉(zhuǎn)移矩陣，由INS誤差方程構(gòu)成[10]；w為過程噪聲。

將INS和VDM解算的東向速度之差、北向速度之差作為卡爾曼濾波器的觀測量，即觀測向量為則系統(tǒng)的量測方程為

對于式(10)(11)所描述的系統(tǒng)狀態(tài)方程和量測方程，對其進行離散化，得到k時刻的離散化系統(tǒng)狀態(tài)模型為

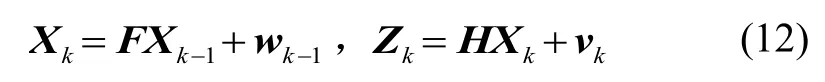
2.2 容積卡爾曼濾波器

CKF采用一組等權(quán)值的容積點解決貝葉斯濾波的積分問題，CKF算法具有很好的非線性逼近性能、數(shù)值精度以及濾波穩(wěn)定性[11]。其算法步驟如下：

① 時間更新

1）構(gòu)造容積點：

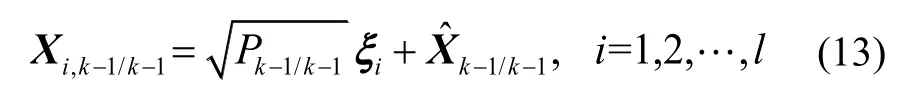
2）計算經(jīng)狀態(tài)方程傳播容積點：

德國羅斯勒公司是生產(chǎn)和銷售研磨、拋丸設(shè)備的專業(yè)廠商，主要產(chǎn)品有研磨光整系統(tǒng)和拋丸清理系統(tǒng)，包括用于發(fā)動機、起落架以及機翼等部件的光飾產(chǎn)品和拋丸設(shè)備，適于軸類、盤類和葉片的應(yīng)力強化與拋丸處理。羅斯勒公司創(chuàng)立于1933年，其表面處理技術(shù)居世界領(lǐng)先地位，目前已在英國、法國、西班牙、意大利、比利時、奧地利、新加坡、巴西、南非和美國等國家設(shè)有分公司，并計劃在中國投資建廠。

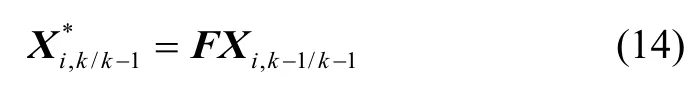
3）一步預(yù)測狀態(tài)和誤差協(xié)方差陣：

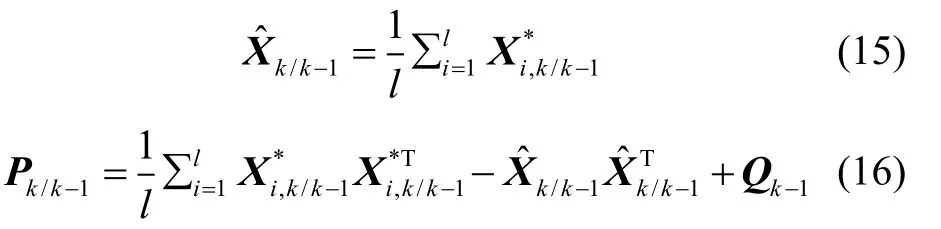
② 量測更新

1）構(gòu)造容積點：

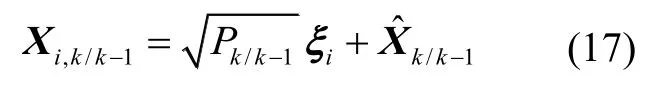
2）計算經(jīng)量測方程傳播容積點：

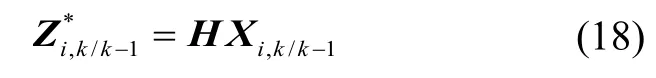
3）計算觀測量預(yù)測值：

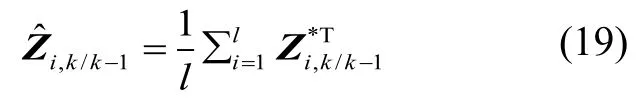
4）估計新息自協(xié)方差矩陣：

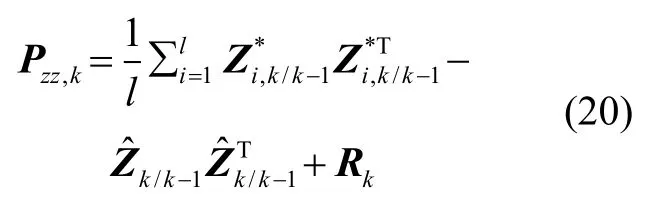
5）估計互協(xié)方差矩陣：

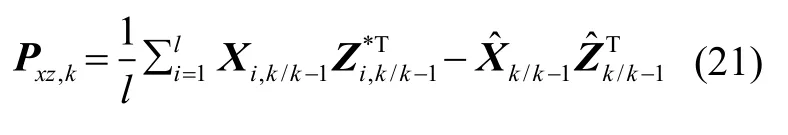
6）卡爾曼增益矩陣：

7）估計k時刻的狀態(tài)量：

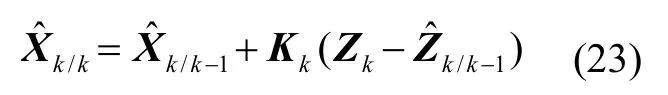
8）估計k時刻狀態(tài)誤差協(xié)方差陣：

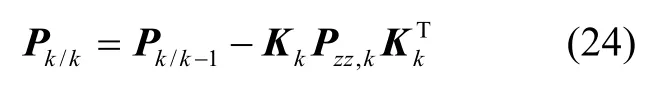
3 仿真驗證與分析

Carsim仿真中設(shè)置汽車的方向盤轉(zhuǎn)角δ按幅值 60°的正弦規(guī)律變化，汽車的縱向速度在不斷的加速、勻速和減速變化，方向盤轉(zhuǎn)角和縱向速度隨時間的變化過程如圖3所示，仿真時長為120 s，采樣時間為0.01 s。在不考慮外界因素變化的情況下，對于確定的車輛，參數(shù)都是固定的，這些參數(shù)不會隨著車輛的行駛而變化。當(dāng)外界因素變化（如車輛的負(fù)載變化引起質(zhì)量m、Iz的變化）時，若將參數(shù)m、Iz當(dāng)作常量，會影響測量精度，此時可根據(jù)實際需求，增加測量m的傳感設(shè)備，通過四階龍格庫塔法求解微分方程(8)時利用實時更新的參數(shù)m、Iz，可以保證車輛導(dǎo)航的精確性。仿真實驗車輛是一個前輪轉(zhuǎn)向的四輪車，不考慮外界因素的變化，其主要參數(shù)如下：

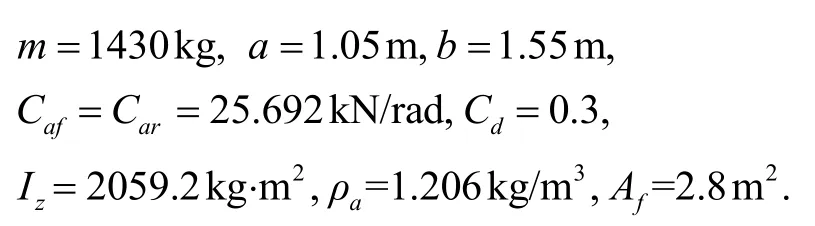
方向盤傳動比為 20。設(shè)定車輛動力學(xué)模型中 3個外輸入傳感器的量測噪聲為均值是0，方差分別為0.5°、20 N、20 N的高斯白噪聲。初始緯度為32.0586°，經(jīng)度為118.7869°，高度為0 m，初始速度和姿態(tài)為零，陀螺常值漂移為0.01 (°)/s，角度隨機游走為加速度計常值漂移為速度隨機游走為

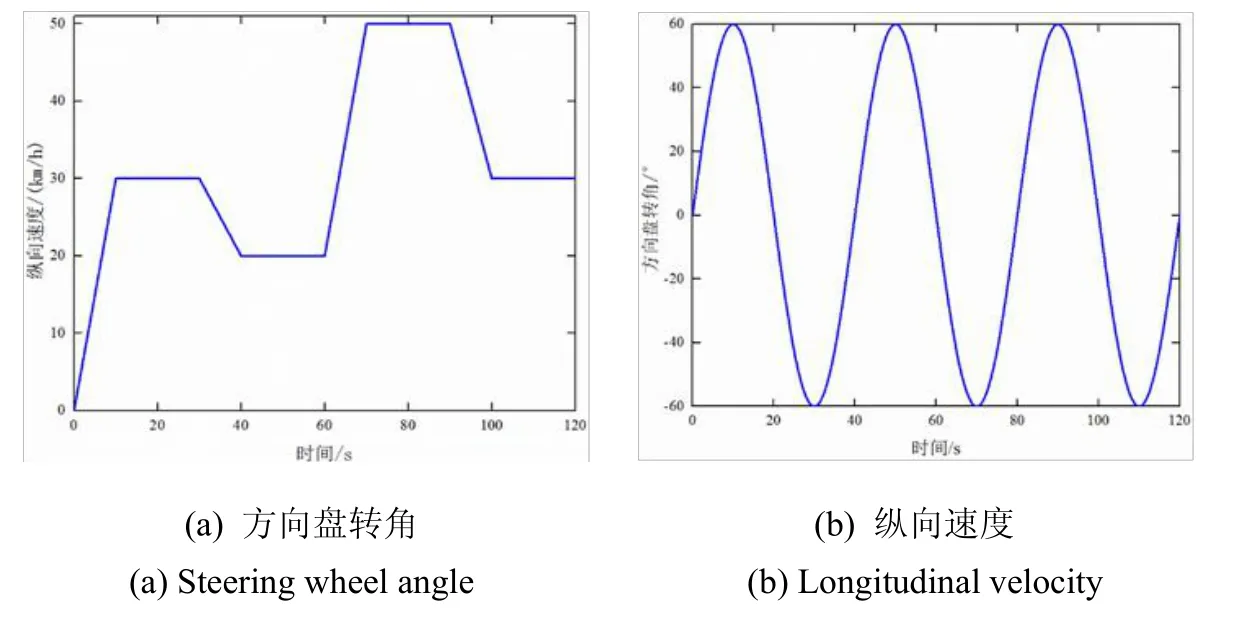
圖3 Carsim仿真設(shè)置Fig.3 Simulation settings of Carsim

根據(jù)上述設(shè)置，對INS和INS/VDM組合導(dǎo)航進行數(shù)值仿真研究，仿真結(jié)果如圖4～6所示。其中標(biāo)注為“真實值”的曲線表示真實結(jié)果，標(biāo)注為“INS”的曲線表示純慣性導(dǎo)航系統(tǒng)解算的結(jié)果，標(biāo)注為“INS/VDM”的曲線表示動力學(xué)輔助導(dǎo)航系統(tǒng)修正解算的結(jié)果。圖4中分別是經(jīng)度、緯度和行駛軌跡的對比圖。可以看出，運行30 s后INS測量的經(jīng)度偏離真實值增大，120 s時間內(nèi)經(jīng)度的最大偏差為0.43′，緯度最大偏差為0.15'。INS/VDM組合導(dǎo)航的運行軌跡和真實軌跡吻合度高，經(jīng)度、緯度的最大偏差分別為0.006′和0.01′。圖5中分別為東向速度和北向速度的導(dǎo)航速度對比圖，INS測量的東向速度偏差較大，經(jīng)INS/VDM組合導(dǎo)航改善后，最大東向速度誤差由14.7 m/s降低到0.6 m/s，最大北向速度誤差由8.52 m/s降低到0.84 m/s。從圖6航向角對比圖可以看出，最大航向角誤差降低了78.4%。VDM輔助INS的組合導(dǎo)航方法在位置、速度和姿態(tài)上均有明顯的改善效果。表1給出了INS精度和INS/VDM組合導(dǎo)航系統(tǒng)精度的對比。

由表1可以看出，由于采用的慣性器件精度較低，純慣導(dǎo)系統(tǒng)誤差發(fā)散快，INS/VDM 組合導(dǎo)航系統(tǒng)估計的位置和速度精度比INS提高一個數(shù)量級，航向角估計精度提高了73%。VDM輔助INS對INS誤差的發(fā)散有很好地抑制效果。

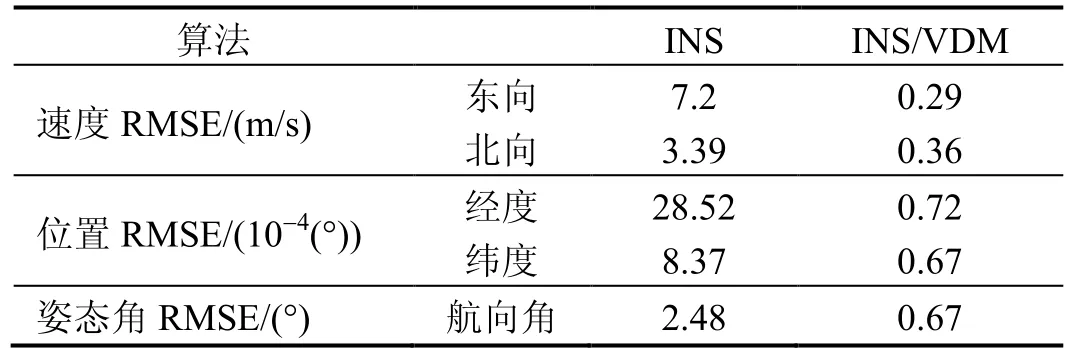
表1 INS和INS/VDM精度對比Tab.1 Comparison on precisions of INS and INS/VDM

圖4 導(dǎo)航位置對比Fig.4 Comparison of navigation positions

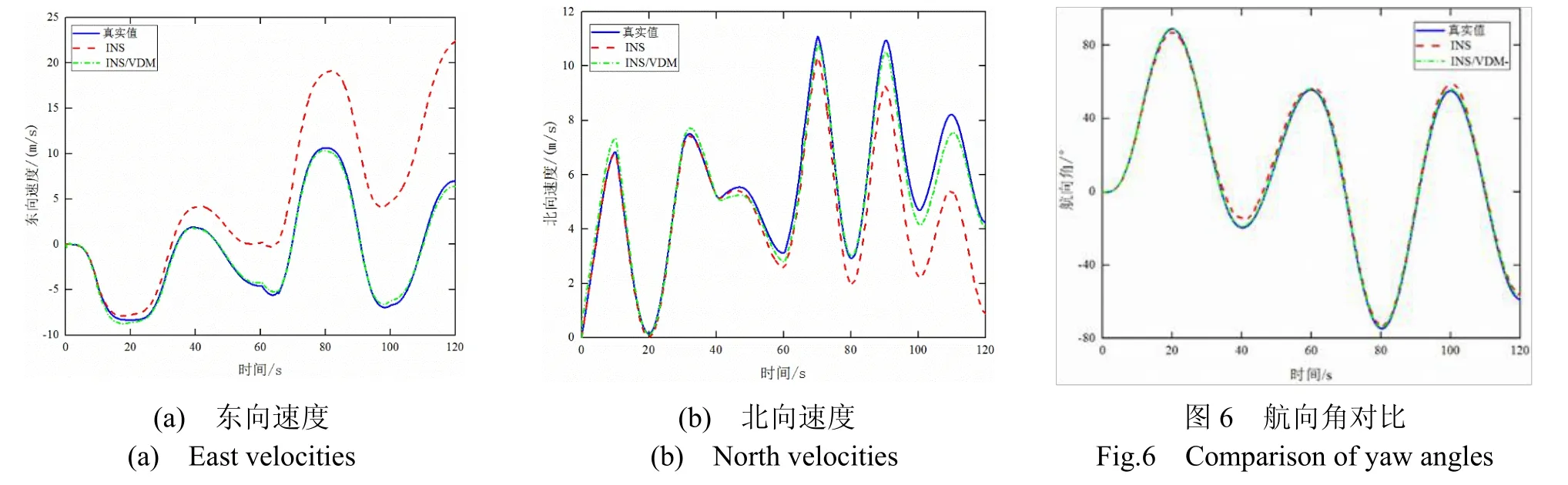
圖5 導(dǎo)航速度對比Fig.5 Comparison of navigation velocities

4 結(jié) 論

針對INS導(dǎo)航誤差隨時間積累，無法長時間保持導(dǎo)航精度的問題，研究了一種基于CKF的VDM輔助INS的組合導(dǎo)航方法。VDM通過對車輛的力學(xué)分析建立車輛運動的微分方程組，采用四階龍格庫塔法對速度、角速率進行解算，自主性和實時性好，無累積誤差。組合導(dǎo)航狀態(tài)模型的觀測量是VDM和INS解算的速度差，狀態(tài)方程是 INS的誤差方程，利用 CKF對狀態(tài)誤差進行估計并修正 INS。仿真結(jié)果表明，INS/VDM 組合導(dǎo)航系統(tǒng)的位置精度和速度精度比INS提高了一個數(shù)量級，航向角精度提高了73%，有效地抑制了INS誤差發(fā)散，達到了提高車輛導(dǎo)航系統(tǒng)精確度和可靠性的目的。

（References）：

[1]李博文, 姚丹亞.低成本車載 MEMS慣導(dǎo)導(dǎo)航定位方法[J].中國慣性技術(shù)學(xué)報, 2014, 22(6): 719-723.Li B W, Yao D Y.Low-cost MEMS IMU navigation positioning method for land vehicle[J].Journal of Chinese Inertial Technology, 2014, 22(6): 719-723.

[2]Gao N, Zhao L.An integrated land vehicle navigation system based on context awareness[J].GPS Solutions,2016, 20(3): 509-524.

[3]Quinchia A G, Falco G, Falletti E, et al.A comparison between different error modeling of MEMS applied to GPS/INS integrated systems[J].Sensors, 2013, 13(8): 9549.

[4]Skog I, Ndel P.In-car positioning and navigation technologies: a survey[J].IEEE Transactions on Intelligent Transportation Systems, 2009, 10(1): 4-21.

[5]Li X, Song X, Chan C.Reliable vehicle sideslip angle fusion estimation using low-cost sensors[J].Measurement,2014, 51(1): 241-258.

[6]Miao Z, Zhang H, Zhang J.A robust method of vehicle stability accurate measurement using GPS and INS[J].Measurement Science Review, 2015, 15(6): 294-303.

[7]Nam K, Fujimoto H, Hori Y.Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors[J].IEEE Transactions on Vehicular Technology, 2012, 61(5):1972-1985.

[8]Lian Y F, Zhao Y, Hu L L, et al.Cornering stiffness and sideslip angle estimation based on simplified lateral dynamic models for four-in-wheel-motor-driven electric vehicles with lateral tire force information[J].International Journal of Automotive Technology, 2015, 16(4): 669-683.

[9]Kanghyun N.Application of novel lateral tire force sensors to vehicle parameter estimation of electric vehicles[J].Sensors, 2015, 15(11): 28385-28401.

[10]王麗芬, 楊功流, 單友東, 等.車載定位定向系統(tǒng)誤差在線補償方法[J].中國慣性技術(shù)學(xué)報, 2015, 23(2): 145-149.Wang L F, Yang G L, Shan Y D, et al.On-line errorcompensation of vehicular position and orientation determination system[J].Journal of Chinese Inertial Technology, 2015, 23(2):145-149.

[11]Arasaratnam I, Haykin S, Hurd T R.Cubature Kalman filtering for continuous-discrete systems: theory and simulations[J].IEEE Transactions on Signal Processing,2010, 58(10): 4977-4993.

Vehicle dynamic model aided inertial navigation system

ZHANG Yue-xin, WANG Li-hui, TANG Xin-hua
(Key laboratory of micro-inertial instrument and advanced navigation technology, Ministry of education,School of instrument science and engineering, Southeast University, Nanjing 210096, China)

To improve the accuracy and reliability of the vehicle navigation system, an inertial navigation system aided by vehicle dynamic model is proposed.A nonlinear dynamic model of the vehicle is established and a fourth-order RungeKutta algorithm is used to calculate the velocity in real time.The error equation of the inertial navigation system is the state equation, and the calculated velocity difference between the vehicle dynamic model and inertial navigation is the observation vector.Then a cubature Kalman filter is designed,and the estimated state error is used to compensate the inertial navigation system.Simulation results show that the proposed method can effectively suppress the divergence of the inertial navigation error.The accuracies of the estimated position and velocity are both one order higher than those of the pure inertial navigation system, and the accuracy of the estimated yaw angle is improved by about 73%.

inertial navigation system; vehicle dynamic model; cubature Kalman filter; integrated navigation system

V249.32

A

1005-6734(2017)05-0576-05

10.13695/j.cnki.12-1222/o3.2017.05.004

2017-05-24；

2017-08-29

國家重點研發(fā)計劃（2016YFD0702000）；國家自然科學(xué)基金（61773113，51477028，41704025）；江蘇省自然科學(xué)基金（BK20160668）

張月新（1990—），女，博士研究生，從事組合導(dǎo)航研究。E-mail: smileyuexin@163.com

聯(lián) 系 人：王立輝（1979—），男，博士生導(dǎo)師，教授，從事導(dǎo)航、精密儀器等方面的應(yīng)用研究。E-mail: wlhseu@163.com