初中數學“翻折與旋轉”問題的題型及教學策略研究

梁興安

【摘要】本文總結初中數學中出現的翻轉問題的題型與翻轉問題題型的衍生題型——旋轉問題題型，論述不同題型的教學策略。

【關鍵詞】初中數學 翻轉問題 旋轉問題 題型總結 教學策略

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2017）09A-0038-02

學數學的目的之一是將數學知識運用到實際生活當中并解決相應的問題。翻折問題和旋轉問題是比較貼近生活的，學生需要通過生活去總結這類幾何問題的規律，并且充分運用想象力，讓圖形能夠“動”起來，感受“翻折與旋轉”問題在現實生活當中的含義。

一、翻折問題

翻折問題其實質就是對稱問題，在一個平面當中，對稱問題可以分成兩大類，首先是圖形之間的對稱，通常為兩個圖形之間存在對稱關系，也可以是多項式當中的數與數關于某個基點相互對稱，這種對稱方式我們稱之為中心對稱；還有對稱方式是關于一條特定直線形成的對稱，這種對稱方式我們稱之為軸對稱。在一個較為立體的空間當中，還有兩個幾何體關于特定平面之間的對稱，但是在初中數學當中應用得不多。在初中數學中，翻折問題主要分為矩形翻折、紙片翻折、三角形翻折、圓形翻折四類問題。

（一）矩形翻折

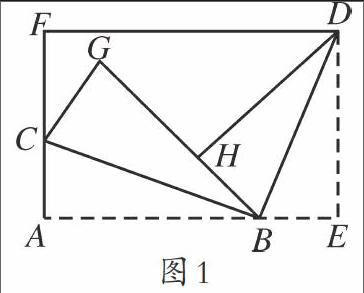
在初中數學當中，矩形的翻折問題是非常多見的，因為矩形的形體比較簡單，學生在想象時也較為容易，可變化程度也較高，因此得到了廣大出題教師的喜愛。例如：將一張長方形紙片按如圖1的方式折疊，其中BC，BD為折痕，折疊后BG和BH在同一條直線上，∠CBD= 度。

這個題目是典型的矩形翻折問題，教師在講解這個題目時，首先需要讓學生認清哪些是不變量、哪些是變量。在弄清楚兩者之后，學生對題目就會有更加深刻的認識。在這道題當中，原條件是一張長方形紙片，由BC和BD兩道折痕可以得出∠ABC與∠GBC是相等的、∠HBD與∠EBD是相等的，因此∠CBD實際上是180°的一半，即90°。教師在講解此類題目時，一定要提示學生在解題時注意每一個折疊過程當中的“變”與“不變”，理解折疊問題當中的對應邊與對應角之間的關系。

（二）紙片翻折

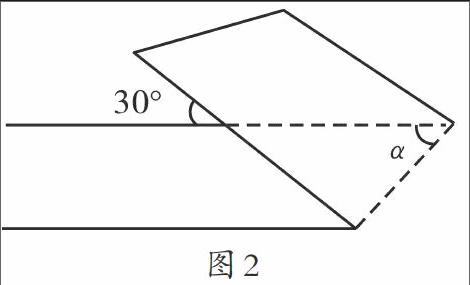
紙片翻折與矩形翻折相類似，但是不同的是紙片翻折問題更具有普遍性，它是翻折問題的精髓所在，對學生在紙片翻折問題上的概念理解有更高的要求。在初中數學當中，出題者往往根據學生已經學過的同位角、對頂角和互補角的性質來出題。例如：如圖2，有一條直的寬紙帶，按圖折疊，則∠α的度數等于（ ）。

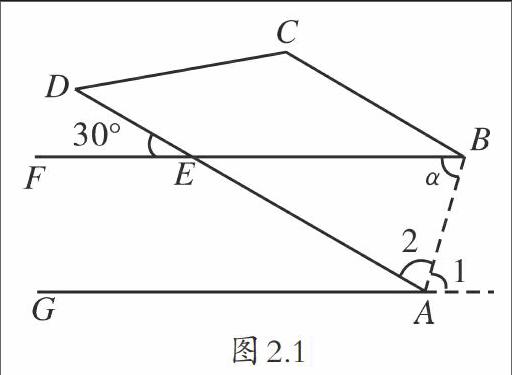
這個題目很典型地引出了紙片翻折問題，在講解這類題目時，教師可以指導學生將圖形中的點用A、B、C、D、E、F等標記出來，如圖2.1所示，學生在標記的過程中也能對題目有進一步的理解，幫助學生高效讀題；之后，教師再引導學生分析題目中給出的條件，嘗試解答。由題意可知∠DEF=30°，根據對頂角關系可知∠BEA=∠DEF=30°，同時又根據同位角關系得知∠GAE=∠BEA=∠DEF=30°，這樣就可以求出∠1=∠2=75°，再根據三角形內角和是180°求出∠α=75°。在這個題目當中，求角α的度數運用了折疊前后的不變性來解題。在初中數學的紙片翻折問題當中，這樣類型的題目占了大多數。

（三）三角形翻折

三角形作為初中數學當中常見的幾何圖形，三角形中的翻折問題也是中考的常見類型。教師在出題的時候，對于三角形的翻折問題是比較重視的，由于學生在初中數學當中已經接觸得比較多三角形了，因此在做題時比較得心應手[1]。三角形的種類較多，在實際解題中會衍生出多樣的情況，因此教師在講解三角形中的翻折問題時，應著重加強學生對已知條件的分析及對三角形自身的條件的分析能力，使得翻折問題更加明確、容易解決。

例如：如圖3，把Rt△ABC（∠C=90°）進行翻折，使A，B兩點重合，得到折痕ED，再沿BE折疊，C點恰好與D點重合，則CE：AE=_________________。

這是一個典型的與三角形相關的翻折問題，在初中數學當中也較為常見，在直角三角形ABC當中，由已知得△ADE與△BDE是關于ED對稱的，而△DBE與△CBE是關于EB對稱的。因此就可以很快得出結論，CE與ED是相等的，CB=BD=AD，再根據勾股定律來解題，假設AD=1，很快就可以得出CE與AE的比值。此題較為綜合，也是典型的勾股定理、三角形轉化與翻折相互結合的題目。

除此之外還有較為典型的探究類型的題目，例如：在△ABC中，已知∠A=80°，∠C=30°，現把△CDE沿DE進行不同的折疊得△C′DE，對折疊后產生的夾角進行探究：

①如圖4.1，把△CDE沿DE折疊在四邊形ADEB內，求∠1+∠2的和；

②如圖4.2，把△CDE沿DE折疊覆蓋∠A，則求∠1+∠2的和；

③如圖4.3，把△CDE沿DE斜向上折疊，探求∠1、∠2、∠C的關系。

根據折疊前后的圖象全等可知，∠1=180°-2∠CDE，∠2=180°-2∠CED，再根據三角形內角和定理可求出答案。諸如此類的探究題目，在題目當中往往都有固定的條件，教師在指導學生做題時，需要讓學生注意各個條件之間的關系，并且通過題目當中的條件去做一定的整改，把握好折疊的本質，這樣一來，學生解題就會游刃有余。

（四）圓形折疊

由于初中生對于圓性質的掌握還不夠熟練，因此在與圓形相關的折疊問題上可操作性不大。在初中數學當中，圓形折疊問題不常見，但是仍然需要學生掌握。

例如：如圖5，正方形ABCD的邊長為2，⊙O的直徑為AD，將正方形的BC邊沿EC折疊，點B落在圓上的F點，求BE的長。

圓形折疊問題雖然看起來比較復雜，但是越是復雜的題目實際上卻越簡單。教師在講解此題時，可首先指導學生作出輔助線如圖5.1所示，接著引導學生根據圓、三角形的特征分析圖中的邊角關系，從而得出結論。

翻折問題在初中階段多為以上幾類，除此之外，學生還需要掌握運用數形結合的方法來做題的策略，善于觀察生活當中的細微之處，聯系、分析和比較異同，這樣才能夠在解決翻折問題時不受阻撓。

二、旋轉問題

旋轉問題是初中數學當中的難點與重點，一般都是以綜合類型題目的形式出現。旋轉問題通常可以作為翻折問題的衍生題，教師應該先讓學生熟練掌握翻折問題，隨后旋轉問題自然就迎刃而解了[2]。

例如：如圖6所示，在平面直角坐標系中，O為坐標原點，點A的坐標為（-8，0），直線BC經過點B（-8，6），C（0，6），將四邊形OABC繞點O按順時針方向旋轉α°得到四邊形OA′B′C′，此時直線OA′，直線B′C′分別與直線BC相交于點P，Q。

（1）四邊形OABC的形狀是______，當α=90時，的值是______；

（2）①如圖6（b），當四邊形OA′B′C′的頂點B′落在y軸的正半軸上時，求的值；

②如圖6（c），當四邊形OA′B′C′的頂點B′落在直線BC上時，求△OPB′的面積。

這是典型的旋轉問題，在這個題目當中，可以明確地觀察到四邊形OABC旋轉后的每一個點是解題的關鍵點。教師在指導學生做旋轉類型的題目時，需要讓學生時刻抓住題目的關鍵點和關鍵步驟，弄清楚在旋轉過程當中會變化的量和不會變化的量，這樣做題才會更加地得心應手。

總而言之，隨著教育體系的進一步深化改革，貼近學生生活的翻折與旋轉問題得到了越來越多的應用。教師應該順應教育潮流、根據實際情況，幫助學生發散思維及培養創新能力，總結現階段出現的翻折和旋轉問題，讓圖形動起來，提高學生的幾何分析能力和綜合思維水平，幫助學生在未來的學習生活當中打下堅實的基礎。

【參考文獻】

[1]數學問題解決認知模式及教學理論研究[D].南京師范大學，2013.

[2]戴爾·申克著，學習理論：教育的視角[M].韋小滿等譯.南京：江蘇教育出版社，2012.

（責編 劉小瑗）endprint