小議從數學實驗的角度體會函數之美

湖北省武漢市第二高級技工學校 操先進

小議從數學實驗的角度體會函數之美

湖北省武漢市第二高級技工學校 操先進

函數是中學數學的脊梁，是整個數學教學的核心所在。中職數學中，函數教學的內容盡管并不復雜，但是對于中職生來說，函數的學習效果會深刻影響到后續(xù)數學的學習，因此教師應盡可能地在函數教學中引導學生理解和運用。從中職生現(xiàn)狀來看，如何加強其函數學習的興趣？從函數教學的哪一板塊直觀性角度切入比較好？現(xiàn)代信息技術能否合理地使用成為中職生學習的利器？這些都成為筆者函數教學的思考點。

從教材第三章第三節(jié)后的現(xiàn)代信息技術應用3——利用幾何畫板作函數圖象（靜態(tài)）這一教學內容來看，教材的設計正是努力想提高函數教學的直觀性，從函數圖象的認知出發(fā)，思考函數的變化。筆者認為，本節(jié)內容的教學時間甚至可以提前，在函數概念教學中合適給出，通過現(xiàn)代信息技術（這里主要運用教材提出的幾何畫板作為數學實驗的載體）從直觀上認知函數，從函數圖象的角度感受函數的美，通過知識與美的結合，進一步體會函數模型的重要性。

近年來，數學實驗與傳統(tǒng)教學的結合成為數學教學的新切入點。廣義上來說，一切引發(fā)學生數學學習的載體都可以稱之為數學實驗。從現(xiàn)代信息技術引入來看，數學實驗更多的是以數學軟件、計算機等實現(xiàn)數學學習的過程。要提高中職生抽象思維的能力，首先需要提升學生的學習知識興趣，幾何畫板恰恰是數學實驗入手的一款較好軟件。

案例1：繪制基本初等函數的圖象

師：請同學們找到機房電腦上的幾何畫板軟件，我們今天開始繪制各種不同的基本初等函數圖象。從初中開始，我們已經學過了一次函數、二次函數、反比例函數等等，首先請同學們繪制這幾類函數的圖象。

生：選擇幾何畫板圖表——繪制新函數——輸入新函數即可。

師：好，請在電腦上演示。

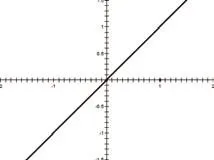
圖 1

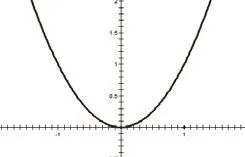
圖 2

圖3

師：好！繪制得很好。請同學們先說一說，從這三幅圖中，你所體會到的函數概念。

生：每一個自變量 都有一個因變量 與之對應。

師：從圖中你還能感受到什么？

生：第一幅圖和第三幅圖都是關于原點中心對稱，第二幅圖是關于 軸成軸對稱。

師：很好！直觀的感受，讓同學們獲得了很多獨立的思考。

意圖：從初中所學最基本的初等函數出發(fā)，引導學生回憶最常見的三個基本初等函數，從圖象直觀的角度思考函數的圖形特征，獲得了一定的感官認知。

案例2：自由繪制函數圖象

中職生對于數學的學習往往較為依賴教材，除教材之外的思考較少、摸索較少。鑒于本知識恰是開發(fā)學生發(fā)散思維的重要工具，因此筆者設計讓學生利用幾何畫板自由繪制函數圖象，并相互間展示、比較，從數學美的角度進一步認識不同的函數圖象，認識更為廣闊的函數世界，激發(fā)學生學習的興趣。

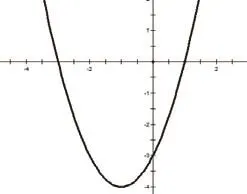
圖 4

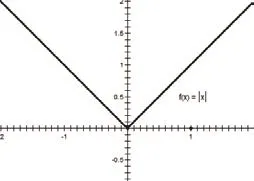
圖 5

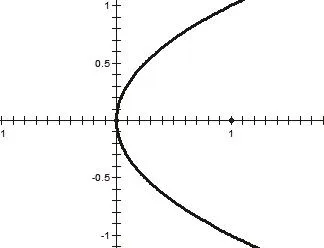
圖 6

師：請說一說你繪制的函數特點。

生：這依舊是二次函數，但是其頂點不在原點，對稱軸也不是 軸。這個二次函數圖象的對稱軸為，在 軸上的截距為，在x軸上的交點分別是

師：我們看看另一位同學用幾何畫板繪制的函數圖象。

師：好！同學們都做了嘗試，這位同學，你繪制了什么？

生：如圖6，我繪制了函數 ，跟他們的不一樣。（實驗教學的精彩時刻）

師：哦？圖象畫得很有想象力。（教師沒有想到學生會這樣畫）請大家看看，圖6和前面的五幅圖有什么不同嗎？

生：好像這個不是函數吧？（不敢確定）

師：說得很對！圖6不是函數！我們回想一下函數的概念：對于任意一個自變量，都只能有唯一的因變量與之相對應，這才是函數。而圖6中，比如取 ，則 ，顯然違背了函數的概念，因此我們只能將其稱之為曲線。

生：哦！通過對比，我們對函數的概念又有了進一步的思考。

意圖：通過自由繪制函數圖象，不僅開拓了學生的各種思路，將數學實驗運用到傳統(tǒng)教學中，還更進一步地回顧了函數的概念，使學生在動手操作中獲取知識，體現(xiàn)了數學實驗對于教學的重要作用，更理解了函數相關知識的深刻性。

案例3：與數學文化和數學美的結合

師：同學們剛剛繪制得都很好，接下來老師也給大家展示一下更有創(chuàng)意的函數或曲線。（展示圖7、圖8、圖9）同學們的視線都停留在一次函數、二次函數、反比例函數等等，其實還有很多函數有著優(yōu)美的曲線，我們將一些簡單的函數進行有效的復合，可以獲得意想不到的函數圖象。

圖 7

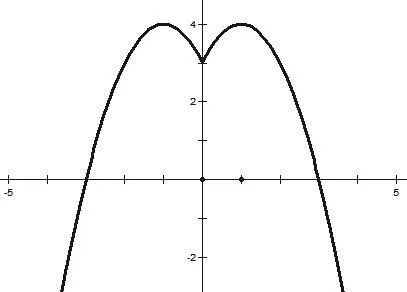
圖 8

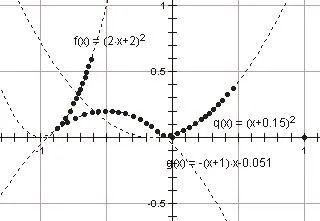
圖 9

給出三個函數解析式，請學生再次用幾何畫板進行繪制：

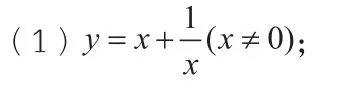
生：用幾何畫板繪制完畢，我發(fā)現(xiàn)生成了很漂亮的曲線。

師：你說說看，函數圖象給了你什么樣的感覺？

生：圖7中的上半部分我覺得非常像我們生活中的體育品牌“耐克”的標記。

生：圖8很像美國快餐品牌麥當勞的圖標。（同學們一陣歡笑）

師：是的，在開口向下的二次函數中，給自變量加上絕對值，取得了意想不到的效果！

生：圖9老師跟我們講過了，這個不是函數。有些自變量對應的因變量不是一個，看著有點像李寧的商標。

師：是的！同學們說得都非常正確。圖9的確不是函數，但是我們用充滿創(chuàng)意的變化做出了令人驚嘆的曲線，選擇一部分自變量，以分段的形式進行選取，從而獲得了“李寧”曲線。我們稍微對學過的函數進行有效的整合，創(chuàng)造了有趣的函數或曲線。

生：想不到幾何畫板給我們的函數學習帶來了這么多歡樂，課后我們再研究更為漂亮的函數。

師：希望大家用好幾何畫板，通過函數讓我們認識更多的函數圖象，了解更多的函數之美，對后續(xù)的函數運用提升自己的理解和興趣。

數學實驗對于中職生而言，是比較有效的提升學習的手段。從本課的學習來看，筆者認為有三點值得思考：第一，教學觀念的改變，中職生喜歡數學動手操作，這樣更有助于其思考積極性，傳統(tǒng)教學往往關注教師的講，導致學習效率不高；第二，幾何畫板是簡單的數學實驗軟件，其上手操作的難度不高，基本屬于所見即所得，因此受到學生歡迎；第三，要提升學習的興趣，教師要做好合理的設計，本案例既引導學生創(chuàng)造，又給出了教師的事先準備，讓課堂教學達到了一個新的高度，是學生思考的高度，可以說，學生從實驗的角度獲得了真正的體會。