拋物線(xiàn)定義的教學(xué)①

朱勝?gòu)?qiáng)

(南京外國(guó)語(yǔ)學(xué)校 210008)

1 問(wèn)題的提出

蘇教版教材對(duì)于橢圓、雙曲線(xiàn)及拋物線(xiàn)等圓錐曲線(xiàn)定義的介紹統(tǒng)一地放在“圓錐曲線(xiàn)與方程”這章的第一小節(jié)“圓錐曲線(xiàn)”中.

先讓學(xué)生直觀(guān)感知,用不同的平面截圓錐面可得到三類(lèi)不同曲線(xiàn)(如圖1),并以橢圓為例,用Dandelin雙球引導(dǎo)學(xué)生發(fā)現(xiàn)橢圓的幾何特性,形成橢圓的定義.這樣處理,便于讓學(xué)生參與到定義形成的思維活動(dòng)中來(lái),改變了以往學(xué)生只能被動(dòng)接受的局面,有利于學(xué)生更深刻地認(rèn)識(shí)橢圓.類(lèi)比橢圓得到雙曲線(xiàn)的定義也就顯得順利成章了.

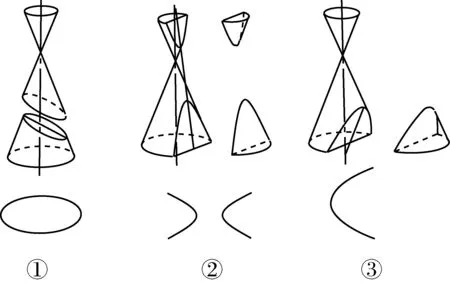
圖1

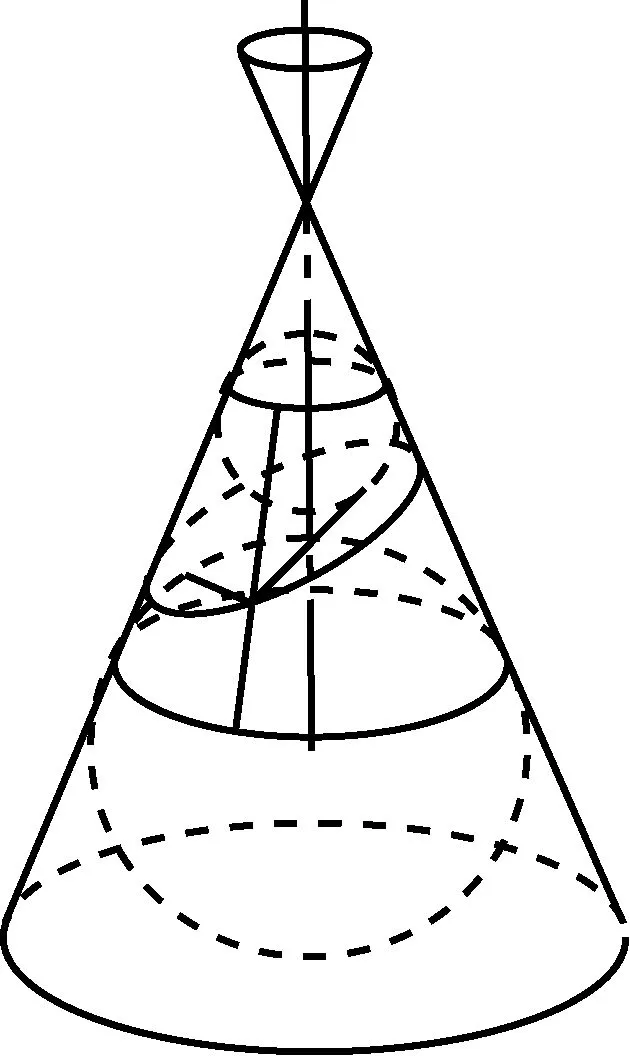
圖2

然而,教材在給出拋物線(xiàn)定義之前卻未能像橢圓那樣做充分的鋪墊.但拋物線(xiàn)又不能像雙曲線(xiàn)那樣可與橢圓進(jìn)行充分類(lèi)比.在拋物線(xiàn)定義之前,教材只有如下一段文字:

對(duì)于第三種情形(指圖1中的③),平面與圓錐曲線(xiàn)的截線(xiàn)是一條曲線(xiàn),截線(xiàn)上任意一點(diǎn)到平面內(nèi)一個(gè)定點(diǎn)的距離與一條定直線(xiàn)的距離相等.

無(wú)論是文字還是圖形,學(xué)生都無(wú)法從中看出這一幾何性質(zhì)的由來(lái).平面內(nèi)的一個(gè)定點(diǎn)是哪一點(diǎn)?一條定直線(xiàn)是哪一條直線(xiàn)?是怎么發(fā)現(xiàn)的?在獲得橢圓、雙曲線(xiàn)定義后,拋物線(xiàn)的定義卻成了學(xué)生前進(jìn)道路上的攔路虎,他們不得不等待教師的點(diǎn)撥.

許多教師也覺(jué)得拋物線(xiàn)定義的教學(xué)比較棘手,因而干脆就將定義直接告訴學(xué)生,認(rèn)為這樣做反正也不會(huì)影響后續(xù)圓錐曲線(xiàn)內(nèi)容的學(xué)習(xí).

數(shù)學(xué)教學(xué)的目標(biāo)不只是限于讓學(xué)生掌握既有知識(shí),還應(yīng)……