避開無窮 返璞歸真（上）

張景中+彭翕成

數學中的無窮，常用符號∞表示，來自于拉丁文的“infinitas”，取“沒有邊界”之義。

無窮內容之豐富，就像一個深不可測的海洋，其中不知蘊藏著多少秘密。古今中外關于無窮的著作浩如煙海。

對于無窮，數學家又愛又恨。面對無窮，常常能避則避，但避開無窮不是一件容易的事情。

1.《幾何原本》中的無窮

歐幾里得《幾何原本》中第五公設就涉及無窮。敘述如下：

如圖1，如果一條線段與兩條直線相交，在某一側的內角和小于兩直角的和，那么這兩條直線在不斷延伸后，會在內角和小于兩直角和的一側相交。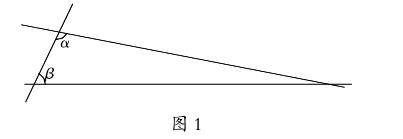

這里“不斷延伸”的字句，已經涉及無窮。

“由圓外一點P向⊙O作切線”，現在常見的的作圖法如圖2，連接OP，作OP中點M，以M為圓心，MO為半徑作圓，交⊙O于N，則PN即為所求作的切線。

而《幾何原本》中的作圖法如圖3，連接OP，交⊙O于A，過A作OP的垂線，交以O為圓心，OP為半徑的圓于點B，連接OB，交以O為圓心，OA為半徑的圓于點C，則PC即為所求作的切線。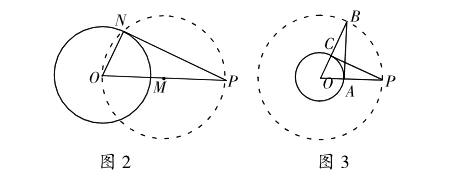

為什么《幾何原本》中不采用圖2的簡單作法呢？因為圓的直徑所對的圓周角為直角，是由三角形內角和等于180毅推導得到的。使用圖3的作法，就是希望避開平行公設，也就是避開無窮。

素數有無窮多個，在《幾何原本》中的說法卻是“質數比任意給定的一群質數還多”。注意這里避開了無窮。

2.從有限到無窮———三角形內角和定理的證明

理解無窮，要從有窮開始。

研究表明：通過驗證一個三角形的內角和為180毅，就能斷言所有三角形的內角和都為180毅！

問題一共涉及10個變元。……